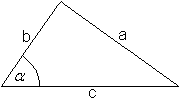
Was ist die Tangensfunktion?
Die Bezeichnung „Tangens“ führte der Mathematiker Thomas Fincke (1561–1656) in seinem Buch Geometriae rotundi (1583) ein. Quelle: http://www-history.mcs.st-andrews.ac.uk/Biographies/Fincke.html Tangenswerte
für spitze Winkel top
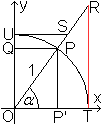
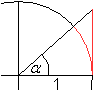
Herleitung Nach dem 2.Strahlensatz gilt AB:PQ=OA:OQ oder AB=PQ*OA:OQ=(y*1):x=y:x=tan(alpha). Man kann so leicht einsehen, dass tan(0°)=0 ist und dass tan(alpha) über alle Grenzen geht, wenn alpha sich 90° nähert. Das heißt, dass tan(90°) nicht definiert wird. Die Stelle alpha=90° ist eine Polstelle. Weiter ist zu vermuten, dass die Tangenswerte stetig mit zunehmendem Winkel monoton steigen. Genaueres ergibt sich aus den folgenden Überlegungen. Bestimmte Tangenswerte erhält man über spezielle Dreiecke.
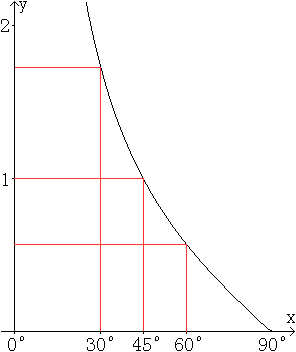
Die Zahlen lassen sich in einer Wertetabelle zusammenfassen.
Wurzelterme bzw. irrationale Zahlen als Funktionswerte sind Ausnahmen. Im Allgemeinen sind die Tangenswerte transzendente Zahlen, die angenähert als Dezimalbrüche angegeben werden können, dann aber in beliebiger Genauigkeit. Diese werden über konvergente Reihen gewonnen. Es ist heute kein Problem, sich gerundete Tangenswerte über den Taschenrechner zu verschaffen. Man bestimmt z.B. tan(30°) mit dem TI 30 über die Tastenfolge (3) (0) (TAN). Es ergibt sich tan(30°)=0,577350269. Es ist allerdings sinnlos, alle 9 Dezimalen vom Rechner zu übernehmen. Das ist zu genau, denn der Winkel ist nur auf zwei Ziffern genau vorgegeben. Nach einer Faustregel genügen dann beim Tangenswert auch zwei geltende Ziffern, tan(30°)= 0,58. Es ist aber üblich, den Tangenswert auf vier Dezimalen genau zu runden. Dazu gehört dann eine Winkelgenauigkeit von etwa 1'=1/60°. Es heißt also tan(30,0°)=0,5774. Für Winkel größer als 45° und vor allem für Winkel nahe an 90° verwendet man besser den Begriff der geltenden Ziffern. So ist z.B. laut Taschenrechner tan(88°)=28,63625328. Das sind 10 geltende Ziffern. Da sollte man auf 4 geltende Ziffern runden. Das bedeutet tan(88°)=28,64. Mit dem Taschenrechner kann man sich für eine Wertetabelle weitere Werte verschaffen und einen Graphen zeichnen. Der folgende Graph entstand allerdings mit dem Programm Winplot (URL unten). 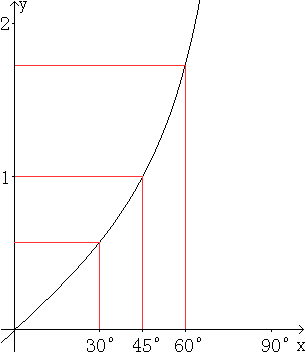 Kotangensfunktion top
Da beta=90°-alpha gilt, sehen Wertetabelle und Graph folgendermaßen aus.
Im Grunde ist die Kotangensfunktion nur eine Variante der Tangensfunktion. Tangenswerte
für weitere Winkel
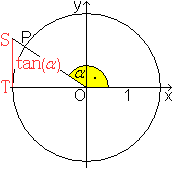
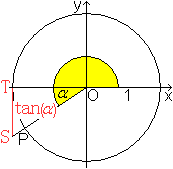
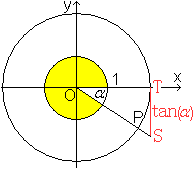
Ohne Beschränkung der Allgemeinheit kann man annehmen, dass der Punkt P auf dem Einheitskreis liegt. Auf diese Weise wird der Tangens für alle Winkel zwischen 0° und 360° erklärt. Wandert der Punkt P von der x-Achse aus entgegen dem Uhrzeigersinn weiter, so wiederholen sich die Tangenswerte: tan(alpha+360°)=tan(alpha). Berücksichtigt man die Vorzeichen, wiederholen sich die Tangenswerte schon nach 180°. tan(alpha+180)=tan(alpha), allgemeiner: tan(alpha+n*180)=tan(alpha), n=1, 2, 3, ... Wandert der Punkt P von der x-Achse aus im Uhrzeigersinn, so werden die Winkel negativ. Dann gilt tan(alpha-n*180)=tan(alpha), n=1, 2, 3, ... Ein Graph stellt diesen Sachverhalt noch einmal dar. 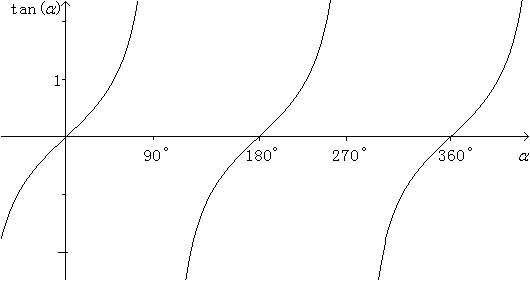 Es ist üblich und auch sinnvoll, die Winkel der Tangensfunktion nicht im Gradmaß, sondern im Bogenmaß anzugeben. Dann schreibt man f(x)=tan(x) oder y=tan(x) an Stelle von f(alpha)=tan(alpha). Der Definitionsbereich ist D=|R \ {[(2k-1)/2]pi, k=...-2 ,-1 ,0 , 1, 2,...}. 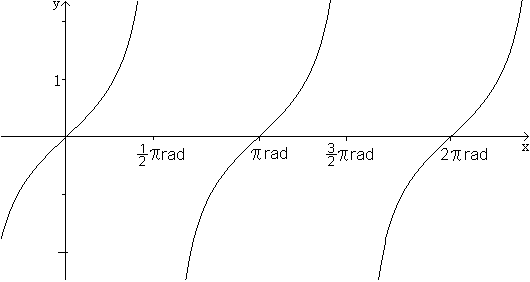
Kotangensfunktion für D=|R. 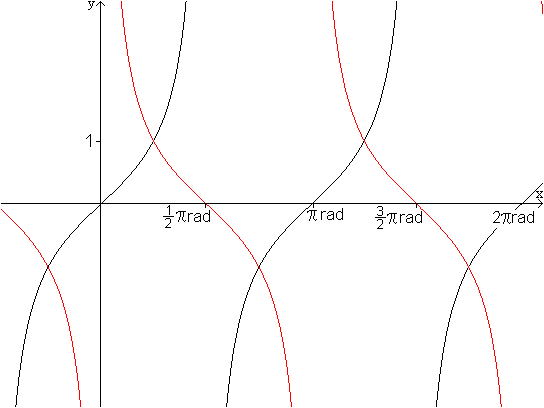 Wie oben erwähnt, gilt für die Kotangensfunktion
cot(alpha)=tan(90°-alpha).
Ermittlung
der Tangenswerte top
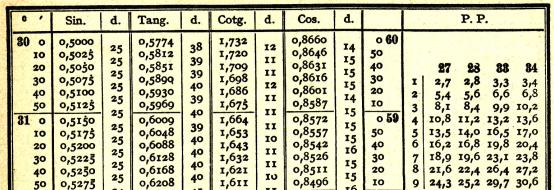
Funktionswerte mit dem Tafelwerk In Vor-Taschenrechner-Zeiten standen die Funktionswerte in einem Tafelwerk ("Logarithmentafeln") bereit.
Die Tabellen enthalten Tangenswerte für Winkel auf
1'=1/60° genau.
Berechnung der Tangenswerte Die Tangenswerte kann man für Winkel |x|<pi/2 nach der Taylor-Reihe, entwickelt um x=0, berechnen.
Die Formel wird lesbarer, wenn man sich auf die ersten Glieder beschränkt. Der Taschenrechner liefert tan(30,0°)=tan(pi/6 rad)=0,5774. Die Reihe liefert tan(pi/6 rad)=0,52360+0,04785+0,00525+0,00058=0,5773. Formeln top
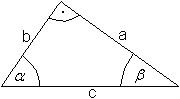
Beziehung zum Sinus und Kosinus Es gilt tan(alpha)=sin(alpha)/cos(alpha). Herleitung für spitze Winkel: tan(alpha)=y/x=(y/r)/(x/r)=sin(alpha)/cos(alpha). Additionstheorem Es gilt tan(alpha+beta)=[tan(alpha)+tan(beta)]/[1-tan(alpha)tan(beta)] Herleitung tan(alpha+beta) = sin(alpha+beta)/cos(alpha+beta) = [sin(alpha)cos(beta)+cos(alpha)sin(beta)]/[cos(alpha)cos(beta)-sin(alpha)sin(beta)] = [sin(alpha)/cos(alpha)+sin(beta)/cos(beta)]/[1-sin(alpha)/cos(alpha)sin(beta)cos(beta)] = [tan(alpha)+tan(beta)]/[1-tan(alpha)tan(beta)] Tan(n*alpha) Ist alpha=beta, so lautet die Formel tan(2alpha)=2tan(alpha)/[1-tan²(alpha)]. Die Verallgemeinerung ist tan(n*alpha)={tan[(n-1)alpha]+tan(alpha)}/{[1+tan[(n-1)alpha)]tan(alpha)}. Beweis durch vollständige Induktion Induktionsanfang (n=2) tan(2alpha)=[tan(alpha)+tan(alpha)]/[1+tan(alpha)tan(alpha)]=2tan(alpha)/[1-tan²(alpha)] Induktionsvoraussetzung (richtig für n) tan(n*alpha)={tan[(n-1)alpha]+tan(alpha)}/{[1+tan[(n-1)alpha]tan(alpha)} Induktionsschluss (Beweis für n+1) tan[(n+1)alpha]=tan(n*alpha+alpha)=[tan(n*alpha)+tan(alpha)]/[1-tan(n*alpha)tan(alpha)], wzbw. Die Formeln zum Tangenssatz stehen auf meiner Webseite Allgemeines Dreieck. Weitere Formeln zum Tangens findet man auf der Webseite Tangent von MathWorld (URL unten). Eigenschaften
der Tangensfunktion top
 Definitions- und Wertebereich
Periode Es gilt tan(alpha+180°)=tan(alpha) oder tan(x+pi)=tan(x). Damit ist die Tangensfunktion eine periodische Funktion mit der (kleinsten) Periode 180° oder pi rad. Besondere Punkte
Symmetrie Die Tangensfunktion ist punktsymmetrisch bezüglich des Nullpunktes. Es gilt tan(x)= - tan(-x). Ableitung Es gilt f '(x)=1/cos²(x). Herleitung Nach der Quotientenregel gilt [tan(x)]'=[sin(x)/cos(x)]'=[cos²(x)+sin²(x)]/cos²(x)=1/cos²(x), wzbw.. Unten im Kapitel Arkusfunktion wird die Gleichung cos²(x)=1/[1+tan²(x)] hergeleitet, so dass auch gilt f '(x)=1+tan²(x). Integral ... 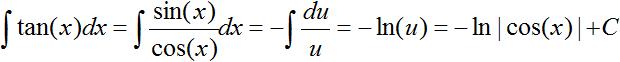
Substitution: cos(x)=u und dx=-du/sin(x). Bekannte Aufgaben top
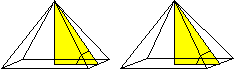
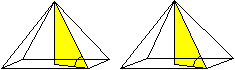
Die Variable m ist die Steigung der Geraden. Es gilt m=tan(alpha). In der Zeichnung ist die Normalform y=(1/2)x+1 und der Steigungswinkel alpha=26,6°. Winkel in der Quadrat-Pyramide Bei einer Pyramide gibt es zwei bemerkenswerte Winkel, nämlich der Winkel alpha1 zwischen der Grundfläche und einer Seitenfläche und der Winkel alpha2 zwischen der Grundfläche und einer Seitenkante. Sie lassen sich aus der Grundseite a und der Höhe h mit Hilfe der Tangensfunktion berechnen. Die Winkel sind eindeutig, wenn die Grund- und die Seitenkante gleich groß sind. Dieser Fall soll betrachtet werden. Die Pyramide heißt für diesen Sonderfall Quadratpyramide. Für sie gilt h=(1/2)sqrt(2)a. Alpha1
Alpha2
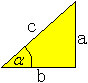
Steigung einer Straße Es gibt Straßenabschnitte, die so steil sind, dass es geboten erscheint, sie den Verkehrsteilnehmern vorher anzuzeigen. Es gibt dazu Verkehrsschilder, auf denen eine Prozentzahl als Maß für die Steigung steht, z.B. 10%.
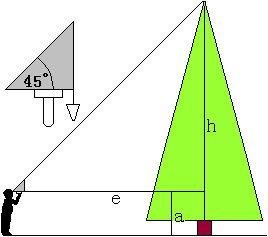
Anmerkung Die größte Steigung hier im Kreis Lippe hat die Gauseköte im Teutoburger Wald mit bis zu 16% Steigung. Höhe eines Baumes
Arkustangens top
Arkustangenswerte mit dem Taschenrechner Gibt man in den Taschenrechner einen Tangenswert ein, so wird nach Maßgabe der Umkehrfunktion ein Winkel zwischen -(1/2)pi und +(1/2)pi bzw. -90° und +90° ausgegeben. So erhält man zum Tangenswert 0,5774 den Winkel 30,0° über die Tastenfolge (2nd) (tan)... Man schreibt arc tan(0,5774)=30,0°. Zwei weitere Beispiele sind arc tan(0,3333)= 18,4° und arc tan(-0,3333)= -18,4°. Ableitung Behauptung: Die Ableitung der Funktion g(x)=arc tan(x) ist g'(x)=1/(1+x²). Herleitung Vorweg wird die Gleichung cos²(x)=1/[1+tan²(x)] bestimmt. Aus tan²(x)=sin²(x)/cos²(x) folgt cos²(x)tan²(x)=1-cos²(x) oder cos²(x)=1/[1+tan²(x)]. Unten braucht man cos²(y)=1/[1+tan²(y)]. Da g mit g(x)=arc tan(x) die Umkehrfunktion von f mit f(x)=tan(x) ist, folgt aus y=arc tan(x) die Gleichung x=tan(y). Dann gilt für die Ableitungen g'(x)=1/f'(y). Dann ist [arc tan(x)]'=1/tan'(y)=1/[1/cos²(y)]=cos²(y)=1/[1+tan²(y)]=1/(1+x²). Unbestimmtes Integral
Daraus folgt 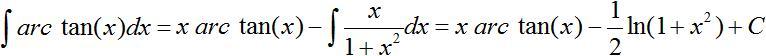
Dabei wird verwendet, dass H(x)=(1/2)ln(1+x²) die Stammfunktion von h(x)=x/(1+x²), wie man durch Ableiten von H(x) zeigen kann. Reihe Wie zur Tangensfunktion gibt es auch zur Arkustangensfunktion eine konvergente Reihe. Sie lautet arc tan(x) = x - (1/3)x3 + (1/5)x5 - (1/7)x7+(1/9)x9 - +... Immer wieder erstaunlich ist die Reihe für den Sonderfall x=1. Die Reihe ist arc tan(1) = 1 - 1/3+ 1/5- 1/7 + 1/9 - ...+... Da arc tan(1)=pi/4 gilt, ergibt sich eine Formel zur Berechnung von pi. Die ersten sechs Summanden führen zu pi=3,35. Es gibt bessere Annäherungen an pi. Tangenskurven top
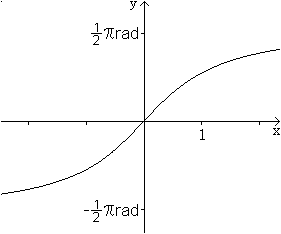
Stammfunktion und Ableitung von g(x)=arc tan(x)
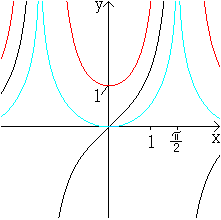
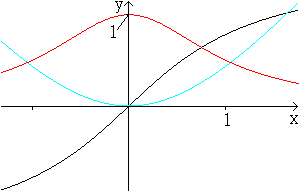
Vier Kurven im Vergleich
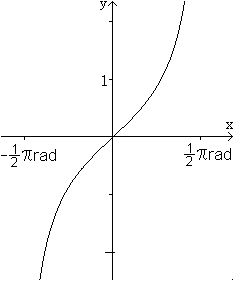
Spiegelbilder zum Tangens
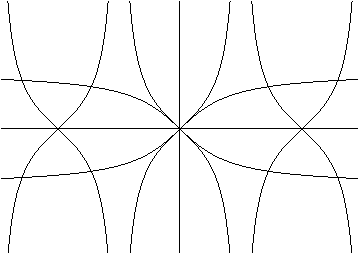
Der Tangens im Polarkoodinatensystem
Übersicht
über die trigonometrischen Funktionen top
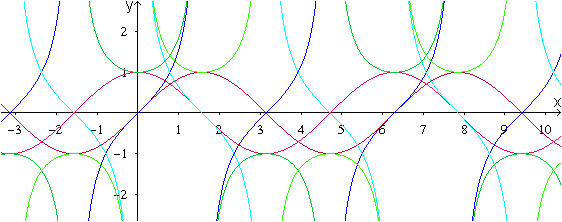
Alle Graphen in einem Bild
In der Schule finden heute nur der Sinus, der Kosinus und der Tangens Verwendung. Der Kotangens ist aus den Schullehrbüchern weitgehend verschwunden. Ich entdeckte den Sekans und den Kosekans zuerst in englischen Schulbüchern. Tangensfunktion im Internet top Deutsch André Mössner
Matroid
Werner Brefeld
Wikipedia
Englisch School of Mathematics and Statistics - University of St
Andrews, Scotland
Eric W. Weisstein (MathWorld)
Richard Parris (Freeware-Programme)
Wikipedia
Wolfram Matematica
Referenzen
top
URL meiner Homepage: https://www.mathematische-basteleien.de/ © 2011 Jürgen Köller |
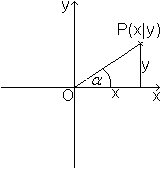 ...
...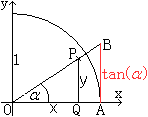 ...
...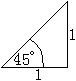 ...
...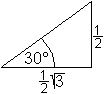 ...
...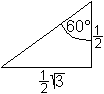 ...
...
 ...
... ...
...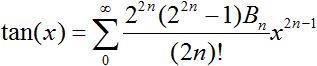
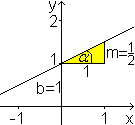 ...
... ...
... ...
... ...
...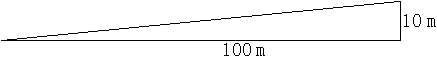 ...
... ...
... ...
... ...
... ...
... ...
...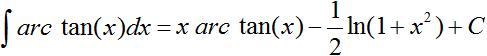
 ...
... ...
...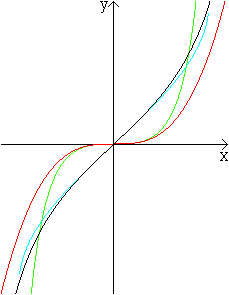 ...
... ...
...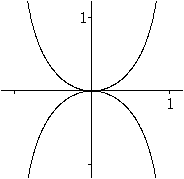 ...
...