|
Was ist die quadratische Pyramide?
... ... ... |
Gegeben sind ein ebenes Vieleck und ein Punkt, der nicht
in der Ebene des Vielecks liegt.
Verbindet man diesen Punkt mit den Ecken des Vielecks,
so entsteht die (allgemeine) Pyramide. |
... ... ... |
Pyramiden unterscheidet man nach der Form der Grundfläche.
Es gibt Dreieck-, Viereck-, Fünfeckpyramiden ...
... ... ... |
Ist die Grundfläche der Pyramide ein Quadrat und
liegt die Spitze über der Mitte des Quadrates, so entsteht die gerade,
quadratische Pyramide, auf dieser Seite einfach Pyramide genannt. |
... ... ... |
Beschreibung
der Pyramide
top
Flächen
... ... ...
|
... ... ... |
Die Pyramide besteht aus einem Quadrat als Grundfläche
und aus vier gleichschenkligen Dreiecken als Seitenflächen.
Neben den fünf Flächen hat sie fünf Eckpunkte
und acht Kanten. |
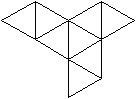
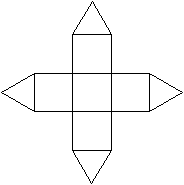
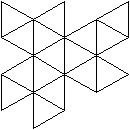
Alle
Netze

Vier
Symmetrie-Ebenen
... |
Die Pyramide ist vierfach drehsymmetrisch bzgl. der Höhe. |
Besondere
Ansichten

Blick von oben
|
Blick auf eine Seitenfläche
|
Blick auf die Grundkante
|
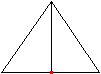
Blick auf die Ecke vorne
|
In allen Fällen handelt
es sich um Parallelprojektionen der Pyramide.
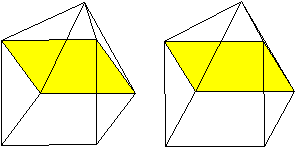
Dualität
...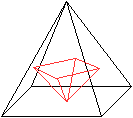 ... ... |
Verbindet man die Mittelpunkte der Flächen einer
Pyramide miteinander, entsteht wieder eine Pyramide.
Das liegt daran, dass die Pyramide sowohl fünf Flächen
als auch fünf Eckpunkte hat. |
Größen
der Pyramide
top
Die Pyramide wird im Allgemeinen
durch die Grundkante (Quadratseite)
a und die Raumhöhe h
bestimmt.
Daraus lassen sich weitere Größen wie die
Seitenkante s, die Dreieckshöhe
h1,
der Mantel M, die Oberfläche O, das Volumen V
und die Winkel zwischen den Flächen epsilon1'2'3
berechnen.
Längen
...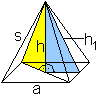 ... ... |
Es gilt s²=h²+[(1/2)sqrt(2)a]²=h²+a²/2.
Dann ist s=sqrt[h²+(1/2)a²] oder s=(1/2)sqrt(2a²+4h²).
Es gilt h1²=h²+(a/2)².
Dann ist h1=(1/2)sqrt(a²+4h²). |
Flächen
... ... ...
|
 ... ...
|
Die vier Seitenflächen bilden den Mantel. Es gilt
M=2ah1 oder M=a*sqrt(4h²+a²).
Die Oberfläche O setzt sich zusammen aus der Grundfläche
und dem Mantel.
Es gilt O=a²+2ah1
oder
O=a²+a*sqrt(4h²+a²). |
Volumen
Das Volumen einer Pyramide ist V=(1/3)a²h.
Erste Herleitung
Man legt dazu um die Pyramide einen
Treppenkörper aus n quadratische Scheiben, bestimmt das Volumen der
n Scheiben und lässt in der Formel die Anzahl n der Scheiben über
alle Grenzen gehen. Aus dem Treppenkörper wird die Pyramide.
...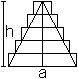 ... ... |
Das Volumen von 5 Scheiben ist
V5=(1/5)a²h+(1/5)(a-a/5)²h+(1/5)(a-2a/5)²h+(1/5)(a-3a/5)²h+(1/5)(a-4a/5)²h
und
V5=(1/5³)(5²+4²+3²+2²+1²)a²h |
Das Volumen für n Scheiben ist
Vn=(1/n³)(1²+2²+3²+
...+n²)a²h.
Es gilt die Formel 1²+2²+3²+
...+n²=(1/6)n(n+1)(2n+1).
Dann ist Vn=(1/n³)[(1/6)n(n+1)(2n+1)]a²h=(1/6)(1+1/n)(2+1/n)a²h
Lässt man n gegen Unendlich
gehen, dann wird Vn zu V=(1/3)a²h.
Das ist die gesuchte Formel.
Zweite Herleitung
...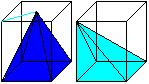 ... ...
|
...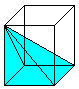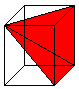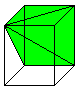 ... ...
|
Legt man um die Pyramide ein quadratisches Prisma mit
dem Volumen V=a²h und verschiebt die Spitze der Pyramide in eine Prismenecke,
so entsteht eine schiefe Pyramide mit gleichem Volumen. Dann gibt
es noch zwei weitere Pyramiden gleichen Volumens. Die drei Pyramiden füllen
das Prisma aus. |
Das Volumen einer Pyramide ist dann V=(1/3)*a²h.
Winkel
Bei der Pyramide sind drei Winkel
von Interesse. Das sind der Winkel zwischen einer Seitenfläche und
der Grundfläche (epsilon1), der Winkel zwischen zwei nebeneinander
liegenden Seitenflächen ( epsilon2) und der Winkel, den
zwei gegenüberliegende Flächen einschließen (epsilon3).
Epsilon1
..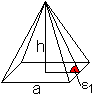 .... .... |
Der Neigungswinkel (Böschungswinkel) einer Seitenfläche
gegenüber der Grundfläche kennzeichnet gut die Form einer Pyramide.
Es gilt tan(epsilon1)=h/(a/2)
oder tan(epsilon1)=2h/a. |
Epsilon2
...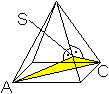 ...
... |
Der Winkel zwischen zwei nebeneinander liegenden Seitenflächen
taucht in einem Dreieck auf. Man zeichnet dazu durch gegenüberliegende
Eckpunkte A und C des Grundquadrates zu der gemeinsamen Kante die Senkrechten
(Höhen). Sie treffen sich im Punkt S auf der Kante. |
Im so entstandenen Dreieck ACS ist der Innenwinkel bei Punkt
S der gesuchte Schnittwinkel epsilon2.
Für den Winkel epsilon2
gilt cos(epsilon2)=-a²/(a²+4h²).
Herleitung
Das Dreieck ACS wird aus der Pyramide gelöst.
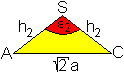
Nach dem Kosinussatz gilt 2a²=2h2²-2h2²cos(epsilon2)
oder cos(epsilon2)=(h2²-a²)/h2².
Mit den Formeln ADreieck=(1/2)ah1
und ADreieck=(1/2)sh2 ergibt sich ah1=sh2
oder h2 =(a/s)h1.
Das führt zu cos(epsilon2)=(h1²-s²)/h1².
Aus s²=(1/4)a²+h1²
folgt h1²-s²=-(1/4)a². Außerdem ist h1²=(1/4)a²+h².
Dann ist cos(epsilon2)=(h1²-s²)/h1²=[-(1/4)a²]/[(1/4)a²+h²]=-a²/(a²+4h²).
Epsilon3
...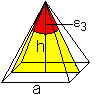 ... ... |
Der Winkel zwischen zwei nebeneinander liegenden Seitenflächen
taucht in einem Dreieck auf.
Man zeichnet dazu durch die Spitze der Pyramide zwei
Seitenhöhen ein. |
Es gilt tan(epsilon3/2)=(a/2)/h
oder tan(epsilon3/2)=a/(2h).
Schwerpunkt
...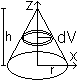 ... ... |
Der Schwerpunkt der Pyramide liegt auf der Höhe
h im Abstand zs=(1/4)h über der Grundebene. |
Eine Rechnung findet man auf meiner Seite Kegel.
Man muss dort nur an Stelle der Kreisflächen Quadratflächen
betrachten.
Die
Pyramide in der analytischen Geometrie top
Eine neue Sicht auf die Pyramide erhält man, wenn
man die Ebenen betrachtet, in denen die Seitenflächen und die Grundfläche
liegen.
...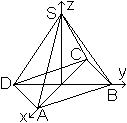 ... ... |
Man führt ein räumliches, kartesisches Koordinatensystem
in folgender Weise ein.
Der Nullpunkt ist der Mittelpunkt des Grundquadrates.
Die Diagonalen liegen auf der x- bzw. y-Achse.
Die Höhe liegt auf der z-Achse. |
Das Besondere ist, dass die
vier Seitenflächen Ebenen bilden, die sich in einem Punkt, der Spitze
der Pyramide, schneiden. Ihre Spurgeraden bilden die Grund- und Seitenkanten.
Die Gleichungen der Seitenebenen
und ihrer Spurgeraden erhält man über die Achsenabschnittsform.
Es ist e=(1/2)sqrt(2)a zur Abkürzung.
Seitenflächen
EABS: x/e+y/e+z/h=1
EBCS: -x/e+y/e+z/h=1
EDCS: -x/e-y/e+z/h=1
EDAS: x/e-y/e+z/h=1 |
Grundkanten
gAB: x/e+y/e=1
gBC: -x/e+y/e=1
gCD: -x/e-y/e=1
gDA: x/e-y/e=1 |
Seitenkanten
gAS: x/e+z/h=1
gBS: y/e+z/h=1
gCS: -x/e+z/h=1
gDS: -y/e+z/h=1 |
Das Grundquadrat liegt in der Ebene z=0.
Pyramide in einer
Kugel top
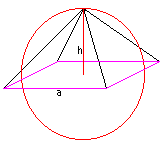
1) Pyramide gegeben
In eine Kugel passt eine Pyramide,
deren Eckpunkte auf der Kugeloberfläche liegen. Sie heißt die
Umkugel der Pyramide.
...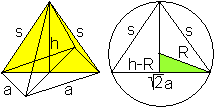 ... ... |
Der Radius R der Umkugel ist aus Symmetriegründen
der Radius des Umkreises des Dreiecks, das aus zwei Kanten und der Diagonalen
des Quadrates gebildet wird.
Der Radius ist R=(a²+2h²)/(4h). |
Herleitung
Nach dem Satz des Pythagoras gilt
R²=[1/2)sqrt(2)]²+(h-R)² oder R²=(1/2)a²+h²-2hR+R²
oder (1/2)a²+h²=2hR.
Daraus folgt R=(a²+2h²)/(4h).
2) Kugel gegeben
Ist die Kugel mit dem Radius R vorgegeben, so stellt
sich die Frage nach der Pyramide mit dem größten Volumen.
Für diese Fragestellung habe die Pyramide die Höhe
y und die Grundkante x.
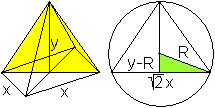 |
Die Zielfunktion ist V=(1/3)x²y.
Die Nebenbedingung steht schon oben. Aus (1/2)a²+h²=2hR
wird hier (1/2)x²+y²=2yR.
Daraus ergibt sich x²=4Ry-2y².
Dann ist V(y)=(1/3)(4Ry-2y²)y=(4/3)Ry²-(2/3)y³.
Die Bedingung V'(y)=0 führt
zu (8/3)Ry-2y²=0 oder y=(4/3)R. Weiter ist x=(4/3)R |
Ergebnis: Eine Pyramide, bei der die Längen der Höhe
und der Grundkante gleich sind, hat das größte Volumen.
Es ist x=y=(4/3)R.
Körper in
der Pyramide top
Inkugel
...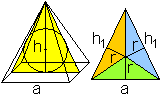 ... ... |
Der Radius der Inkugel ist aus Symmetriegründen
der Radius des Inkreises des Dreiecks, das aus zwei Seitenhöhen und
der Mittelparallele des Quadrates gebildet wird.
Der Radius ist r=[a*sqrt(a²+4h²)-a²]/(4h). |
Herleitung
Der Flächeninhalt des Dreiecks
lässt sich direkt oder als Summe der Flächeninhalte dreier Teildreiecke
bestimmen.
Es gilt (1/2)ah=(1/2)ar+2*(1/2)h1r
oder ah=ar+2h1r oder r=ah/(a+2h1).
Ersetzt man h1 durch
h1=(1/2)sqrt(a²+4h²),
so ist r=ah/[a+sqrt(a²+4h²)]={ah[a-sqrt(a²+4h²)]}/(-4h²)=[a*sqrt(a²+4h²)-a²]/(4h).
Halbkugel
in der Pyramide
...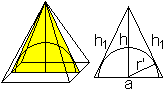 ... ... |
Der Radius r' der Halbkugel ist aus Symmetriegründen
der Radius des Halbkreises des Dreiecks, das aus zwei Seitenhöhen
und der Mittelparallelen des Quadrates gebildet wird.
Der Radius ist r'=[ah*sqrt(a²+4h²)]/(a²+4h²). |
Herleitung
Für den Flächeninhalt
des Dreiecks gilt (1/2)ah=2*[(1/2)h1r'] oder r'=(1/2)ah/h1
oder r'=[ah*sqrt(a²+4h²)]/(a²+4h²).
Würfel
in der Pyramide
...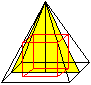 ... ... |
In die Pyramide passt ein Würfel. Seine Kantenlänge
ist x=ah/(a+h). |
Herleitung
...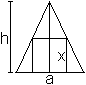 ... ... |
Man kann im Dreieck, das aus zwei Seitenhöhen und
der Mittelparallelen des Quadrates gebildet wird, nach dem 2.Strahlensatz
die Proportion a:x=h:(h-x) ablesen. Daraus folgt die Produktgleichung a(h-x)=hx
oder ah-ax=hx oder x=ah/(a+h). |
Größte
Pyramide in der Pyramide
...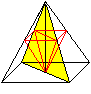 ... ... |
Eine Pyramide mit der Grundseite x und der Höhe
y liegt kopfüber in einer festen Pyramide. |
Je kleiner die Höhe y wird, desto kleiner wird auch
sein Volumen. Je mehr sich die Höhe y der Höhe h nähert,
desto kleiner wird das Volumen. Dazwischen liegt eine Pyramide, deren Volumen
maximal ist.
Lösung: Das Volumen ist maximal,
wenn die Höhe
y=(1/3)h und die Grundseite x=(2/3)a ist.
Herleitung
Die Zielfunktion ist V=(1/3)x²y.
...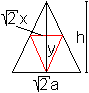 ... ... |
Zur Angabe einer Nebenbedingung
betrachtet man das Dreieck aus zwei Seitenkanten und einer Diagonalen
im Grundquadrat.
Es gilt nach dem 2.Strahlensatz
die Proportion h:(h-y)=(a/2):(x/2). Die Produktgleichung ist hx/2=a(h-y)/2
oder ax=ah-ay oder y=(ah-hx)/a. |
Dann ist V=(1/3)x²y oder V=(1/3)x²(ah-hx)/a oder
V(x)=(1/3)hx²-(1/3)(h/a)x³.
Mit V'(x)=0 erhält man neben x=0 auch x=(2/3)a und
weiter y=(1/3)h, wzbw..
Größtes
Prisma in der Pyramide
...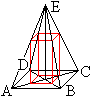 ... ... |
In eine Pyramide passt ein quadratisches Prisma. Das
Prisma mit dem größten Volumen hat die Grundseite (2/3)a und
die Höhe h/3.
Die Lösung und auch die Rechnung entsprechen der
Rechnung zur größten Innenpyramide im letzten Kapitel. |
Besondere Pyramiden
top
J1 Quadratpyramide
Die quadratische Pyramide mit gleichen Kanten und somit
eine Pyramide mit regelmäßigen Figuren als Begrenzungsflächen
gehört zu den Johnson-Körpern.
Sie heißt Quadratpyramide und ist der Johnson-Körper Nr. 1,
kurz J01.
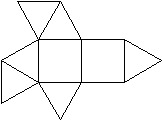
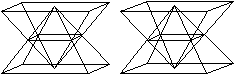
Seitenansicht
|
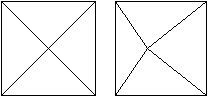
Aufsicht
|
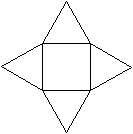
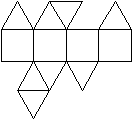
Netz
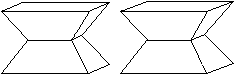
|
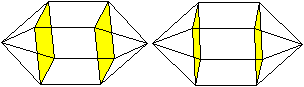
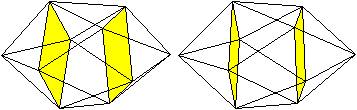
Die Bildpaare ermöglichen eine dreidimensionale Sicht
des Körpers.
Größen
der Quadratpyramide
Da s=a gilt, vereinfachen sich die Formeln der allgemeinen
Pyramide von oben.
Es gilt
h²=s²-[(1/2)sqrt(2)a]² = a²-a²/2
= (1/2)a² oder h = (1/2)sqrt(2)a = 0,71a.
h1 = (1/2)sqrt(3)a = 0,87a
V= (1/3)a²h = (1/3)a²(1/2)sqrt(2)a = (1/6)sqrt(2)a³
= 0,24a³
O= a²+a*sqrt(a²+4h²) = a²+a*sqrt(a²+2a²)
= [1+sqrt(3)]a² = 2,73a²
R= (a²+2h²)/(4h) = 2a²/[2sqrt(2)]a = a/sqrt(2)
= (1/2)sqrt(2)a = 0,71a
r= [a*sqrt(a²+4h²)-a²]/(4h) = [sqrt(3)-1]a/[2sqrt(2)]
= (1/4)[sqrt(6)-sqrt(2)]a = 0,26a
r'= [ah*sqrt(a²+4h²)]/(a²+4h²) = [a*sqrt(2)sqrt(3)]/3
= (1/6)sqrt(6)a = 0,41a
Die Zahlen am Ende der Zeilen dienen der Veranschaulichung
und sind auf Hunderstel gerundet.
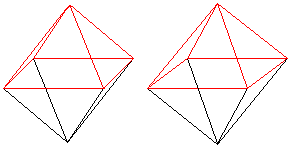
Oktaeder
Spiegelt man die Quadratpyramide an der Grundfläche,
erhält man das Oktaeder, einen der fünf
platonischen
Körper.
J8
Verlängerte Quadratpyramide
Setzt man auf einen Würfel
eine Quadratpyramide, so erhält man einen Körper, der
von vier gleichseitigen Dreiecken und fünf Quadraten begrenzt wird.
Er ist der Johnson-Körper J08, die verlängerte Quadratpyramide.
J15 Verlängerte tetragonale
Bipyramide
Setzt man auf die gegenüberliegenden Quadrate eines
Würfels zwei Pyramiden, entsteht der Johnson-Körper J15, die
verländerte
tetragonale Bipyramide.
J17 Verdreht verlängerte Quadratbipyramide
(J17)
Setzt man auf die gegenüberliegenden
Quadrate eines quadratischen
Antiprismas zwei Pyramiden, entsteht der Johnson-Körper J17, die
verdreht
verlängerte Quadratbipyramide.
J49 Erweitertes dreieckiges Prisma
Setzt man auf ein gleichkantiges
Prisma
eine Pyramide, so entsteht der Johnson-Körper J49, das erweiterte
dreieckige Prisma.
Pyramiden im Würfel
...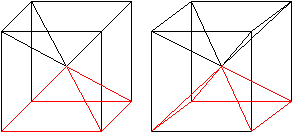 ... ... |
Zeichnet man in einen Würfel der Kantenlänge
a die vier Raumdiagonalen ein, so wird er in sechs gleich große Pyramiden
aufgeteilt.
Die Höhe einer Pyramide ist h=a/2, das Volumen ist
V=a³/6.
Der Neigungswinkel beträgt epsilon1=45°. |
Rhombendodekaeder
...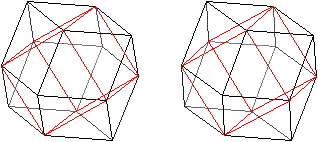 ... ... |
Setzt man auf die sechs Seitenflächen eines Würfels
die Pyramiden der letzten Zeichnung, so entsteht ein Rhombendodekaeder.
Bei ihm haben die aufgesetzten Pyramiden die Höhe
(1/2)a. |
Haben die aufgesetzten Pyramiden
eine kleinere Höhe als (1/2)a, so entsteht ein Tetrakishexaeder (s.u.
bei Wikipedia).
Ist die Höhe größer als (1/2)a, so entsteht
ein dreidimensionaler Stern.
...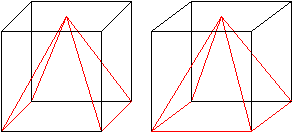 ... ... |
Verbindet man die Flächenmitte eines Quadrates mit
den Eckpunkten des gegenüberliegenden Quadrates, so entsteht eine
Pyramide mit der Eigenschaft h=a.
Das Volumen ist V=(1/3)a³.
Der Neigungswinkel beträgt arc tan(2)=63,4°. |
Pyramidenstumpf
...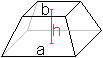 ... ... |
Legt man durch eine Pyramide eine Schnittebene parallel
zur Grundebene, entsteht eine kleinere Pyramide und ein Pyramidenstumpf. |
Zwei Pyramidenstümpfe
können entstehen, wenn sich Pyramiden durchdringen.
Berechnungen top
Eine Pyramide wird wie oben gezeigt
im Allgemeinen durch die Quadratseite
a und die Raumhöhe h
bestimmt. Andere Größen wie die Seitenkante s, der Mantel
M
oder das Volumen V kann man dann aus diesen berechnen. Dazu stehen
folgende Formeln zur Verfügung.
s²=h² + a²/2
M²=a^4
+ 4a²h²
V=(1/3)a²h
Man kann verallgemeinern: Sind von
den fünf Größen a, h, s, M und V zwei gegeben, so lassen
sich die übrigen drei berechnen.
Es gibt 10 Fälle.
1) Gegeben: a,h. Gesucht: V,s,M.
Lösung: V=1/3a²h, s=1/2*sqr(2a²+4h²),
M=a*sqr(a²+4h²).
2) Gegeben: a,s. Gesucht: h,V,M.
Lösung: h=1/2*sqr(4s²-2a²),
V=1/6*a²*sqr(4s²-2a²), M=a*sqr(4s²-a²).
3) Gegeben: h,s. Gesucht:
a,V,M.
Lösung: a=sqr(2s²-2h²),
V=2/3*h*(s²-h²), M=2*sqr(s^4-h^4).
4) Gegeben: a,V. Gesucht: h,s,M.
Lösung: h=3V/a², s=1/2*1/a²*sqr(2a^6+36V²),
M=1/a*sqr(a^6+36V²).
5) Gegeben: h,V. Gesucht: a,s,M.
Lösung: a=1/h*sqr(3hV), s=1/2*1/h*sqr(4h^4+6hV),
M=1/h*sqr(9V²+12h³V).
6) Gegeben: s,V.
Gesucht: h,a,M
Lösung: h³-s²h+3/2*V=0
und a^6-2s²a^4+18V²=0 sind zu lösen :-(, dann ist
M=a*sqr(a²+4h²).
7) Gegeben: a,M.
Gesucht: s,h,V.
Lösung: s=1/2*1/a*sqr(M²+a^4),
h=1/2*1/a*sqr(M²-a^4), V=1/6*a*sqr(M²-a^4).
8) Gegeben: h,M.
Gesucht: s,a,V.
Lösung: s=1/2*sqr[sqr(4M²-16h^4)],
a=sqr[sqr(M²-4h^4)-2h²)],
V=1/3*h*[sqr(M²-4h^4)-2h²].
9) Gegeben: s,M.
Gesucht: h,a,V.
Lösung: h=1/2*sqr[sqr(16s^4-4M²)],
a=sqr[2s²-sqr(4s^4-M²)],
dann V=1/3*a²h.
10) Gegeben: M,V.
Gesucht: a,h,s.
Lösung: a^6-M²a²+36V²=0
und 12Vh³-M²h²+9V²=0 sind zu lösen :-(, dann ist
s=1/2*sqr(2a²+4h²).
(Dank an 10b in 1992/93)
Man kann die zehn Aufgabentypen
in der Schule gut für einen "arbeitsteiligen Gruppenunterricht" verwenden.
Man teilt die Klasse in zehn Gruppen auf und ordnet ihnen je nach Leistungsvermögen
einen Typ zu. Ziel ist es, in einer Woche eine Lösung zu finden und
aufzuschreiben.
Andere geeignete und erprobte Themen auf meiner Homepage
sind Kreisteile,
Geometrische
Folgen und Reihen und harmonischen Schwingungen
(in der Physik).
Pyramidenzahlen top
...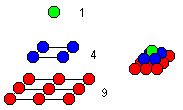 ... ... |
Man kann Kugeln zu einer Pyramide aufschichten. Die Anzahl
der Kugeln in einer Schicht ist eine Quadratzahl: 1,4,9,16,... , allgemein
n². Bildet man die Summe der Kugeln schichtweise, so erhält man
die "Pyramidenzahlen" 1,5,14,30,... , allgemein 1+4+9+16+...+n²=n(n+1)(2n+1)/6. |
Früher bewahrte man so Kanonenkugeln auf und konnte
mit Hilfe der Anzahl der Schichten auf die Anzahl der Kanonenkugeln schließen.
Es sieht auch schön
aus, Kugeln zu Pyramiden zu stapeln. Dann müssen die Kugeln der untersten
Schicht in Mulden oder in einem Rahmen liegen.
Die Cheopspyramide
von Gizeh top
Wenn man von einer Pyramide spricht,
meint man meist die Große Pyramide, das Grabmal des Pharaos Cheops
aus der 4.Dynastie (2500 v.Chr.), gelegen etwa 15km südlich des Zentrums
von Kairo in Sichtweite des Nils in Ägypten.
Die Cheopspyramide ist ein Bauwerk
der Superlative:
> Sie ist das einzige der sieben
Weltwunder, das zum überwiegenden Teil erhalten ist.
> Sie war bis zur Neuzeit das größte
Bauwerk.
> Sie zählt zu den bekanntesten
Bauwerken der Welt.
Die Maßzahlen der Höhe und der
Seitenlänge des Grundquadrates der Cheopspyramide unterscheiden sich
in der Literatur. Ich verwende die Daten aus einem neuen Reiseführer
(5) in der Hoffnung, dass hier die letzten Forschungen berücksichtigt
sind.
...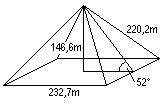 ... ... |
Die Pyramide ist heute 137,0m hoch
und 230,5m lang. Ursprünglich war sie etwas größer (links).
Sie umfasst eine Fläche von etwa 5 ha. Etwa 2,5 Millionen Blöcke
mit je fast 1m³ Volumen bilden die Pyramide. Die Verkleidung aus geschliffenen
Kalkplatten ist nicht erhalten geblieben. |
Gibt man die ursprünglichen Daten a=232,7m
und h=146,6m vor, so sind die Seitenkanten s=220,4m, das Grundquadrat 5,4150
ha, der Mantel 8,7120 ha, die Oberfläche 14,13 ha, das Volumen 2646000
m³ und der Neigungswinkel 51,6° groß.
Das Volumen sei veranschaulicht: Stellt
man sich vor, ein Steinblock sei ein Würfel mit der Kantenlänge
1m, so würden sie aneinandergereiht eine Schlange der Länge von
etwa 2500 km bilden. Das ist etwa die Entfernung London - Athen.
(Unglaulich, habe ich da eigentlich richtig gerechnet?)
Zahlenmystik
zur Cheopspyramide
top
Aussagen, Erläuterungen.
1
... ... ... |
Flächeninhalt des Quadrates über der Höhe:
h² = 21780m².
Flächeninhalt einer Seitenfläche: (1/2)*a*h'
= 21490m².
Vermutung: Die Flächen sind gleich groß. (nach
Herodot). |
Aus der Gleichheit der Flächen
h²=(1/2)*a*h' und aus dem Satz des Pythagoras (h²+a²/4=h'²)
folgt das Verhältnis a:h= sqr(sqr(20)-2)=1,5723... . Das ist etwa
3,1446../2 oder Pi/2.
Es folgt auch aus der Gleichheit der Flächen
h²=(1/2)*a*h' und aus dem Satz des Pythagoras (h²+a²/4=h'²)
das zweite Verhältnis h':(a/2)=1/2*[1+sqr(5)]. Das ist das Goldene
Verhältnis phi = =1,6180... .
2
...... |
Umfang der quadratischen Grundfläche: 4a=930,8m
Umfang des Kreises mit dem Radius h: 2*pi*h=921,1m
Vermutung: Die Umfänge sind gleich...................... |
... ... ... |
Die alten Ägypter kannten
das Verhältnis [Kreisumfang : Kreisdurchmesser] als 256/81 (Rhind
Papyrus 1850 v.Chr.). Es führt zu pi=3,16... (Buch 4).
Der Kreis spielt als Sonnenscheibe
eine zentrale Rolle in der altägyptischen Mythologie und schmückt
zum Beispiel das Haupt der Göttin Hathor (links).
In dem TV-Film von Hoimar von
Ditfurth (5) wird die Gleichheit der Umfänge dadurch erklärt,
dass längs einer Quadratseite ein Kreis abgerollt wurde und Kreise
gleichen Durchmessers auf Raumhöhe gestapelt wurden. Auf diese Weise
taucht das Verhältnis [Umfang : Durchmesser]=pi auf. |
3
...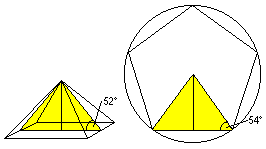 ... ... |
Legt man durch die Mitte der Pyramide parallel zu einer
Quadratseite einen Vertikalschnitt, so entsteht ein Dreieck. Dieses Dreieck
kommt dem Bestimmungsdreieck eines regelmäßigen Fünfecks
nahe. In einem Fünfeck ist das Besondere, dass jeder Schnittpunkt
zweier Diagonalen diese im Goldenen Schnitt teilt. |
In Grabbauten wird oft ein Himmel
aus fünfzackigen Sternen auf blauem Grund dargestellt.
4
....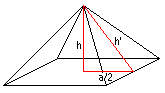 .. .. |
Für das rote Dreieck gilt die Proportionenkette
h' : h : a/2 = 5 : 3,90 : 3,11. Das ist angenähert
5 : 4 : 3.
Für diese Zahlen gilt 5² = 4² + 3².
Sie sind damit pythagoräische Zahlen.
Vermutung: Das Dreieck in der Pyramide ist ein pythagoräisches
Dreieck. |
Mit einer 3-4-5-Knotenschnur
wurden angeblich im alten Ägypten nach der jährlichen Nilschwemme
die Felder neu vermessen. Mehr über die Knotenschnur findet man auf
meiner Seite
3-4-5-Dreieck.
5
...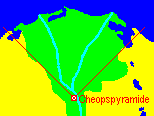 ... ... |
Das Grundquadrat ist genau nach den Himmelsrichtungen
ausgerichtet.
Verlängert man die Diagonalen des Grundquadrates,
so schließen die Verlängerungen das Nildelta ein. |
Die Lage der Cheopspyramide
ist bemerkenswert, zumal man von ihr auch weit in das Nildelta hineinsehen
kann, falls es der Smog von Kairo zulässt.
6
...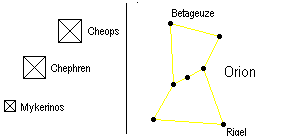 ... ... |
Die Cheopspyramide steht nicht isoliert da und bildet
mit den Pyramiden des Chephren und des Mykerinos eine fast gerade Linie.
Eine ähnliche Anordnung haben (besser hatten vor 4500 Jahren) die
drei Gürtelsterne im Sternbild des Orion. Außerdem gibt es noch
zwei Pyramiden am Nilufer, die zwei Randsternen des Orion entsprechen (Quelle:
Robert Bauval, zitiert in einer ZDF-Sendung). |
7
Welche Form hat eine Pyramide,
die das Volumen und den Mantel mit der Großen Pyramide von Gizeh
gemeinsam hat?
Lösung: Die Rechnung führt
zur kubischen Gleichung
h³ - (M²/12/V)*h²
+ (3/4)*V = 0.
Mit V=2646000 und M=87120 erhält
man die Lösungen h1=146,6 und h2=171,4 und h3= -79,0 (gefunden mit
DERIVE).
......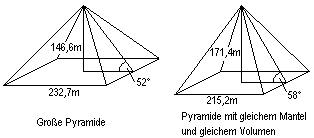 |
Die Höhe h2=171,4m ist die zweite Lösung.
Zur Höhe h2 gehört die Quadratseite a2=215,2m. |
Dieses ist kein neuer Beitrag zur Pyramidenforschung,
nur eine kleine Spielerei.
Zusammenfassung
Es steht fest, dass die alten Ägypter die Maße
der Pyramiden so gewählt haben, dass sie stabil und ansehnlich wurden.
Wer weiß?
Vielleicht sind darüber hinaus in den Pyramiden
geheimnisvolle Gesetze verborgen.
Andererseits: Zahlen sind geduldig... Zu dieser Meinung
neige ich als Skeptiker mehr.
Die Kraft der
Pyramiden top
In der amerikanischen Wissenschaftszeitung
"Scientific American" vom Juni 1974 berichtete ein Dr. Matrix von einer
Kraft, die von der Pyramide ausgehe. In Modellen einer Pyramide würden
seltsame Dinge geschehen: Rasierklingen würden wieder scharf, Fleisch
verwese deutlich langsamer und eine Person erfahre in einer Pyramide sitzend
eine Steigerung der übersinnlichen Fähigkeiten und mehr. Diese
Aussagen wurden durch Berichte aus aller Welt belegt und erschienen glaubhaft.
Stopp ;-) !
Es handelte sich hierbei um einen wissenschaftlichen Spaß,
mit dem die Sucht nach Übernatürlichem persifliert wurde. - Hinter
dem Pseudonym Dr. Matrix verbarg sich der bekannte Wissenschaftsjournalist
Martin Gardner von "Scientific American".
Mich interessiert, ob man sich schon vor 1974 in Pyramiden
setzte
;-).
Pyramiden im Internet
top
Deutsch
Frank Dörnenburg
Rätselhafte
Pyramiden
Ingrid Huber
Grundwissen
über Pyramiden
Wikipedia
Pyramide
(Geometrie), Tetrakishexaeder,
Pyramidenzahl,
Pyramide
(Bauwerk),
Pyramiden
von Güímar
Unter Leitung des Ethnologen Thor Heyerdahl entstand
in Teneriffa ein Pyramiden-Museum. Es wird die (umstrittene) Theorie belegt,
dass es einen Zusammenhang zwischen den Pyramiden in Ägypten und in
Mittelamerika gibt. Trotzdem: Ein interessantes und geschmackvoll eingerichtetes
Museum.
Englisch
Andrew Bayuk (Guardian's CyberJourney To Egypt)
The
Great Pyramid
Edward Furey (Southborough Website Design)
Square
Pyramid Calculator
Eric W. Weisstein (MathWorld)
Pyramid,
Square
Pyramid,
Square
Pyramidal Number
Gijs Korthals Altes
Paper
Models of Square Pyramids
Kevin Matthews and Artifice, Inc. (greatbuildings.com)
Sources
on Great Pyramid of Khufu, Pyramide
du Louvre
Lee Krystek
Khufu's
Great Pyramid
Tim Hunkler
The Great
Pyramid as Proof of God
Wikipedia
Pyramid
(geometry), Pyramid
number, Tetrakis
hexahedron, Pyramid,
The
Pyramids of Guimar
Referenzen top
(1) Lancelot Hogben: Die Entdeckung der Mathematik, Stuttgart
1963
(2) Martin Gardner: Die magischen Zahlen des Dr. Matrix,
Frankfurt am Main 1987
(3) Armando Curcio (Hrg.): Meilensteine der Archäologie,
Herrsching 1987
(4) David Blatner: Pi, Magie einer Zahl, Reinbek bei
Hamburg 1997
(5) FTI Touristik Publications: Reisebegleiter Ägypten,
2000?
(6) "Gibt es ein Geheimnis der Pyramiden?"
Zwei Fernsehfilme aus der Reihe "Querschnitt" von Hoimar von Ditfurth,
ZDF (gesendet am 29.03.1976 und am 05.04.1976, im Jahre 1991 wiederholt)
Diese beiden Fernsehfilme waren auch eine Reaktion
auf Erich von Dänikens damaligen Bestseller "Erinnerungen an die Zukunft"
mit der Spekulation: "Die Pyramiden sind mit dem Wissen Überirdischer
gebaut worden".
Die Antwort gab der Film: "Die Ägypter konnten
die Pyramiden
aus eigener Kraft bauen."
Die beiden Filme waren in der wissenschaftlichen Beweisführung
vorbildlich: In der ersten Sendung wurden nur Fakten zusammengetragen.
In der zweiten Sendung wurden sie entweder bewiesen, oder es wurden vorsichtig
mögliche Erklärungen angeboten, die der Fernsehzuschauer bewerten
konnte.
Ach so, meine Homepage heißt
Mathematische
Basteleien:
Kommentar top
Diese Webseite habe ich unter dem Eindruck einer Ägyptenreise
mit der Besichtigung der Pyramiden im April 2001 angefertigt.
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist ohne die Erweiterung 2011 auch in Englisch
vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2001 (erweitert 2011) Jürgen Köller
top |


 ...
... ...
... ...
... ...
... ...
... ...
...




 ...
...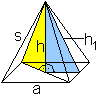 ...
... ...
... ...
... ...
... ....
....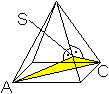 ...
...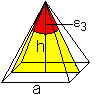 ...
...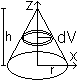 ...
... ...
...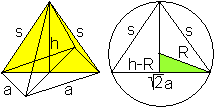 ...
...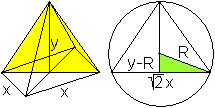
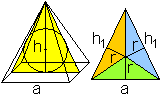 ...
...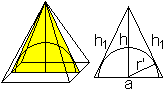 ...
... ...
...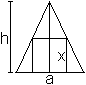 ...
... ...
... ...
...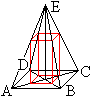 ...
...


 ...
... ...
... ...
... ...
...
 ...
... ...
... ...
...
 ...
... ...
... ..
.. ...
... ...
...