Pyramidenstumpf

Inhalt dieser Webseite

Was ist ein Pyramidenstumpf?
Größen
Besondere Pyramidenstümpfe

Pyramidenstümpfe mit persönlichem Bezug
Pyramidenstumpf im Internet
Referenzen.

Zur Hauptseite "Mathematische Basteleien"

Was ist ein Pyramidenstumpf?

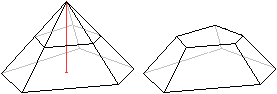...... Legt man durch eine Pyramide eine Schnittebene parallel zur Grundfläche, so entsteht ein Pyramidenstumpf.
Die abgeschnittene Pyramide ist zur Ausgangspyramide ähnlich und heißt Ergänzungspyramide.

Der Pyramidenstumpf hat eine Grundfläche, eine Deckfläche und Seitenflächen, die zusammen den Mantel bilden.
Der Abstand von Grund- und Deckfläche ist die Höhe.

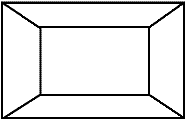
Aufsicht

...

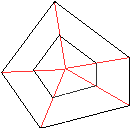Von oben gesehen erkennt man, dass Grund- und Deckfläche ähnliche Vielecke sind.

Das Vieleck kann ein Dreieck, Viereck, ..., n-Eck sein. Hier ist n=5.

Bekannt sind die Pyramidenstümpfe, bei denen die Vielecke regelmäßig sind.

Seitenansicht

...

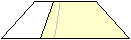Die Seitenflächen sind Trapeze, die aber in dieser Ansicht verzerrt dargestellt werden.

Größen top
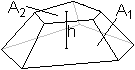
Die Grundfläche sei ein n-Eck mit dem Flächeninhalt A₁. Die Deckfläche habe den Flächeninhalt A₂. Der Mantel sei M. Die Höhe sei h.
Dann lassen sich aus diesen vier Größen die Oberfläche und das Volumen berechnen.

...... O= A₁+ A₂ + M
V=(1/3)h[A₁+sqrt(A₁A₂)+A₂]

Zur Herleitung der Volumenformel

...

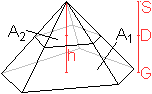GD=h sei die Höhe des Pyramidenstumpfes, h₁=GS die der Ausgangs- und h₂=DS die der Ergänzungspyramide.
Das gesuchte Volumen V ergibt sich als Differenz V=(1/3)A₁h₁-(1/3)A₂h₂.

Wegen der parallelen Schnittflächen gilt die Proportion A₁:A₂ =h₁²:h₂² oder h₁:h₂=sqrt(A₁):sqrt(A₂).
Berücksichtigt man noch h=h₁-h₂, so ergibt sich h₁=h*sqrt(A₁)/[sqrt(A₁)-sqrt(A₂)] und h₂=h*sqrt(A₂)/[sqrt(A₁)-sqrt(A₂)].
Für das Volumen V=(1/3)A₁h₁-(1/3)A₂h₂ erhält man dann nach längerer Rechnung V= (1/3)h[A₁+sqrt(A₁A₂)+A₂], wzbw..

Faustregel
Die unhandliche Formel V= (1/3)h[A₁+sqrt(A₁A₂)+A₂] ersetzt man gerne durch die einfache Faustformel V'=(1/2)h(A₁+A₂).
Dazu gibt es eine Fehlerbetrachtung.
V'-V =(1/2)h(A₁+A₂)-(1/3)h[A₁+sqrt(A₁A₂)+A₂]=...=(1/6)h[A₁+A₂-2sqrt(A₁)sqrt(A₂)]=(1/6)h[sqrt(A₁)-sqrt(A₂)]².
Der Fehler ist Null, wenn A₁=A₂ gilt.
Der Fehler ist also um so kleiner, je mehr sich der Pyramidenstumpf einem Prisma nähert.

Besondere Pyramidenstümpfe top
Gerader dreiseitiger Pyramidenstumpf
Grund- und Deckfläche sind gleichseitige Dreiecke.

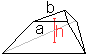...... Gegeben seien die Dreiecksseiten a und b und die Raumhöhe h.
Die Formeln für das Volumen und die Oberfläche lauten V=(1/12)sqrt(3)h(a²+ab+b²) und O=(1/4)sqrt(3)(a²+b²)+(1/4)(a+b)sqrt[36h²+3(a-b)²]}

Herleitungen
V=(1/3)h[A₁+sqrt(A₁A₂)+A₂]=(1/3)h[(1/4)sqrt(3)a²+sqrt{[(1/4)sqrt(3)a²*(1/4)sqrt(3)b²]}+(1/4)sqrt(3)b²]
=(1/3)h[(1/4)sqrt(3)a²+(1/4)sqrt(3)ab+(1/4)sqrt(3)b²]=(1/12)sqrt(3)h(a²+ab+b²), wzbw.

...

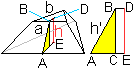Zur Berechnung der Oberfläche benötigt man die Höhe h' der Trapeze, die den Mantel bilden.
Es gilt h'² = h²+AC² = h²+(AE-BD)² = h²+{(1/3)(1/2)sqrt(3)a-(1/3)(1/2)sqrt(3)b}² = h²+(1/12)(a-b)]² oder h'=sqrt[h²+(3/36)(a-b)²]=(1/6)sqrt[36h²+3(a-b)²].

O=A₁+A₂+M = (1/4)sqrt(3)a²+(1/4)sqrt(3)b²+3*(1/2)(a+b)h' = (1/4)sqrt(3)(a²+b²)+(1/4)(a+b)sqrt[36h²+3(a-b)²] wzbw.
Nach (1), Seite 460 ff.

Gerader quadratischer Pyramidenstumpf
In diesem Sonderfall ist die Ausgangspyramide eine gerade, quadratische Pyramide.
Grund- und Deckfläche sind Quadrate.

...

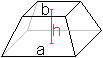Gegeben seien die Quadratseiten a und b und die Raumhöhe h.
Die Formeln für das Volumen und die Oberfläche lauten V=(1/3)h(a²+ab+b²) und O=a²+b²+(a+b)sqrt[4h²+(a-b)²]

Herleitungen
Volumen
V=(1/3)h[A₁+sqrt(A₁A₂)+A₂]=(1/3)h(a²+ab+b²)

...

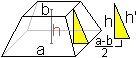Zur Berechnung der Oberfläche benötigt man die Höhe h' der Trapeze, die den Mantel bilden.
Es gilt h'²=h²+[(a-b)/2]² oder h'=sqrt[h²+(1/4)(a-b)²]=(1/2)sqrt[4h²+(a-b)²].

Oberfläche
Dann ist O =A₁+A₂+M = a²+b²+4*[(1/2)(a+b)h'] = a²+b²+4*{(1/2)(a+b)(1/2)sqrt[4h²+(a-b)²]} = a²+b²+(a+b)sqrt[4h²+(a-b)²]

Kegelstumpf
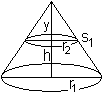
Der Kegelstumpf ist ein Grenzfall des Pyramidenstumpfes mit regelmäßigem Grund- und Deckkreis.
Die Anzahl der Ecken geht über alle Grenzen. Es ergibt sich dann ein Kreis.

...

...DD

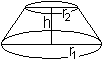
Der Kegelstumpf wird im Allgemeinen durch die Höhe h und die Radien r₁und r₂ von Grund- und Deckkreis gegeben.
Das Volumen des Kegelstumpfes ist dann V=(1/3)pi*h( r₁²+ r₁r₂+r₂²).

...

Mehr findet man auf meiner Kegel-Seite.

Obelisk
Ein Obelisk ist eine freistehender, hoher, sich nach oben verjüngender, rechteckiger Steinpfeiler, der eine pyramidenförmige Spitze hat. (nach Wikipedia).

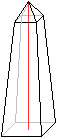Anders ausgedrückt: Der Obelisk ist er ein gerader, quadratischer Pyramidenstumpf mit aufgesetzter Pyramide, wobei die Höhe wesentlich größer als die Kante der Grundfläche ist. Außerdem ist die Deckfläche nicht wesentlich kleiner als die Grundfläche.

Pyramidenstümpfe mit persönlichem Bezug top
John Hancock Center in Chicago

...... Das John Hancock Center hat die Form eines Pyramidenstumpfes (Mitte, hinten).
Die Aufnahme entstand im September 2005 auf der Aussichtsterrasse des Sears Towers im Abendlicht.
Die Form wird besonders deutlich, wenn man sich das Gebäude in der Aufsicht bei Google Earth ansieht. Es genügt, mit "John Hancock Center" zu suchen (Rechts eine maßstabgetreue Skizze).
Mehr unter
http://en.wikipedia.org/wiki/John_Hancock_Center

......