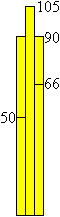|
Was ist ein Prisma?
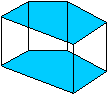
Gerades Prisma
... ... ...
|
Verschiebt man ein beliebiges Vieleck längs der
Flächennormalen parallel im Raum, so entsteht ein Prisma.
Dieser Körper ist im engeren Sinne ein Prisma und
heißt genauer
gerades Prisma. |
Schiefes
Prisma
... ... ...
|
Ist die Richtung der Verschiebung nicht senkrecht zur
Grundfläche, so entsteht ein schiefes Prisma. |
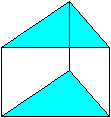
Dreiseitiges
Prisma und quadratisches Prisma
... ... ... |
...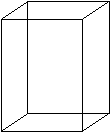 ... ... |
Unter den Prismen gibt es solche, die Dreiecke oder Quadrate
als Grundflächen haben.
Sie heißen dreiseitiges (gerades) Prisma
oder quadratisches (gerades) Prisma. |
Zylinder
...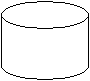 ... ... |
Es ist die Frage, ob man auch die Zylinder zu den Prismen
zählt.
Das ist zwar nicht üblich, kann man aber tun. |
Früher hieß das
Prisma auch Säule. Dieser Begriff ist aus den Lehrbüchern der
Mathematik verschwunden.
Auf dieser Seite geht es
um das dreiseitige und das quadratische Prisma.
Was
ist ein dreiseitiges Prisma?
top
Das dreiseitige Prisma heißt manchmal auch Dreieckprisma
oder Dreiecksäule.
...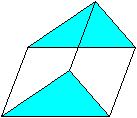 ... ... |
Verschiebt man ein beliebiges Dreieck parallel im Raum,
so bilden die Punkte im Bereich der Verschiebung ein dreiseitiges Prisma.
Es besteht aus zwei kongruenten Dreiecken, deren Eckpunkte
passend miteinander verbunden sind. Dadurch entstehen drei Parallelogramme,
die Seitenflächen. Die Dreiecke heißen Grundflächen oder
anschaulicher Grund- und Deckfläche. Der Abstand der Dreiecke ist
die Höhe des Prismas.
Die Bezeichnung "dreiseitig" bezieht sich auf die Grundfläche,
das Prisma ist "neunkantig". |
Dreiseitiges,
gerades Prisma
... ... ... |
Wird ein Dreieck senkrecht zu seiner Fläche (d.h.
in Richtung der Normalen der Grundfläche) verschoben, so entsteht
ein gerades Prisma. Die Seitenflächen werden zu Rechtecken.
Das Prisma oben nennt man schief. |
Regelmäßiges,
dreiseitiges, gerades Prisma
... ... ...
|
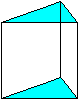
Sind die Dreiecke gleichseitig, so ist das Prisma auch
noch regelmäßig. |
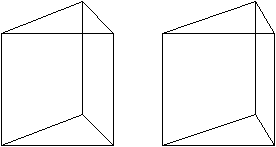
Wer den 3D-Blick beherrscht, sieht ein gerades Prisma
räumlich.
Gleichkantiges
Prisma top
Damit ist ein regelmäßiges,
dreiseitiges, gerades Prisma mit gleich langen Kanten gemeint.
Darstellung
... ... ...
|
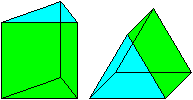
In zwei Schrägdarstellungen (k=1/2, alpha=45°)
wird das Quadrat und rechts das gleichseitige Dreieck originalgetreu dargestellt.
Das Prisma besteht aus drei Quadraten und zwei gleichseitigen
Dreiecken. |
Schneidet man den Körper an
den Kanten auf, so erhält man ein Netz. Es gibt neun verschiedene
Netze.

Größen
Das sind die Seitenlänge des
Dreiecks a, die Höhe h=a, das Volumen V, der Mantel M und die
Oberfläche O.
...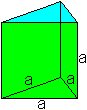 ... ... |
Ist die Kantenlänge a gegeben, so lassen sich die
übrigen Stücke berechnen:
V=sqrt(3)/4*a³, M=3*a² und O=[sqrt(3)/2+3]*a².
Das Prisma hat e=6 Ecken, k=9 Kanten und f=5 Flächen.
Es gilt die eulersche Polyedersatz e+f-k=2. |
Mittelpunkt
und Umkugel
...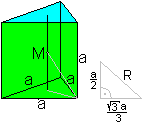 ... ... |
Verbindet man die Mittelpunkte der beiden Dreiecke, so
liegt in der Mitte dieser Strecke der Mittelpunkt M des Prismas. Dieser
Punkt hat von allen Eckpunkten des Prismas die gleiche Entfernung. Somit
ist er der Mittelpunkt der Umkugel.
Nach dem Satz des Pythagoras ist R=sqrt(21)/6*a. Das ist
0,76*a |
Keine Inkugel
...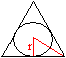 ... ... |
Eine Kugel, die alle 6 Flächen innen berührt,
gibt es nicht. Begründung:
Der Radius einer möglichen Inkugel müsste nach
nebenstehender Zeichnung r=h'/3=sqrt(3)/6*a sein. Andererseits hat das
Prisma die Höhe a. Danach wäre r=a/2. Das ist ein Widerspruch. |
Größtes
regelmäßiges dreiseitiges Prisma top
...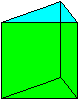 ... ... |
Die Frage ist, welche Form ein regelmäßiges,
dreiseitiges Prisma hat, dessen Volumen maximal ist und dessen Oberfläche
vorgegeben wird. |
Die Antwort gibt eine Rechnung.
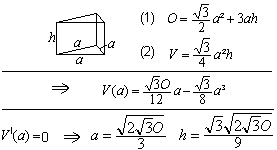
|
Ergebnis:

|
Es ist erstaunlich:
Dieselbe Form hat ein regelmäßiges, dreiseitiges
Prisma, wenn bei festem Volumen die Oberfläche maximal ist.
Schnitte durch
ein Prisma
top
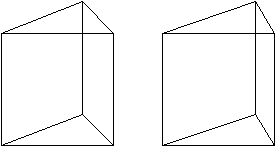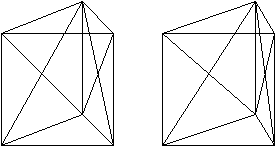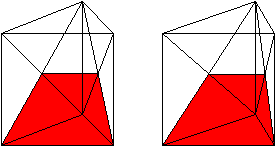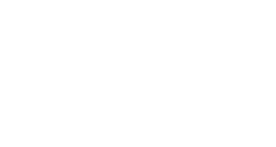
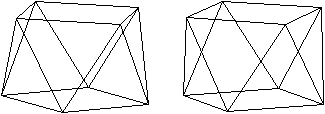
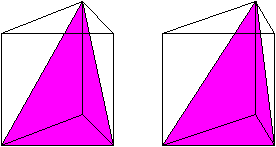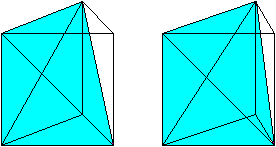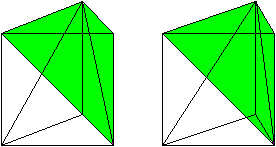
Man verbindet die beiden hinteren Eckpunkte eines Prismas
mit den gegenüberliegenden vorderen Eckpunkten. Es entstehen zwei
Dreiecke, die Schnittebenen durch das Prisma kennzeichnen. Der (rote) Restkörper
unten ist eine Pyramide mit einem Viereck als Grundfläche.
Diese Pyramide wird vom ersten Schnittdreieck gebildet,
wenn es an seiner Mittellinie nach hinten umgeklappt wird.
Verbindet man den oberen hinteren Eckpunkt mit den beiden
unteren Eckpunkten, so entsteht ein (violettes) Dreieck. Dieses Dreieck
ist Grundfläche einer Pyramide, die im hinteren Eckpunkt unten ihre
Spitze hat.
Zeichnet man zum Viereck vorne eine Diagonale, so kann
man zwei weitere Pyramiden entdecken. Das Besondere ist, dass die drei
Pyramiden das Prisma ausfüllen und das gleiche Volumen haben.
Dreiseitige
Prismen um uns
top
Hört man den Namen Prisma, so denkt man am ehesten
an das Glasprisma, mit dem man weißes Licht zerlegen kann.
...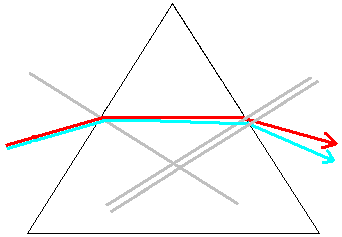 ... ... |
Sendet man ein schmales Lichtbündel weißen
Lichts in ein Prisma, so wird das Licht beim Übergang von Luft nach
Glas zum Lot hin gebrochen. Beim Übergang von Glas zu Luft wird das
Licht vom Lot weg abgelenkt.
Das Besondere ist, dass die Brechung des Lichts von der
Farbe abhängt. Zum Beispiel wird blaues Licht stärker gebrochen
als rotes. In der Zeichnung wird der Unterschied zur Verdeutlichung übertrieben.
Das weiße Licht wird in die Spektralfarben zerlegt.
Es entsteht ein Spektrum.
In ähnlicher Weise zerlegen Wassertropfen manchmal
das weiße Sonnenlicht und erzeugen einen Regenbogen. |
Im Unterschied zu anderen Körpern
ist das dreiseitige Prisma nicht sehr verbreitet. Mir fallen als Stichworte
ein:
Axt oder Beil, BOC Tower in Hongkong, Bucheckern, Flat-Iron
House in New York, Kaleidoskop, Keil, Satteldach, Toblerone-Packung, Umkehrprisma,
Zelt.
Über Antiprismen findet man einiges auf meiner Deltaeder-Seite.
Was
ist ein quadratisches Prisma? top
... ... ... |
Ein Quader mit zwei quadratischen Seitenflächen
heißt auch
quadratisches Prisma.
Ein anderer Name ist regelmäßiges, vierseitiges
Prisma.
Die alte Bezeichnung quadratische Säule ist
aus den Lehrbüchern der Mathematik weitgehend verschwunden. |
Wer den 3D-Blick beherrscht, sieht das Prisma räumlich.
... |
Auch der Würfel ist ein quadratisches Prisma. |
Größen
des Prismas top
Das Prisma sei durch die Grundkante a und die Höhe
h gegeben.
...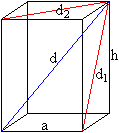 ... ... |
Dann sind die Längen der Flächendiagonalen
d1=sqrt(a²+h²) und d2=sqrt(2)*a.
Die Raumdiagonale hat die Länge d=sqrt(d1²+a²)=sqrt(2a²+h²).
Die Oberfläche ist O=2a²+4ah und das Volumen
V=a²h. |
Größte Prismen
top
Prisma größten Volumens
...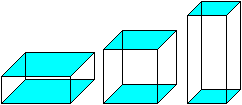 ... ... |
Die nebenstehenden quadratischen Prismen haben die gleiche
Oberfläche, aber unterschiedliche Formen.
Man erkennt vielleicht, dass der Würfel in der Mitte
das größte Volumen hat. |
Das zeigt die folgende Rechnung.
Nebenbedingung: O=2a²+4ah oder h=(O-2a²)/(4a)
Zielfunktion: V=a²h oder V(a)=a²(O-2a²)/(4a)=Oa/4-a³/2
Es gilt V'(a)=O/4-3a²/2. V'(a)=0
ergibt O/4-3a²/2=0 oder a=sqrt(O/6)=sqrt(6O)/6.
Dann ist h=(O-2a²)/(4a)=sqrt(6O)/6.
Es gilt also a=h. Damit ist das Prisma ein Würfel.
Dem
Würfel kann man sich auch aus einer anderen Richtung nähern.
Prisma
größter Oberfläche top
Es stellt sich weiter die Frage nach dem Prisma größter
Oberfläche, wenn das Volumen konstant gehalten wird.
Auch da ist der Körper ein Würfel, wie die
folgende Rechnung zeigt.
Nebenbedingung: Es gilt V=a²h oder h=V/a².
Zielfunktion: O=2a²+4ah oder O(a) =2a²+4V/a.
Es gilt O'(a)=4a-4V/a²
O'(a)=0 ergibt 4a³-4V=0 oder a=V1/3 . Dann ist h=V/a²=V/V2/3
=V1/3
Es gilt also a=h. Damit ist auch hier das Prisma ein
Würfel.
Eine
Schachtel größten Volumens top
...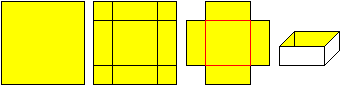 ... ... |
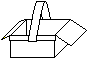
Gegeben ist ein quadratisches Stück Papier.
Man entfernt an den Ecken vier Quadrate, so dass ein Kreuz
entsteht. Aus dem Kreuz faltet man eine oben offene Schachtel. |
Die Frage ist, wie groß die Eckquadrate sein müssen,
damit das Volumen möglichst groß ist.
Die Antwort gibt eine Rechnung.
...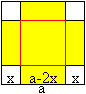 ... ... |
Zielfunktion: V(x)=(a-2x)²x=4x³-4ax²+a²x
Die erste Ableitung ist V'(x)=12x²-8ax+a².
V'(x)=0 ergibt 12x²-8ax+a²=0 oder x²-2ax/3+a²/12=0.
V''(x)=-8a+24x.
Diese quadratische Gleichung hat die Lösungen
x1=a/6 und x2=a/2.
Für x2=a/2 gibt es keine Schachtel. Die
Lösung ist x1=a/6 oder (a-2 x1)=2a/3.
Mit V''(a/6)= - 4a<0 ist sichergestellt, dass ein
Maximum vorliegt.. |
Ergebnis: Die Schachtel hat die Kanten a/6, 4a/6 und 4a/6.
Das ist das Verhältnis 1:4:4
Größtes
Prisma in der quadratischen Pyramide top
...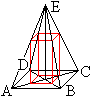 ... ... |
Gegeben sei eine quadratische Pyramide durch die Grundkante
S und die Höhe H .
Gesucht wird ein quadratisches Prisma in der Pyramide
mit dem größten Volumen.
Für eine Rechnung betrachtet man einen Schnitt durch
die Punkte A, C und E |
Rechnung
...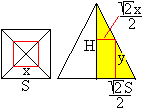 ... ... |
Die Grundseite des Prismas sei x und die Höhe sei
y.
Dann gilt nach dem zweiten Strahlensatz:[sqrt(2)S/2]
:
[sqrt(2)x/2]=H
:
(H-y) oder y=H-(H/S)x.
Zielfunktion: V=x²y oder V(x)=x²[H-(H/S)x]=Hx²-(H/S)x³
V'(x)=2Hx-3(H/S)x². V'(x)=0 ergibt 2Hx-3(H/S)x²=0
mit den Lösungen x1=0 und x2=2S/3.
Für x1=0 existiert kein Prisma.
Zu x2=2S/3 gehört y2=H-(H/s)x2=H/3 |
Ergebnis: Das Prisma mit der Grundseite (2/3)S und der Höhe
(1/3)H hat das größte Volumen.
Ist H=S, so ist das Prisma ein halber Würfel.
Zwei
besondere Quader top
...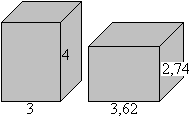 ... ... |
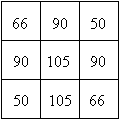
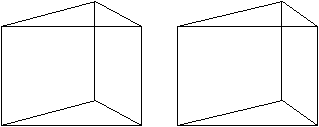
Die beiden nebenstehenden Prismen haben unterschiedliche
Grundseiten und Höhen und damit unterschiedliche Formen, aber die
Volumina und die Oberflächen sind gleich.
Es gilt für den linken Körper V=3²*4=36
und O=2*3²+4*3*4=66.
Für den rechten Körper gilt V=3,62²*2,74=36
und O=2*3,62²+4*3,62*2,74=66.
Allerdings sind Volumen und Oberfläche auf zwei
Stellen gerundet.
Unten stehen die genauen Maße. |
Die folgende Rechnung zeigt den Hintergrund.
Oben wurde die Gleichung V=Oa/4-a³/2 hergeleitet.
Man kann sie auch als kubische Gleichung in a schreiben: a³-Oa/2+2V=0.
Es werden die Körper gesucht, für die V=36
und O=66 ist.
Das führt zur Gleichung a³-33a+72=0 oder (a-3)(a²+3a-24)=0
Diese Gleichung hat die Lösungen
a1=3, (Dazu gehört h1=4)
a2=sqrt(105)/2-3/2, ungefähr 3,62. Zu
a2 gehört h2=[144+3sqrt(105)]/64, ungefähr
h2=2,73.
a3= - sqrt(105)/2-3/2<0 (Keine
Lösung, eine negative Maßzahl ist nicht möglich.)
Diese Rechnung zeigt auch, dass nur die beiden
quadratischen Prismen oben das Volumen 36 und die Oberfläche 66 haben.
Wolkenkratzer
und Türme top
Wenn man darauf achtet, stellt
man fest, dass Hochhäuser und Türme sehr oft die Form eines quadratischen
Prismas haben.
Sears Tower in Chicago
Stellvertretend für Wolkenkratzer
mit quadratischem Grundriss wähle ich den Sears Tower in Chicago.
Durch ihn bin ich darauf gekommen, diese Seite über quadratische Prismen
zu machen.
Der Sears Tower besteht aus einem
Bündel von 3x3=9 Türmen, die unterschiedlich hoch sind.
Der Wolkenkratzer war von 1974
bis 1997 das höchste Gebäude der Welt.

Auch das hohe Aon Center rechts ist ein quadratisches
Prisma.
Jetzt kommt der Sprung von der Weltstadt
in die Provinz ;-).
Zwei
Kirchen in Bad Salzuflen
Stellvertretend für Kirchtürme wähle ich
aus meiner Heimatstadt die Stadtkirche in Bad Salzuflen und die Kilianskirche
in Schötmar.
In beiden Fällen haben die Kirchtürme einen
quadratischen unteren Aufbau und eine Bekrönung aus dem 19. Jahrhundert.
Die achtstrahligen Hauben passen zu einem quadratischen Turm.
Man begegnet Prismen an unterschiedlichen
Stellen meiner Homepage.
Prisma im Internet
top
Deutsch
Wikipedia
Prisma
(Geometrie), Willis
Tower
Englisch
Ask Dr. Math (The Math Forum)
Prism
Formulas
Eric W. Weisstein (MathWorld)
Prism,
Cuboid
John Rausch (Puzzle World )
Interlocking
- Double Triangular Prism
Tom Getty
Prisms
& Antiprisms
Wikipedia
Prism
(geometry)
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2009 Jürgen Köller
top |


 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
...
 ...
... ...
... ...
... ...
...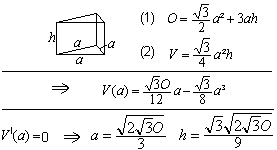


 ...
...

 ...
... ...
... ...
... ...
...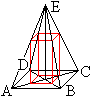 ...
...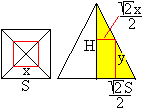 ...
... ...
...