Was ist ein Kaleidozyklus?
... ...
K1
|
Im einfachsten Falle versteht man unter einem Kaleidozyklus
einen Ring aus einer geraden Anzahl von Tetraedern. (Tetraeder
sind Pyramiden mit gleich langen Kanten und gleichseitigen Dreiecken als
Seitenflächen.)
Die Tetraeder sind an je zwei gegenüberliegenden
Kanten verbunden. Diese Kanten sind windschief und verlaufen senkrecht
zueinander.
Das Besondere ist, dass man diesen Ring ohne Ende in
sich drehen kann und dass sich dabei jede Pyramide von allen Seiten zeigt. |
Es gibt beliebig viele Kaleidozyklen. Die Tetraeder werden
dann meist zu Dreieckspyramiden.
Auf dieser Seite werden der Reihe nach besondere Kaleidozyklen
vorgestellt und beschrieben.
Sie werden mit K1 bis K14
bezeichnet.
Der Ring
aus acht Tetraedern
top
K2
Im
einfachsten Falle besteht der Ring aus acht Tetraedern.
... ... |
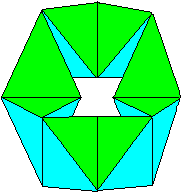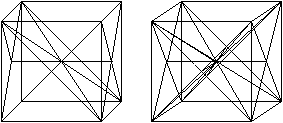
In der linken Zeichnung wird die Momentaufnahme eines
Ringes dargestellt, in der gemeinsame Kanten horizontal oder vertikal im
Raum stehen.
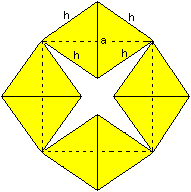
In der rechten Zeichnung wird ein Horizontalschnitt durch
die Mitte des Ringes gelegt. a ist die Kante eines Tetraeders, h ist die
Höhe eines Seitendreiecks.
Es gilt h=sqrt(3)/2*a.
Das gestrichelte Quadrat ist die Grundlage des Ringes. |
... ... |
Bau
des Ringes
Man kann den Ring ohne große Schwierigkeiten aus
Papier falten.
Man stellt aus Papier acht Tetraeder einzeln her und klebt
sie mit Tesafilm aneinander. Das ist einfach, aber mühsam.
Das ist übrigens für die Schule interessant
als Gemeinschaftsarbeit in einer Klasse.
Es ist geschickter, ein Netz des Ringes zu entwerfen.
Dann wird das Falten allerdings etwas knifflig. Aber keine Angst!
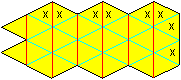
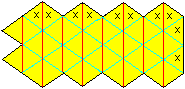
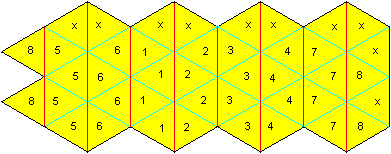(1) Man zeichnet mit Zirkel und Lineal die obenstehende Figur
aus gleichseitigen Dreiecken. Die Nummerierung und die Kennzeichnung der
Klebestellen mit x dienen nur der Erklärung.
Mit einer Seitenlänge eines Dreiecks von 2,5 cm
passt die Figur auf ein Blatt DINA4.
(2) Man schneidet die Figur aus.
(3) Damit man das Papier später gut falten kann,
muss man alle Linien mit einem leer geschriebenen Kugelschreiber nachziehen
und nach oben und unten vorknicken.
(4) Man formt zunächst die Tetraeder 1111 und 2222
gleichzeitig. Die Dreiecke xx oben und die Dreiecke 12 unten klebt man
zusammen.
(5) In der gleichen Weise verfährt man mit den Paaren
3333/4444, 5555/6666 und 7777/8888 in dieser Reihenfolge.
(6) Zum Schluss schließt man den Ring, indem man
die Dreiecke 88 links und xx rechts zusammenklebt.
Will man Ringe mit 10,12,14, ... Tetraedern basteln, muss
man weitere Streifen einschieben.
Geschlossener
Ring aus sechs Dreieckspyramiden top
K3
Versucht man, sechs Tetraeder ringförmig anzuordnen,
so reicht es nicht zu einem drehbaren Ring (Bild links). Man muss die Tetraeder
strecken, damit ein Ring zustande kommt. Der Grenzfall ist ein regelmäßiges
Sechseck die Querschnittfläche (Bild Mitte). Das führt zum Ring
rechts.
Es entsteht ein rechtwinkliges Dreieck mit den Seiten
b, a und a/2. Nach dem Satz des Pythagoras ist b²=a²+(a/2)²
oder b=sqrt(5)/2*a.
Aus den Tetraedern werden
Dreieckspyramiden.
... ...... |
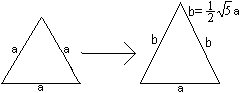Die Tetraeder bestehen dann nicht mehr aus gleichseitigen,
sondern aus gleichschenkligen Dreiecken. Das Verhältnis des Schenkels
zur Grundseite ist gleich
b : a = 1,12 : 1. |
Bastelvorlage
M.C.Escher
Kaleidozyklen
top
.. ... |
In dem unten genannten Buch (1) wird ein Ring aus gestreckten
oder gestauchten Tetraedern "der Kaleidozyklus" (Mehrzahl
die Kaleidozyklen, englisch kaleidocycle) genannt. Wegen der weltweiten
Verbreitung des Buches hat sich dieser Name durchgesetzt.
Der Name ist wohl aus dem Wort Kaleidoskop
(kaleidoscope) hergeleitet worden.
Das Buch enthält Bastelvorlagen und -anleitungen
für 14 Körper, darunter auch für etliche Ringe. |
Die Körper werden mit Motiven aus Bildern des holländischen
Malers M.C.Escher geschmückt und werden dadurch originell und ansehnlich.
Die geschlossenen Kaleidozyklen sind besonders faszinierend,
da die Rotation durch die Mitte mit viel Bewegung verbunden ist. Die Mitte
wird regelmäßig geöffnet und geschlossen.
Geschlossener
Ring aus acht Dreieckspyramiden top
K4
| ...... |
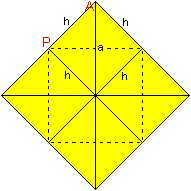
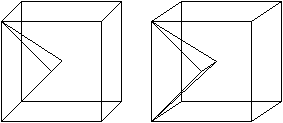
Wenn der Ring aus acht Tetraedern von oben kein Loch
mehr haben soll, muss man die Tetraeder so in der Form verändern,
dass das Loch wie im rechten Bild geschlossen wird.
Das führt zu einem Quadrat als Querschnittfläche.
Man muss sich den Ring so vorstellen, dass in den Seitenmitten des Quadrates
Kanten der Länge a senkrecht zur Zeichenebene liegen, so auch in Punkt
P. |
 ...... |
... ...E |
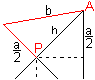
Klappt man in P die Kante a in die Zeichenebene, so ergibt
sich ein rechtwinkliges Dreieck, in dem man die Kante b der Pyramide berechnen
kann.
Es gilt b²=(a/2)²+h². Mit h=sqrt(2)/2*a
ergibt sich b=[sqrt(3)/2]a. |
Aus dem gleichseitigen Dreieck
des Tetraeders wird ein gleichschenkliges Dreieck.
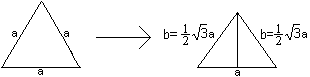Das Verhältnis des Schenkels zur Grundseite ist gleich
b : a = =0,87 : 1.
Bastelvorlage
Die Vorlage für einen
geschlossenen Ring aus 10 Pyramiden
K10 findet
man auf der Seite von Peupleur (Le Forum en Papier).
Der umstülpbare
Würfel
top
...
K5
Herstellung
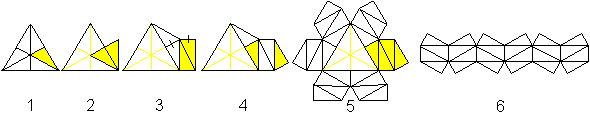(1) Zeichne ein gleichseitiges Dreieck mit ihren Mittellinien
(z.B. a=5cm)
(2) Spiegele ein Teildreieck an einer Seite.
(3) Errichte auf der Hypotenuse des gespiegelten Dreiecks
ein Rechteck. Die markierten Strecken sind gleich.
(4) Setze an das Rechteck das Teildreieck an. Die kleinere
Kathete liegt unten.
(5) Wiederhole diese Prozedur 5x. Aus den vier rechtwinkligen
Dreiecken wird eine Pyramide gefaltet.
(6) Bilde eine Reihe und bringe an die Dreiecke Klebestreifen
an, um die Pyramiden zu bauen und den Ring zu schließen.
Bastelvorlage
Ergebnis:
Es ist ein Kaleidozyklus aus sechs Pyramiden mit einem
dreieckigen Loch entstanden. Das Dreieck ist gleichseitig.
Beschreibung
... ... |
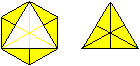Die Pyramiden stehen entweder auf einem gleichseitigen
Dreieck oder dem Rand eines regelmäßigen Sechsecks.
Vier Stellungen sind während des Drehens nach innen
bemerkenswert:
(1) Sechs Dreiecke der Pyramiden liegen in einer Ebene.
Sie erzeugen vorne ein hohles Sechseck.
(2) Man dreht weiter. Hinten bildet sich das gleiche
ebene Sechseck.
(3) Dann bilden sechs Dreiecke hinten ein ebenes Dreieck.
(4) Vorne entsteht danach ein ebenes Dreieck. |
Dieser Kaleidozyklus ist bekannt geworden als "umstülpbarer
Würfelgürtel nach Paul Schatz".
Es liegt nahe, den Namen
Würfelgürtel auf das bekannte Sechseck im Würfel zurückzuführen.
Es gelingt auch Dreiecksseiten innen und außen zu erkennen. Aber
die Pyramiden selbst kann ich auf diese Weise nicht in Beziehung zum Würfel
setzen.
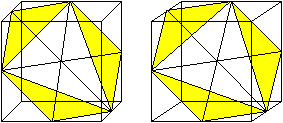
Wer den Stereoblick beherrscht, sieht sechs Grundflächen
der Pyramiden im Sechseck liegen.
Der Name Würfelgürtel ist so zu erklären.
Man kann den Ring so drehen, dass die rechten Winkel
der Dreiecke Würfelecken bilden:
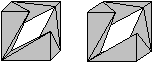
Man erkennt die sechs Pyramiden des Ringes, die allerdings
den Würfel nur zu einem Drittel ausfüllen.
Rechnung
dazu
... ... |
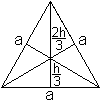Eine Pyramide wird aus jeweils vier Teildreiecken des
gleichseitigen Dreiecks gebildet. Ein Dreieck hat die Seiten a/2, h/3 und
2h/3, wobei die Höhe h des Dreiecks gleich h=[sqrt(3)/2]a ist. Der
Würfel hat dann die Kantenlänge a/2 und damit das Volumen V'=a³/8.
Die Pyramiden haben zusammen das Volumen 6*(1/3)*Grundfläche*Höhe. |
Das heißt hier V=6(1/3)[(1/2)(a/2)(h/3)][h/3]=(1/24)a³.
Also gilt V=V'/3.
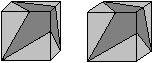
Will man den Würfel
zu einem Vollwürfel ergänzen, muss man zwei gleiche, dreigliedrige
Körper basteln, die man in den Drittelwürfel steckt.
Der Ring halbes
Oktaeder
top
K6
Die Öffnung ist ein Quadrat
Den Würfelgürtel kann
man weiterentwickeln zu einem Ring mit quadratischer Öffnung.
Herstellung
(1) Zeichne ein Quadrat mit den Diagonalen und den Mittellinien
(z.B. a=5cm).
(2) Spiegele ein Teildreieck an einer Seite.
(3) Errichte auf der Hypotenuse des gespiegelten Dreiecks
ein Rechteck. Die markierten Strecken sind gleich.
(4) Setze an das Rechteck das Teildreieck an.
(5) Wiederhole diese Prozedur 7x. Falte aus je
vier rechtwinkligen Dreiecken eine Pyramide.
(6) Bilde eine reihe und bringe an die Dreiecke Klebestreifen
an, um die Pyramiden zu bauen und den Ring zu schließen.
Bastelvorlage
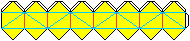
Dieser Ring heißt hier
"halbes Oktaeder".
Man kann nämlich die acht Pyramiden zu einem halben,
(roten) Oktaeder zusammenlegen.
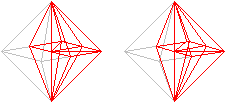
Quelle: Randolf Rehfeld.
Man erhält sicher weitere
geschlossene Kaleidozyklen, wenn man in ähnlicher Weise von höheren
regelmäßigen Vielecken ausgeht.
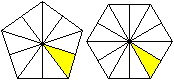
Doppelkrone top
K15
| ...... |
... ... |
Der Kaleidozyklus K6, der zu einem halben Oktaeder gefaltet
werden kann, hat eine quadratische Öffnung. Dreht man ihn weiter,
so kann man das Quadrat schließen und man erhält eine "Krone".
Diese Krone hat ein Quadrat als Grundfläche.
Da liegt es nahe, die Krone an der Grundfläche zu
spiegeln. |
... ... |
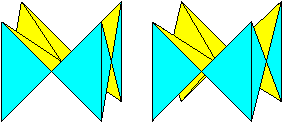
Das führt zu dem neuen Kaleidozyklus links, der
"Doppelkrone". Ein besserer Name fiel mir nicht ein. In dieser Lage erkennt
man, dass es eine Beziehung zu einem umfassenden Würfel gibt. Je zwei
Dreieckspyramiden bilden eine Kante des Würfels. |
Eine Rechnung zeigt, dass das Kaleidoskop den dritten Teil
des Würfels ausfüllt.
Der Würfel heißt
in dieser Aufteilung bei Margarita Ehrlich und Ellen Pawlowski (URL unten)
Schneider-Würfel.
durchsichtiger Würfel
|
eine Dreieckspyramide
|
4x
|
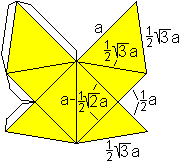
Als Vorlage können vier "Schmetterlinge" dienen
(a=5cm).
Aus jeder Figur ergibt sich eine Kante des korrespondierenden
Würfels.
Die Klebestreifen sind rechts nicht eingezeichnet. |
... ... |
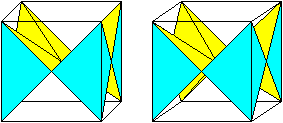
Der Kaleidozyklus Doppelkrone kann so gedreht
werden, dass wieder eine Krone mit quadratischer Grundfläche entsteht.
Die vier Zacken sind flacher.
Diese Krone kann man wieder am Quadrat spiegeln und schon
erhält man einen neuen Kaleidozyklus... |
Der halbe
geschlossene Ring aus sechs Dreieckspyramiden top
K7
Entstehung des hier abgebildeten
Ringes
... ... |
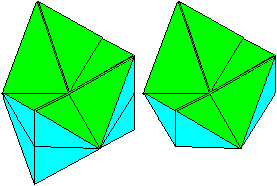Der geschlossene Ring aus sechs Dreieckspyramiden von
oben hat eine Symmetrieebene. Durch diese Ebene kann man einen Schnitt
legen. Es entsteht ein Kaleidozyklus, der sich über einem regelmäßigen
Sechseck erhebt.
Das Besondere ist, dass die gemeinsamen Kanten der Pyramiden
nicht mehr gleich lang sind. |
Dreht man den Ring weiter, so ergeben sich zwei besondere
symmetrische Stellungen des Ringes.
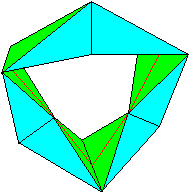
Die Öffnung ist ein gleichseitiges Dreieck (rot).
Die Silhouette ist ein gleichseitiges (nicht regelmäßiges)
Sechseck.
|
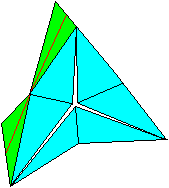
Der Silhouette ist ein gleichseitiges Dreieck (rot).
Der Ring ist fast geschlossen.
|
In beiden Fällen gibt es Symmetrieebenen durch das
rote Dreieck.
Das
Netz zum Bau dieses Kaleidozyklus sind sechs Quadrate mit aufgesetzten
gleichseitigen Dreiecken.
Die mit einen Strich gekennzeichneten
Strecken haben die Länge a, die mit zwei Strichen die Länge b=sqrt(5)/2*a
und die mit drei Strichen a/2.
Es besteht eine Verwandtschaft zum umstülpbaren Würfel
von oben. In beiden Fällen ist bei bestimmten Stellungen die Silhouette
ein Dreieck. Jedoch ist bei Schatz die Öffnung
geschlossen, in der symmetrischen Position oben rechts nicht: Die gemeinsame
Kante, die hier 0,5a lang ist, ist bei Schatz sqrt(3)/3*a=0,56a lang.
Dieser Ring soll eine Anregung
sein, nach neuen Kaleidozyklen zu suchen und sich mit ihnen zu beschäftigen.
Oben wurde schon erwähnt, dass es beliebig viele
Kaleidozyklen gibt.
Ein "normaler" Kaleidozyklus kommt immer dann zustande,
wenn "gegenüberliegende Kanten von Tetraedern und ihr gemeinsames
Lot paarweise senkrecht zueinander stehen" (Marcus Engel, kaleidozyklen_theorie.pdf).
The Shinsei Miracle
top
Dieser goldene/silberne Würfel wurde in den 1980er
Jahren von Naoki Yoshimoto entwickelt. Man kann ihn so auseinander nehmen,
dass man zwei Kaleidozyklen aus 12 Pyramiden erhält.
Mehr findet man auf meiner Seite The
Shinsei Miracle.
Cube One top
Cube One ist ein Würfel-Puzzle des Grafik-Designers,
Malers und Zeichners Dieter A.W. Junker aus Kassel.
Aufgabe des Puzzles ist es, aus 2x2 Kaleidozyklen einen
Würfel zusammenzusetzen.
Dabei ist schon jeder Kaleidozyklus
für sich ein Puzzle.
Aus dem einem kann man ein Tetraeder, aus dem anderen
ein Oktaeder bilden.
Mehr findet man auf meiner Seite Cube
One.
Tetra One top
Tetra One ist ein weiteres Puzzle
von Dieter A.W. Junker.
Aufgabe des Puzzles ist es, aus 2 Kaleidozyklen ein Tetraeder
zusammenzusetzen. Die beiden Kaleidozyklen unterscheiden sich nur in der
Reihenfolge der Pyramiden.
Mehr findet man auf meiner Seite Tetra
One.
Vorlagen top
Man findet auf dieser Seite Beschreibungen wie man ein
Netz zeichnen kann, um den betreffenden Ring zu basteln.
Doch es ist einfacher Vorlagen zu benutzen, die netterweise
im Internet bereitgestellt werden. Ich füge in der folgenden Linkliste
die Namen
Ki hinzu,
wenn man dort einen Bastelbogen findet.
Viel Spaß beim Basteln und auch bei der Suche nach
neuen Formen.
Kaleidozyklen
im Internet
top
Deutsch
Franz Zahaurek
Der umstülpbare Würfel
nach Paul Schatz
Randolf Rehfeld (Wundersames Sammelsurium)
Kaleidozyklen...K2,
K3, K4, K5, K6
Wikipedia
Umstülpbarer
Würfel
Englisch
Akira Nishihara
Ring
of tetrahedrons
Arvind Gupta
PAPER
FLEXAGON ENGLISH 20MB (Video bei Youtube)
David Singmaster
Cubic
Circular (magazine Issue 5 & 6 - #11 - #13) (Autumn &
Winter 1982)
Enchanted Learning online
Make
A 3-D Hexaflexagon ... K2
FoldPlay
MAKE
YOUR VERY OWN PHOTO KALEIDOCYCLE
G. Korthals Altes
Paper Models
of Polyhedra
Kaleidocycles: Hexagonal
Kaleidocycle K3, Octagonal
Kaleidocycle K2, Decagonal
KaleidocycleK1
Herbert Kociemba
Kaleidocycles
with 6 Disphenoids
instructables craft
Kaleidocycle
Jaap Scherphuis
Pyrix
(Chain of 4 octahedrons + 11 tetrahedrons = 1 large tetrahedron)
Maurice STARCK
a
ride through the polyhedra world
Paul Jackson
Origami
Hexaflexagon (Video bei Youtube)
Wikipedia
Kaleidocycle
Französisch
Peuplier (Le Forum en Papier)
Kaleïdocycle
didactique, le moteur 4 temps K4, Cube
magique, Shinsei Mystery (ou Miracle) K8
Referenzen top
(1) Doris Schattschneider und Wallace Walker, M.C.Escher
Kaleidozyklen, Köln 1992 K3,
K4
... ...
|
Verdrillter Kaleidozyklus K9 |
(2) Gerald Jenkins and Anne Wild, Make Shapes 1, Diss (Norfolk),
Tarqin Publications, 1998 K1
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2005 Jürgen Köller
top |
