Was ist das Haus des Nikolaus?
Das Haus des Nikolaus ist ein uraltes
(?) deutsches Zeichenspiel für kleine Kinder.
... ... ... |
Das Haus wird in einem Zug aus
acht Strecken gezeichnet.
Keine Strecke wird zweimal durchlaufen.
Während des Zeichnens spricht
man den Satz: "Das ist das Haus des Ni - ko - laus".
Zu jeder Strecke gehört ein
Wort bzw. eine Silbe. |
Man sagt auch:
"Das ist das Haus vom Nikolaus"
oder "Das ist ein wunderschönes Haus".
Mädchen sollten den Satz beachten:
"Wer dies nicht kann, kriegt keinen Mann" ;-).
|
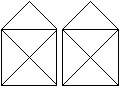
Auch für zwei Häuser nebeneinander gibt es
einen Spruch:
Das ist das Haus vom Ni-ko-laus
und ne-ben-an vom Weih-nachts-mann. |
... ... ...
|
Wer <N>ach-ge-<DACH>t <Z>uvor am Start,
der kennt den Weg von Le-on-hard! |
Eingesandt von Gerald Fischböck
aus Wien |
Anzahl
der Häuser top
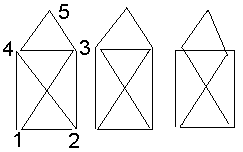
Drei Beispiele
 ... ... |
Jeder, der das Haus kennt (Wer
kennt es nicht?), kann mindestens ein Haus zeichnen, weil er sich einen
Streckenzug gemerkt hat.
Die Frage ist: "Wie viele Möglichkeiten gibt es das
Haus zu zeichnen? |
Aufschreiben
einer Lösung
Zum Aufschreiben einer Lösung
empfiehlt sich eine Ziffernfolge. Die Ecken
des Hauses werden durchnummeriert, zum Beispiel so: Unten links liegt die
Ecke 1. Die Ziffern 2, 3 und 4 folgen entgegen dem Uhrzeigersinn
für die Ecken des Rechtecks. Die Spitze erhält die Ziffer 5.Die
oben gezeichneten Häuser haben dann die Darstellungen 142354312,
145321342, 143213542. Eine Lösung kann
also durch eine neunstellige Zahl angegeben werden.
Es gibt 44
Häuser
Ein Computerprogramm (C64-Nostalgie!)
prüfte alle neunstelligen Zahlen zwischen 111111111 bis 155555552,
ob sie eine Lösung darstellen. Es ergaben sich die folgenden 44 Lösungen.
1,2,3,1,4,3,5,4,2
1,2,3,5,4,3,1,4,2
1,2,4,5,3,1,4,3,2
1,3,2,4,5,3,4,1,2
1,3,4,2,3,5,4,1,2
1,3,5,4,2,1,4,3,2
1,4,2,1,3,5,4,3,2
1,4,3,2,1,3,5,4,2
1,4,5,3,1,2,4,3,2
|
1,2,3,1,4,5,3,4,2
1,2,4,1,3,4,5,3,2
1,2,4,5,3,4,1,3,2
1,3,4,1,2,3,5,4,2
1,3,4,5,3,2,1,4,2
1,3,5,4,2,3,4,1,2
1,4,2,3,4,5,3,1,2
1,4,3,2,4,5,3,1,2
1,4,5,3,2,1,3,4,2
|
1,2,3,4,1,3,5,4,2
1,2,4,1,3,5,4,3,2
1,3,2,1,4,3,5,4,2
1,3,4,1,2,4,5,3,2
1,3,4,5,3,2,4,1,2
1,3,5,4,3,2,1,4,2
1,4,2,3,5,4,3,1,2
1,4,3,5,4,2,1,3,2
1,4,5,3,2,4,3,1,2
|
1,2,3,4,5,3,1,4,2
1,2,4,3,1,4,5,3,2
1,3,2,1,4,5,3,4,2
1,3,4,2,1,4,5,3,2
1,3,5,4,1,2,3,4,2
1,3,5,4,3,2,4,1,2
1,4,3,1,2,3,5,4,2
1,4,3,5,4,2,3,1,2
1,4,5,3,4,2,1,3,2
|
1,2,3,5,4,1,3,4,2
1,2,4,3,5,4,1,3,2
1,3,2,4,3,5,4,1,2
...
1,3,5,4,1,2,4,3,2
1,4,2,1,3,4,5,3,2
1,4,3,1,2,4,5,3,2
1,4,5,3,1,2,3,4,2
1,4,5,3,4,2,3,1,2
|
Alle Zahlenfolgen beginnen mit 1 und enden mit 2. Folglich
gibt es aus Symmetriegründen auch 44 Häuser, die in 2 beginnen
und in 1 enden. Sie sollten deshalb nicht als neue Lösungen angesehen
werden.
Alle Häuser
beginnen unten
In den Punkten 1 und 2 stoßen
drei Strecken aufeinander, in 3 und 4 vier Strecken, in 5 zwei Strecken.
Die Punkte 3 und 4 müssen
demnach zweimal Durchlaufstation sein, 5 einmal. In 1 und 2 ist eine Durchlaufstation
und eine Endstelle. Also müssen in 1 und 2 die Streckenzüge beginnen
oder enden.
Beginnt man an der Spitze in 5,
so müsste man auch in 5 enden. Das ist nicht möglich wegen der
ungeraden Streckenzahl in 1 und 2.
Eulerweg top
Das "Haus des Nikolaus" ist viel mehr als ein simples
Kinderspiel. Das zeigen die folgenden Ausführungen.
Es geht aus historischen Gründen zuerst um das Königsberger
Brückenproblem (Königsberg liegt an der Pregel, war vor 1945
die Hauptstadt Ostpreußens, gehört heute zu Russland und heißt
jetzt Kalingrad). Leonhard Euler (1707-1783) hat sich mit diesem Problem
beschäftigt und dabei den (heute so genannten) Eulerschen Satz aufgestellt.
...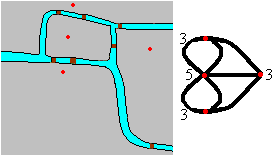 ... ... |
Das Problem besteht darin, dass man bei einem Rundweg
durch Königsberg alle sieben Brücken genau einmal überschreiten
soll. Ist das möglich?
Die Örtlichkeiten kann man zu einem Graphen aus vier
Punkten mit verbindenden Wegen vereinfachen. |
Euler behauptete, dass ein Rundgang vom Startpunkt und wieder
zurück zum Startpunkt wegen der ungeraden Anzahl von Wegen, die von
den Punkten ausgehen, nicht möglich ist. Nur wenn von jedem Kreuzungspunkt
aus eine gerade Anzahl von Wegen zusammenläuft, ist ein Rundweg, bei
dem jeder Weg nur einmal genommen wird, möglich. Das ist der Inhalt
des eulerschen Satzes. Ein Rundweg dieser Art heißt Eulerkreis. Ist
der Weg nicht geschlossen, so spricht man vom Eulerweg.
Das Königsberger Brückenproblem ist sozusagen
die Keimzelle eines neuen Zweiges der Mathematik geworden, der Graphentheorie
als Teil der Diskreten Mathematik.
... ... ... |
In der Fachsprache der Graphentheorie besteht das "Haus
des Nikolaus" aus fünf Knoten, die durch Kanten verbunden sind. Der
Graph ist planar, da die Kanten so gezeichnet werden können, dass
sie sich nicht kreuzen (Bild). Er ist nicht vollständig, da nicht
alle Knoten durch Kanten verbunden sind. |
Jeder Knoten hat einen Knotengrad. Das ist die Anzahl der
Kanten, die an einem Knoten zusammentreffen. Nach dem eulerschen Satz ist
es nicht möglich ist, einen Rundgang über alle Kanten zu machen,
da die unteren Punkte des Hauses den Grad 3 haben. Es gibt keinen Eulerkreis.
Wenn man aber unten in einem Punkt beginnt, kann man
alle Kanten einmal begehen und endet im Punkt unten auf der anderen Seite.
Ein Eulerweg ist möglich.
Hamiltonweg top
Es gibt ein zweites Problem, mit dem sich Euler beschäftigt
hat. Es geht nicht um Kanten, die einmal durchlaufen werden sollen, sondern
um Punkte, die nur einmal passiert werden dürfen. Diese Wege heißen
Hamiltonwege. Ist der Weg geschlossen, spricht man vom Hamiltonkreis.
Es gibt ein berühmtes Problem mit dem Hamiltonkreis,
die Springertour.
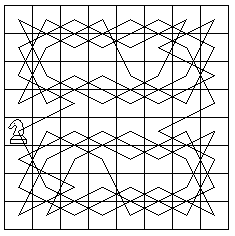 |
Der Springer soll sich auf einem Schachbrett so bewegen,
dass er jedes Feld nur einmal passiert und dass er zum Startpunkt zurückkehrt.
In der Sprache der Graphentheorie wird jetzt ein Weg
gesucht, bei dem jeder Knotenpunkt (das sind die Mittelpunkte der Quadrate)
genau einmal durchlaufen wird. Die Hamiltonwege benutzen immer zwei Kanten,
die an einem Knoten zusammen kommen.
Es gibt übrigens zum Springerproblem Tausende von
Wegen und eigentlich sind alle Hamiltonkreise sehr ansehnlich. Da alle
Kanten vom Grade 2 sind, handelt es sich auch um einen Eulerkreis.
Links ist eine Lösung von Euler. |
Drei Wege
...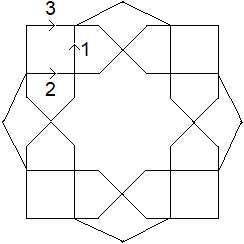 ... ... |
Die Figur ist nach drei Umläufen letztlich durch
eine geschlossene Kurve entstanden.
Man beginnt in 1, passiert 2 und endet in 3. |
... ... ... |
Man erzeugt die Figur am besten durch ein Punktmuster.
Man erhält ein großes Quadrat, indem man in
die Ecken kleine Quadrate setzt und dazwischen in dieser Reihenfolge ein
halbes Quadrat, ein Quadrat und ein halbes Quadrat. Das große Quadrat
erhält noch vier Punkte, indem man die Mittelpunkte des kleinen Quadrats
spiegelt.
Die Punkte werden passend verbunden. |
Die Figur stammt von Volker Sayn.
Kurven, die durch Punkte gesteuert werden. findet man
auf meiner Webseite Kolams und Sona.
Weitere Figuren top
...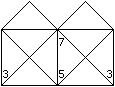 .... .... |
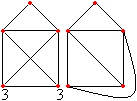
Oben werden zwei Häuser getrennt gezeichnet. Man
kann in der Mitte eine Wand weglassen. Der Spruch lautet dann: "Das
ist das Haus vom Ni-ko-laus, ne-ben-an vom Weih-nachts-mann". |
In dieser Ausführung ist die Figur nicht lösbar.
Es gibt vier Knoten mit ungeradem Grad.
Deshalb ist kein Weg einmal durch alle Kanten möglich.
Lässt man die gemeinsame Wand weg, wird das Doppelhaus
wieder lösbar.
Man stellt fest (das Internet macht
diese Feststellung möglich), dass im englischen Sprachbereich das
Haus des Nikolaus ziemlich unbekannt ist. Man findet es manchmal
als "envelope". Man betrachtet stattdessen Figuren, die Eulerkreise zulassen.
Hier einige Beispiele:

...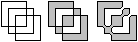 ... ... |
Die Suche nach Eulerkreisen wird leichter, wenn man die
Figuren schwarzweiß färbt.
Das zeigt die Lösung des Drei-Quadrate-Problems
von Lewis Carrol. |
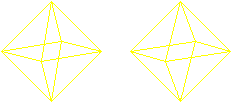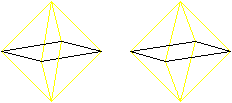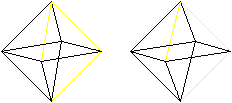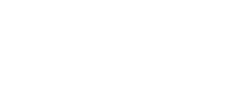
Euler- und Hamiltonwege gibt es auch
bei manchen Körpern.
Als Beispiel kann das Oktaeder dienen, bei dem an einer
Ecke immer vier Kanten zusammentreffen.
Wer den 3D-Blick beherrscht, sieht die Oktaeder auch
dreidimensional.
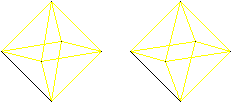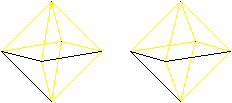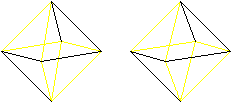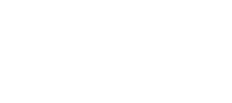
Hamiltonkreis
Beim Hamiltonkreis sollte man an einen Angestellten eines
Paketzustelldienstes denken, der nacheinander seinen Kunden (=Knoten) die
Pakete ausliefert. |
.................. |
Eulerkreis
Beim Eulerkreis bietet sich zur Veranschaulichung ein Briefträger
an, der jeden Tag bestimmte Straßen (=Kanten) abgeht, um die Post
zuzustellen. |
Zugabe: Kuboktaeder
und quadratisches Antiprisma
Figuren aus
einem (geschlossenen) Linienzug top
1. Beispiel: top
.........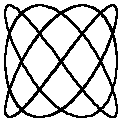 .............. .............. |
In der Mathematik und Physik sind Lissajous-Figuren Beispiele
für berechnete Linien ohne Anfang und Ende.
Mehr Linien dieser Art findet man in meinen Webseiten
"Eilinien" und "Spirograph". |
2.Beispiel:
top
Die Werbung lässt sich diese Spielerei nicht entgehen.
(Danke, Redzep)

|
Er liegt in Bodenheim. |
3.Beispiel:
top
Im Bereich der Kunst wird man fündig.
Da wären der Hund und die Friedenstaube-Bilder von
Picasso, wobei dieser sich durch das Prinzip der geschlossenen Linie nicht
einengen ließ.
Es gibt auch Beispiele von Paul Klee:
Drohender Schneesturm (1927), Kleiner Narr in Trance
(1927),
Altes Fräulein (1931) (entstanden aus einem sich
abwickelnden Faden)
Mit Rücksicht auf das Copyright verzichte ich auf
eine Darstellung.
Drei alte Schreibspiele
top
Häuser
Dieses ist ein Schreibspiel für ältere Kindergartenkinder,
genannt "Häuser".
...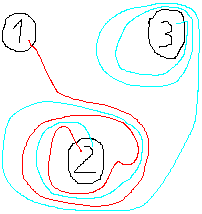 ... ... |
Zu Beginn werden 10 Häuser auf einem Blatt DIN-A4
Papier verteilt. Sie werden als Kreise mit Nummern dargestellt. Die Mitspieler
müssen der Reihe nach die Häuser durch Wege verbinden. Die Wege
dürfen aber nicht die schon gezeichneten Wege berühren oder gar
kreuzen. Für jede Berührung gibt es einen Strafpunkt. Findet
doch eine Berührung statt, so dürfen die nachfolgenden Spieler
die Kreuzungen überqueren und erhalten keine Strafpunkte.
Die nebenstehende Zeichnung zeigt, dass die Spieler schon
etwas älter sind, denn es sind schon Schikanen in Form von Spiralen
eingebaut.
|
Eigentlich sollte wegen des Nachahmungseffekts die folgende
Aussage nicht gemacht werden. Aber es war eben so: Für jeden Strafpunkt
musste man sich ein Haar ausziehen lassen :-(.
Einkaufen
Das Wort/Schreibspiel "Einkaufen" kann Kindergartenkinder
erfreuen.

|
Frau Meier,
zwei Eier, eine Wurst, einen Kamm.
Bitte wickeln Sie alles ein,
mit zwei Henkeln dran zum Anfassen.
Ein paar Stecknadeln,
eine Streichholzschachtel,
einen riesengroßen Kuchen mit Rosinen drin,
einen Besen, einen Schrubber.
Macht zusammen 66. |

|
Milch
holen
Eins habe ich noch, auch von Generation zu Generation
weitergegeben.
... ... ...
|
Ein Mädchen guckt aus dem Fenster, der Milchmann
ist da. Schnell hin und Milch gekauft.
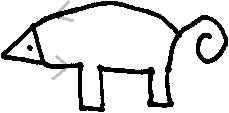
Das Mädchen stolpert und steht wieder auf (1.Bein).
Es läuft weiter (Bauch).
Es stolpert wieder und steht wieder auf (2.Bein).
Es gießt die ganze Milch aus (Schwanz als Spirale)
und läuft nach Haus (Rücken). |
|
Falls man das Tier nicht erkennt, es ist ein Schwein.
Referenzen top
(1) Hermann Schubert: Mathematische Mußestunden,
Berlin 1941
Anmerkung
... ... ... |
Als mir dieses Buch in die Hände fiel, versah ich
den ersten Satz dieser Seite doch lieber mit einem Fragezeichen. (Das
Haus des Nikolaus ist ein uraltes (?) deutsches Zeichenspiel für kleine
Kinder.)
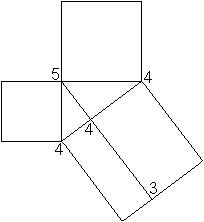
Im Kapitel Eulersche Wanderungen
wird auch ein Figur gezeigt, die wie beim Haus vom Nikolaus keine
Eulerkreise, wohl aber Eulerwege zulässt. Die Figur links ermöglicht
es, den Satz des Pythagoras zu beweisen.
Wäre Schubert das Haus vom
Nikolaus bekannt gewesen, hätte er diese ungewöhnliche Figur
wohl durch das Haus ersetzt.
Wenn ich zurückdenke, ich
lernte das Nikolaushaus in den 1940er / 1950er Jahren als Kind kennen. |
(2) Will Grohmann, Paul Klee,
Handzeichnungen, Köln 1959
(3) Martin Gardner: Mathematisches Labyrinth, Braunschweig/Wiesbaden
1979 [ISBN 3-528-08402-2]
(4) Monika Dewess, Günter Dewess (Hrsg.): Summa
Summarum, Thun / Frankfurt/Main 1986 [ISBN 3-87144-898-2]
(5) Peter Gritzmann, René
Brandenberg: Das Geheimnis des kürzesten Weges, Springer Berlin...,
2002
[ISBN 3-540-42028-2]
Das Buch nenne ich aus zwei Gründen. Es enthält
einen Link auf diese Seite :-). Zum anderen ist es eine gute Einführung
in die
Diskrete Mathematik (speziell Graphentheorie). Bei der Lektüre
des Buches wird klar, dass dieser relativ neue Forschungsbereich
Anwendungen in vielen Bereichen unserer Wirklichkeit hat.
Das
Haus
des Nikolaus im Internet top
Englisch
Behance
One-line-Animal-logos
Eric W. Weisstein (MathWorld)
Eulerian
Cycle
Torsten Sillke
Counting
Eulerian Circuits and Tours
Wikipedia
Eulerian
path,
Seven
Bridges of Königsberg, La
Linea , Space-filling
curve, Glossary
of graph theory
Deutsch
Dirk Brundelius
Das ist das
Haus vom Nikolaus (alle 44 Häuser als "animated Gifs")
Klaus Huneke
Dies
ist das Haus vom Nikolaus, Acryl auf Nessel, Startseite
Lutz Tautenhahn
Nikulus
Wikipedia
Haus
vom Nikolaus,
Eulerkreisproblem,
Hamiltonkreisproblem,
Königsberger
Brückenproblem, La
Linea, Raumfüllende
Kurve
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
1999 ... 2004 Jürgen Köller
top |