|
Was ist ein Ikosidodekaeder?
... ... ...
|
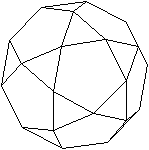
Ein Ikosidodekaeder ist
ein Körper, der von und 20 gleichseitigen Dreiecken und 12 regelmäßigen
Fünfecken gebildet wird.
Neben den 20+12=32 Seitenflächen hat es 60 Kanten
und 30 Ecken. |
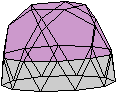
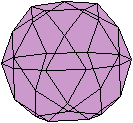
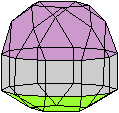
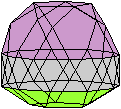
Wer den 3D-Blick beherrscht,
sieht das Ikosidodekaeder räumlich.
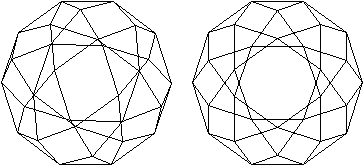
durchsichtig
|
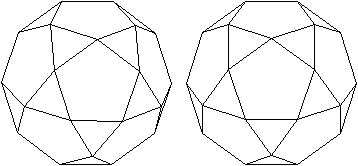
undurchsichtig
|
Entstehung
Das Ikosidodekaeder entsteht aus einem Ikosaeder, wenn
man an den Ecken passend fünfseitige Pyramiden abschneidet. Dazu halbiert
man die Kanten des Ikosaeders.
...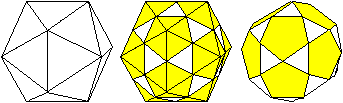 ... ... |
An den Ecken des Ikosaeders entstehen Fünfecke.
Die Dreiecke des Ikosaeders werden auf kleinere Dreiecke
reduziert. |
Einordnung
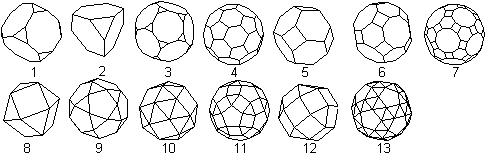 Da beim Ikosidodekaeder (9) an jeder Ecke regelmäßige
Vielecke in gleicher Weise aufeinandertreffen, gehört es zu den 13
archimedischen
Körpern.
Da beim Ikosidodekaeder (9) an jeder Ecke regelmäßige
Vielecke in gleicher Weise aufeinandertreffen, gehört es zu den 13
archimedischen
Körpern.
Beschreibungen top
Umgebungen der Drei- und Fünfecke
....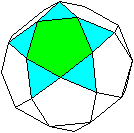 ... ... |
Auf jeder Fünfeckseite liegt ein Dreieck. Es entsteht
ein Stern.
Der gleiche Stern liegt auf der entgegengesetzten Seite.
Die beiden Fünfecke liegen parallel und sind gegeneinander
um 180° gedreht. |
...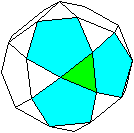 .... .... |
Zu jeder Dreieckseite gehört ein Fünfeck.
Die gleiche dreistrahlige Figur liegt auf der entgegengesetzten
Seite.
Die beiden Dreiecke sind parallel und gegeneinander um
180° gedreht. |
... ... ... |
Jedes Dreieck ist nur von Fünfecken und jedes Fünfeck
nur von Dreiecken umgeben. |
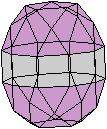
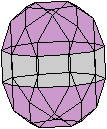
Zehneck
...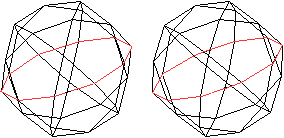 ... ... |
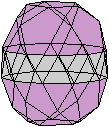
Es gibt Kanten im Ikosidodekaeder, die ein ebenes, regelmäßiges
Zehneck bilden. - Es gibt 6 verschiedene Zehnecke.
Die Ebene durch ein Zehneck ist Symmetrieebene und halbiert
das Ikosidodekaeder. |
Parallelprojektionen
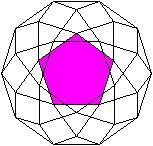
Ein Fünfeck liegt vorne.
|
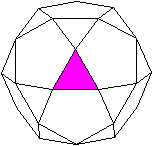
Ein Dreieck liegt vorne.
|
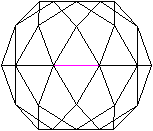
Eine Kante liegt vorne.
|
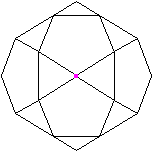
Eine Ecke liegt vorne.
|
Netze
...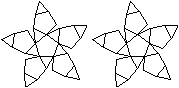 ... ...
|
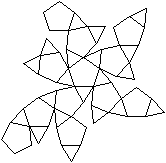
|
Schlegel-Diagramm
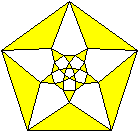
Diagonalen
60 Flächendiagonalen
...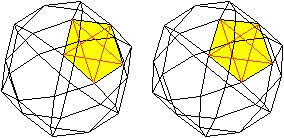 .... .... |
Die Diagonalen der 12 Fünfecke bilden die Flächendiagonalen
des Ikosidodekaeders. Jedes Fünfeck hat 5 Diagonalen.
Das führt zu insgesamt 12*5=60 Flächendiagonalen. |
315
Raumdiagonalen
..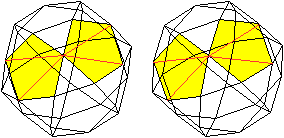 .... .... |
Von jedem der 30 Eckpunkte gehen Verbindungslinien zu
den anderen Eckpunkten aus. Das sind 4 Flächendiagonalen und 4 Kanten,
wie die Zeichnung zeigt. In 30-8=22 Punkten enden dann Raumdiagonalen.
Das führt zu insgesamt (1/2)*30*21=315 Raumdiagonalen
des abgestumpften Ikosaeders. |
Bilanz
Auf meiner Seite Dreieckszahlen
steht: "Verbindet man n Punkte mit allen möglichen geraden Linien,
so ergeben sich 1+2+3+...+(n-1)=(1/2)(n-1)n Strecken."
Für das Ikosidodekaeder bedeutet das, dass es (1/2)*29*30=435
Verbindungslinien gibt.
Das sind die 60 Kanten, 60 Flächendiagonalen und
315 Raumdiagonalen.
Größen top
Das Ikosidodekaeder sei durch die Kantenlänge a
gegeben.
Daraus lassen sich u.a. die weiteren Größen
Radius R der Umkugel, Radius rk der Umkugel, Volumen
V
und Oberfläche O,
Abstand der Dreiecke d3
und Abstand der Fünfecke
d5 berechnen.
Es gilt:
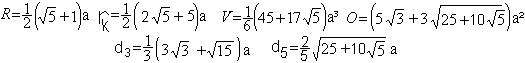
Herleitung der Formeln
Folgende Formeln werden u.a. in diesem Kapitel benutzt.
Ikosaeder: (hier: a' = 2a)
Volumen V' = (5/12)[3+sqrt(5)]a'³
Radius der Inkugel: r' = (1/12)sqrt(3)[3+sqrt(5)]a' |
...
Radius der Umkugel: R' = (1/4)sqrt[10+2sqrt(5)]a'
Abstand gegenüberliegender Kanten
2x' = (1/2)[1+sqrt(5)]a' |
Radius
der Umkugel
Auf meiner Seite Ikosaeder wird ein Würfel betrachtet,
der das Ikosaeder umhüllt. Die Kantenlänge dieses Würfels
ist der Durchmesser der Umkugel.
Es gilt x' = R = (1/2)[sqrt(5)+1]a.
Radius
rk der Kantenkugel
Bei archimedischen Körpern liegen die Kantenmitten
auf einer Kugel, der Kantenkugel.
...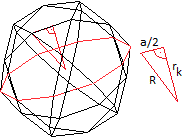 ... ... |
Der Radius rk der Kantenkugel kann über
den Radius R der Umkugel bestimmt werden.
Im rechtwinkligen Dreieck gilt rk² =
R²-[(1/2)a]².
Weiter ist rk² = (1/4)[1+sqrt(5)]²a²-(1/4)a²
= (1/4)[6+2sqrt(5)]a²-(1/4)a² = (1/4)[5+2sqrt(5)]a².
Dann ist rk= (1/2)sqrt[5+2sqrt(5)]a, wzbw. |
Oberfläche
Die Oberfläche setzt sich aus 20 Dreieckflächen
und 12 Fünfeckflächen zusammen.
Es gilt O = 20*[sqrt(3)/4]a²+12*{(1/4)sqrt[25+10*sqrt(5)]}a²
=
...
= {5sqrt(3)+3sqrt(5)sqrt[5+2sqrt(5)]}a².
Abstand
der Fünfecke
...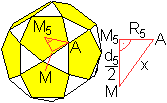 ... ... |
Zur Orientierung: M ist der Mittelpunkt des Ikosaeders
bzw. des Ikosidodekaeders, M5 ist der Mittelpunkt des Fünfecks.
Der dritte Punkt A ist (auch) eine Kantenmitte des Ikosaeders. Das Dreieck
ist rechtwinklig und gestattet es, den halben Abstand der Fünfecke
zu berechnen. Es gilt nach dem Satz des Pythagoras: (d5/2)²
= x'²-R5² |
Also ist (d5/2)²
= x'²-R5² = {(1/2)[1+sqrt(5)]a'}²-{R5 =
(1/10)[sqrt[50+10sqrt(5)]a}² =...
= [1-(2/5)sqrt(5)]a²
Dann ist d5 = (2/5)sqrt[25+10sqrt(5)]a, wzbw..
Volumen
Man erhält das Volumen, wenn man vom Volumen des
erzeugenden Ikosaeders die Volumina der 12 fünfeckigen Pyramiden abzieht.
Es gilt V = V'-12*V5.
Es gilt V = V' = (5/12)[3+sqrt(5)]a'³ = (10/3)[3+sqrt(5)]a³
Die Berechnung von A5 ist mühsam und an
zwei Stellen trickreich.
V5 = (1/3)*A5*(R'-d5/2)
= (1/3)*(1/4)sqrt[25+10sqrt(5)]a²*{(1/4)sqrt[10+2sqrt(5)]a'-(1/5)sqrt[25+10sqrt(5)]a}
= (1/3)*(1/4)sqrt[25+10sqrt(5)]a²*(1/4)sqrt[10+2sqrt(5)]a'-(1/3)*(1/4)sqrt[25+10sqrt(5)]a²*(1/5)sqrt[25+10sqrt(5)]a
V5/a³ = (1/3)(1/4)(1/4)2sqrt[25+10sqrt(5)]sqrt[10+2sqrt(5)]-(1/3)(1/4)(1/5)sqrt[25+10sqrt(5)]sqrt[25+10sqrt(5)]
= (1/24)sqrt{[25+10sqrt(5)][10+2sqrt(5)]}-(1/60)sqrt{[25+10sqrt(5)][25+10sqrt(5)]}
= (1/24)sqrt[350+150sqrt(5)]-(1/60)sqrt[1125+500sqrt(5)]
= (5/24)sqrt[14+6sqrt(5)]-(1/12)sqrt[45+20sqrt(5)]
= [(5/24)sqrt(2)]sqrt[7+3sqrt(5)]-[(1/12)sqrt(5)]sqrt[9+4sqrt(5)]
Derive hilft weiter.
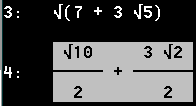
sqrt[7+3sqrt(5)]=(1/2)[sqrt(10)+3sqrt(2)]
|
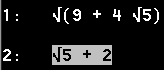
sqrt[9+4sqrt(5)]=2+sqrt(5)
|
V5/a³ = [(5/24)(1/2)sqrt(2)][7+3sqrt(2)]-[(1/12)sqrt(5)][2+sqrt(5)]
= (5/48)[sqrt(20)+6]-[(1/12)[2sqrt(5)+5]
= (1/24)sqrt(5)+5/24 oder V5={(1/24)sqrt(5)+5/24}a³
V = V'-12*V5
= (10/3)[3+sqrt(5)]a³-12*{(1/24)sqrt(5)+5/24}a³
= 10+(10/3)sqrt(5)-(1/2)sqrt(5)-5/2}a³
= [(15/2+(17/6)sqrt(5)]a³
= (1/6)[45+17sqrt(5)]a³
wzbw..
Abstand
der Dreiecke
Dieser Abstand ist gleich dem Durchmesser
des Inkreises des Ikosaeders.
d3 = 2r' = 2*(1/12)sqrt(3)[3+sqrt(5)]a'
= (1/3)[3sqrt(3)+sqrt(15)]a.
Ein
Winkel
Ferner gilt nach (1): Der Winkel zwischen einer Dreieck-
und Fünfeckfläche ist 142°37'.
"Abgestumpftes
Pentagondodekaeder" top
...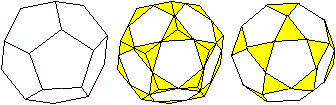 ... ... |
Das Ikosidodekaeder entsteht auch aus einem Pentagondodekaeder,
indem man die Ecken passend abschneidet.
Dazu halbiert man die Kanten des Pentagondodekaeders
und schneidet an den Ecken dreieckige Pyramiden ab. |
> Geht man vom Ikosaeder aus, so kann man es durch dreieckige
Pyramiden zu einem Pentagondodekaeder ergänzen.
> Oben wurde gezeigt, dass man es auch durch Aufsetzen
von Fünfeckpyramiden zu einem Ikosaeder erweitern kann.
Das Ikosidodekaeder ist sozusagen der Kern von Ikosaeder
und Pentagondodekaeder.
Diese Überlegung erklärt den Namen Ikosidodekaeder.
Unter einem abgestumpften
Pentagondodekaeder versteht man offiziell einen anderen Körper.
Er heißt kürzer abgestumpftes
Dodekaeder.
.....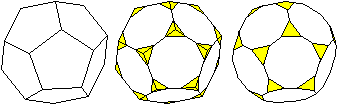 . . |
Zur Herstellung wird jede Kante so aufgeteilt, dass regelmäßige
Zehnecke entstehen. Die entstehenden Dreieckspyramiden werden dann entfernt.
Es entsteht ein Körper aus 20 Dreiecken und 12 Zehnecken. |
Weitere Körper
Abgestumpftes Ikosaeder.
...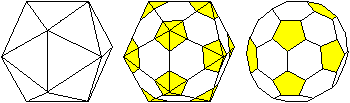 ... ... |
Es gibt einen zweiten archimedischen Körper, der
durch Abschneiden der Ecken aus einem Ikosaeder hervorgeht.
Das ist das abgestumpfte
Ikosaeder. Man erhält es, wenn man nicht so tief wie oben abschneidet.
Die Kante an einer Ecke wird nur um ein Drittel gekürzt. |
Rhombentriakontaeder
...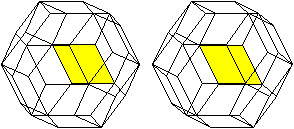 ... ... |
Verbindet man die Mittelpunkte benachbarter Seitenflächen
des Ikosidodekaeders, so entsteht der duale Körper, das Rhombentriakontaeder. |
Fünfecksrotunde
... ... ...
|
...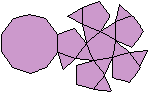 ... ... |
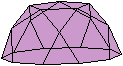
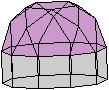
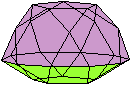
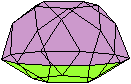
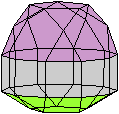
Halbiert man ein Ikosidodekaeder, so entsteht ein Körper,
der nur von regelmäßigen Vielecken gebildet wird, nämlich
von einem Zehneck, 6 Fünfecken und 10 Dreiecken. Das ist die Fünfecksrotunde,
der
Johnson-Körper
J6. |
Die Fünfecksrotunde
ist Bestandteil weiterer Johnson-Körper.
Oktaeder
im Ikosidodekaeder
...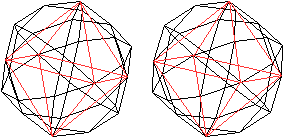 ... ... |
Verbindet man 6 bestimmte Eckpunkte des Ikosidodekaeders,
so entsteht ein Oktaeder. - Es gibt 5 verschiedene Oktaeder.
Alle Oktaeder zusammen bilden das "octahedron 5-compound",
das man sich auf der Webseite Icosidodecahedron von MathWorld (URL
unten) ansehen kann. |
Ein Leuchtstern top
Im November 2006 erwarb ich für einen Euro in einem
Billigladen einen Leuchtstern. Er hat keinen Namen und nur die Angabe "Made
in China". Er veranlasste mich, diese Seite zu machen.
... ... ... |
Der dreidimensionale Stern besteht aus sechs fünfzackigen,
ebenen Sternen, die ineinander verwoben sind.
Sie schließen eine Plastikkugel ein, die für
kurze Zeit in drei Farben blinkt, wenn man den Stern vorher fallen lässt. |
... ... ... |
Ich konnte nicht umhin, ihn
auseinander zu nehmen.
... ... ... |
Auf diesem Foto sind die Sterne isoliert.
So ist die Kugel aus der Mitte freigelegt. |
... ... ... |
Und was hat der Leuchtstern
mit dem Ikosidodekaeder zu tun?

|
Verbindet man die Spitzen des Sterns, so entsteht ein
Ikosidodekaeder. |
.. .... .... |
Schaut man senkrecht auf ein Fünfeck des Ikosidodekaeders,
so liegt - wie schon oben angemerkt - hinten ein zweites Fünfeck parallel
und um 180° gedreht.
Dazwischen liegt in der Mittelebene ein regelmäßiges
Zehneck, das von Kanten des Ikosidodekaeders gebildet wird. |
...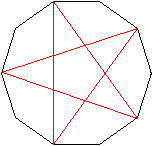 ... ... |
Verbindet man in diesem Zehneck jeden vierten Eckpunkt,
so entstehen die fünfzackigen Sterne, aus denen der Leuchtstern aufgebaut
ist.
Es gibt sechs Sterne und somit sechs Schnittebenen, die
den Körper halbieren. |
Ikosidodekaeder
im Internet
top
Deutsch
H. B. Meyer (Polyeder aus Flechtstreifen)
Ikosidodekaeder
Wikipedia
Ikosidodekaeder,
Archimedischer
Körper, Rhombentriakontaeder
Englisch
Eric W.Weisstein (MathWorld)
Icosidodecahedron,
IcosidodecahedralGraph,
Archimedean
Solid
Geneviève Tulloue ( Figures Animées pour
la Physique )
Polyhedra
(Applets)
G. Korthals Altes
Paper
model Icosidodecahedron
H. B. Meyer (Polyeder aus Flechtstreifen)
Icosidodecahedron
Poly
A program
for downloading ("Poly is a shareware program for exploring and constructing
polyhedra")
Die meisten Zeichnungen auf dieser Seite entstanden
mit Hilfe dieses Programms.
Wikipedia
Icosidodecahedron,
Icosahedron,
Archimedean
solid, Rhombentriakontaeder
Französisch
Robert FERRÉOL (mathcurve)
ICOSIDODÉCAÈDRE
Referenzen top
(1) H.Martyn Cundy and A.P.Rollett: Mathematical Models,
Oxford 1961 (Seite 108)
Feedback: Emailadresse
auf meiner Hauptseite
URL meiner Homepage:
https://www.mathematische-basteleien.de/
© 2007,
überarbeitet 2013, Jürgen Köller
top |


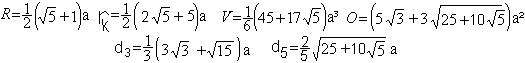
 ...
...

 ...
... ...
... ....
.... ...
... ...
...



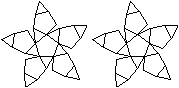 ...
...
 ....
.... ....
....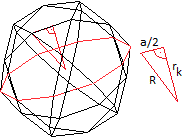 ...
... ...
...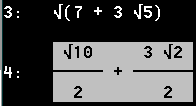
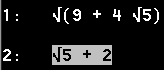
 ...
... .
. ...
... ...
... ...
... ...
...
 ...
... ...
... ...
... ...
... ...
...
 ...
...