Allgemeines Viereck
Inhalt dieser Webseite
Was ist das allgemeine Viereck?
Bezeichnungen
Besondere Vierecke
Wie viele Stücke braucht ein Viereck?
Satz von der Winkelsumme im Viereck
Beziehung zwischen Seiten und Diagonalen
Flächeninhalt eines Vierecks
Rationales Viereck		 Satz von Varignon
Satz von van Aubel
Sehnenenviereck durch Winkelhalbierende
Acht-Punkte-Kreis
Vollständiges Viereck
Parkettierung
Allgemeines Viereck im Internet
.
Zur Hauptseite    "Mathematische Basteleien"

Was ist das allgemeine Viereck?
...... Das allgemeine Viereck entsteht, wenn man vier Punkte A, B, C, D, von denen drei nicht auf einer Geraden liegen, miteinander durch Strecken verbindet. 

"Allgemein" soll heißen, dass das Viereck keine besonderen Eigenschaften hat und dass sich somit Aussagen auf beliebige Vierecke beziehen.

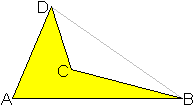...... Die vier Punkte können auch so liegen, dass der vierte Punkt innerhalb des Dreiecks aus drei Punkten liegt. Dann entsteht ein konkaves Viereck.
...... Legt man für die vier Punkte oben eine andere Reihenfolge fest, so entsteht ein überschlagenes Viereck.

Ich beschränke mich auf dieser Seite auf das erste, konvexe Viereck.

Bezeichnungen    top
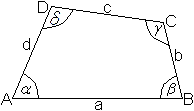...... Man bezeichnet üblicherweise aus praktischen Gründen die Eckpunkte eines Vierecks mit A, B, C, D, die Seiten mit a, b, c, d und die Innenwinkel mit alpha, beta, gamma, delta.

> Zum Punkt A gehört der Winkel alpha. 
> Der Punkt A ist ein Endpunkt der Seite a.
> Die Eckpunkte A, B, C, D und die Seiten a, b, c, d sind entgegengesetzt dem Uhrzeigersinn angeordnet. 
> Der Punkt A liegt möglichst unten links.
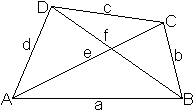...... Die Verbindungsstrecken gegenüberliegender Punkte im Viereck heißen Diagonalen e und f.

Besondere Vierecke   top
Die folgenden neun Vierecke haben besondere Eigenschaften, die in den Namen zum Ausdruck kommen. 

1

2

3

4

5

6

7

8

9

1 Trapez
2 Drachenviereck
3 Parallelogramm		 4 Rechteck
5 Raute
6 Quadrat		 7 Sehnenviereck
8 Tangentenviereck
9 Doppelquadrat
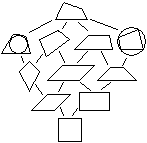...... Übersichten über die Beziehungen zwischen den Vierecken findet man auf meiner Webseite Hierarchie der Vierecke. 

Wie viele Stücke braucht ein Viereck?     top
...... Ein allgemeines Dreieck wird durch drei passende Stücke festgelegt. 

Es stellt sich die Frage, wie viele der acht Stücke a,b,c,d, alpha, beta, gamma. delta das Viereck festlegen. 

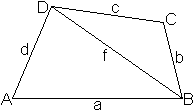...... Dazu zerlegt man das Viereck durch eine Diagonale in zwei Teildreiecke.
Zur Festlegung des Dreiecks ABD benötigt man drei Stücke, zum Beispiel die Seiten. 
Der vierte Punkt C liegt nur dann eindeutig fest, wenn zwei Stücke hinzukommen, zum Beispiel die Seiten b und c. Man braucht auch allgemein fünf Stücke zur Festlegung eines Vierecks. 
Das können Seiten, Diagonalen oder Winkel sein.
Konstruktionen und Berechnungen zum allgemeinen Viereck werden i.a. auf Dreiecke zurückgeführt.

Satz von der Winkelsumme im Viereck    top
... Es gilt der Satz:

Die Summe der Innenwinkel eines Vierecks beträgt 360°. .............................................

Formel: alpha+beta+gamma+delta=360°

Beweis
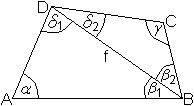...... Die Diagonale f zerlegt das Dreieck in die beiden Teildreiecke ABD und DBC. 
Die Innenwinkel delta und beta werden so in delta1+delta2 bzw. beta1+beta2 zerlegt.
Nach dem Satz von den Innenwinkeln im Dreieck gilt alpha+beta1+delta1=180° und delta2+beta2+gamma=180°. Daraus folgt alpha+beta1+delta1+delta2+beta2+gamma=360° oder alpha+beta+gamma+delta=360°, wzbw.

Beziehung zwischen Seiten und Diagonalen     top
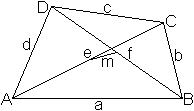...... Zwischen den Seiten a, b, c, d des Vierecks, seinen Diagonalen e, f und der Verbindungslinie m der Mittelpunkte der Diagonalen herrscht die Beziehung
a²+b²+c²+d² = e²+f²+4m².

Offenbar ist diese Formel eine Verallgemeinerung der Parallelogrammgleichung a²+b²+c²+d² = e²+f². 
Dieser Sonderfall wird auf meiner Seite Parallelogramm bewiesen.

Flächeninhalt eines Vierecks    top
Flächeninhalt aus Seiten und Winkeln
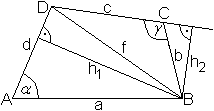Es gilt A=(1/2)[ad*sin(alpha)+cb*sin(gamma)].

Die Diagonale teilt das Viereck in zwei Teildreiecke auf. Es gilt 
A=(1/2)dh1+(1/2)ch2=(1/2)da*sin(alpha)+(1/2)cb*sin(180°-gamma)
   =(1/2)[ad*sin(alpha)+cb*sin(gamma)], wzbw.

Entsprechend gilt A=(1/2)[ab*sin(beta)+cd*sin(delta)].
Formel von Bretschneider
Die Seiten und eine Winkelsumme sind gegeben.
...
A=sqrt[(s-a)(s-b)(s-c)(s-d)-abcds*cos²(phi)]

mit s=(1/2)(a+b+c+d) und phi=(1/2)(alpha+gamma) oder phi=(1/2)(beta+delta) 
Diese Formel wird auf der englischen Wikpedia-Seite unter Bretschneider's formula (URL unten) bewiesen.
Flächeninhalt aus Diagonalen
Die Diagonalen und der Winkel zwischen ihnen sind gegeben.
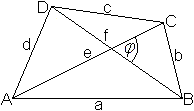... A=(1/2)ef*sin(phi)........................................................................
Beweis
Die Formeln ADreieck==(1/2)ac*sin(beta) und sin(180°-phi)=sin(phi) werden vorausgesetzt.
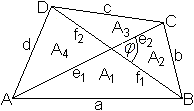Die Diagonalen zerlegen das Viereck in vier Teildreiecke. Es gilt
A=A1+A2+A3+A4
A=(1/2)e1f1sin(180°-phi)+(1/2)e2f1sin(phi)+(1/2)e2f2sin(180°-phi)+(1/2)e1f2sin(phi)
A=(1/2)f1(e1+e2)sin(phi)+(1/2)f2(e1+e2)sin(phi)
A=(1/2)ef*sin(epsilon), wzbw.
Viereck im Koordinatensystem
Sind die Eckpunkte des Vierecks durch Koordinaten in einem kartesischen Koordinatensystem gegeben, kann man den Flächeninhalt aus ihnen berechnen.
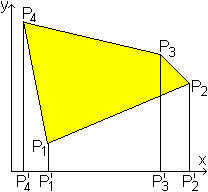...... Ein beliebiges Viereck sei im kartesischen Koordinatensystem durch die Punkte 
P1(x1|y1), P2(x2|y2), P3(x3|y3) und P4(x4|y4) gegeben.
 

Dann ist der Flächeninhalt des Vierecks A=(1/2)|[(x3-x1)(y4-y2) +(x4-x2)(y1-y3)]|.
 
Beweis
Nach der Trapezmethode gilt
A=|A(P4'P3'P3P4)+A(P3'P2'P2P3)-A(P4'P1'P1P4)-A(P1'P2'P2P1)|
=(1/2|(y3+y4)(x3-x4)+(1/2(y3+y2)(x2-x3)-(1/2(y4+y1)(x1-x4)-(1/2(y1+y2)(x2-x1)|
=...
=(1/2)|(x3-x1)(y4-y2)+(x4-x2)(y1-y3)|, wzbw.

Rationales Viereck   top
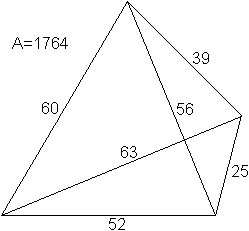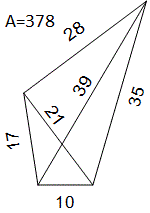
...... Ein rationales Viereck ist ein Viereck mit ganzahligen Seiten und Diagonalen. 
Außerdem ist auch der Flächeninhalt ganzzahlig.

Nach MathWorld (URL unten) ist das linke Viereck das einfachste.

Satz von Varignon   top
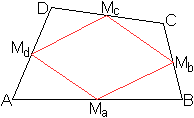...... Verbindet man die Mittelpunkte der Seiten eines beliebigen Vierecks miteinander, so entsteht ein Parallelogramm.

Der Satz heißt Satz von Varignon bzw. Varignon's Theorem.

Beweis
Dieser Beweis benutzt die Vektorrechnung. (Vektoren werden hier mit fetten, kleinen Buchstaben geschrieben.)
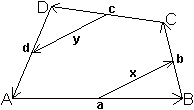...... Es gilt x=(1/2)a+(1/2)b und y=(1/2)c+(1/2)d.
Aus a+b+c+d=0 folgt (1/2)a+(1/2)b+(1/2)c+(1/2)d=0 oder x+y=0 oder x=-y.
Das aber heißt, dass die Vektoren x und y kollinear (parallel) und dem Betrage nach gleich sind. Ein Viereck, das gleich lange und parallele Gegenseiten hat, ist ein Parallelogramm.

Satz von van Aubel    top
...... Gegeben sei ein beliebiges Dreieck. 

Errichtet man über die Seiten gleichseitige Dreiecke und verbindet deren Schwerpunkte, so entsteht wieder ein gleichseitiges Dreieck. 

Dieser Satz ist als Satz des Napoleon in die Literatur eingegangen.

Van Aubels Satz ist eine Übertragung vom Dreieck auf das Viereck.
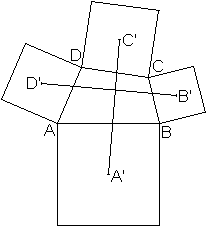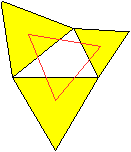
...... Gegeben sei ein beliebiges Viereck. 

Errichtet man über die Seiten Quadrate, dann sind die Verbindungslinien der Mittelpunkte gegenüberliegender Quadrate gleich lang. Außerdem stehen diese Strecken aufeinander senkrecht.

Dieser Satz wird z.B. auf der Webseite van Aubel's Theorem von Antonio Gutierrez bewiesen.

Sehnenviereck durch Winkelhalbierende    top
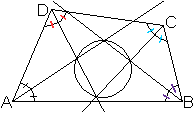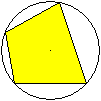
...... Die Winkelhalbierenden eines konvexen Vierecks schneiden sich in vier Punkten. 

Sie bilden ein Sehnenviereck.

Acht-Punkte-Kreistop
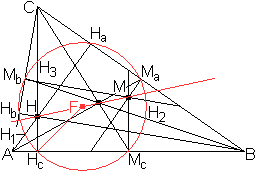...... Beim allgemeinen Dreieck gibt es den Neun-Punkte- oder Feuerbachkreis.

Dem entspricht beim allgemeinen Viereck der Acht-Punkte-Kreis.

Acht-Punkte-Kreis
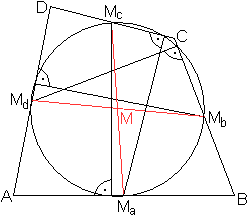...... In einem Viereck legt man auf den Seiten eines allgemeinen Vierecks acht Punkte fest, nämlich die Mittelpunkte der Seiten und die Fußpunkte der Lote, die man von den Mittelpunkten auf die Gegenseiten fällt.

Es gibt einen Kreis, der durch die acht Punkte geht und dessen Mittelpunkt der Schnittpunkt der (roten) Verbindungslinien gegenüberliegender Seitenmitten ist.
 

Vollständiges Viereck top
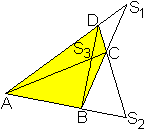...... Neben den vier Eckpunkten gibt es im vollständigen Viereck drei weitere charakteristische Punkte, die aus den Eckpunkten entstehen. Das sind der Schnittpunkt der Diagonalen und die beiden Schnittpunkte, die man erhält, wenn man die Gegenseiten verlängert.

Diese sieben Punkte bilden das vollständige Viereck, das in der Projektiven Geometrie ein Rolle spielt. 

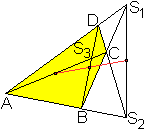...... Im vollständigen Viereck liegt die gaußsche Gerade.

Das ist die Gerade durch die Mittelpunkte der beiden Diagonalen. 
Das Besondere ist, dass auch der Mittelpunkt der Strecke S1S2 auf ihr liegt.
 

Parkettierungtop
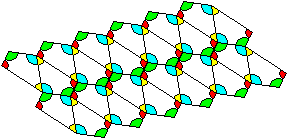...... Man kann mit Vierecken die Ebene parkettieren.

Mehr findet man auf meiner Seite Parkettierung mit Vielecken.

Auf der Webseite Theorem of Complete Quadrilateral (URL unten) von A.Bogomolny kann man mit einem Applet spielen.

Allgemeines Viereck im Internet      top

Deutsch

Eckard Specht   (math4U)
Ungleichungen in Vierecken,  Allgemeines Viereck

Wikipedia
Viereck,  Ungleichungen in Vierecken,  Fano-Axiom, Satz von Varignon


Englisch

Antonio Gutierrez
List of GoGeometry Problems (Solved and Unsolved) - Index
Eight-Point Circle Theorem,  van Aubel's Theorem,  Generalizing Van Aubel' Theorems,  Newton/Gauss line

A. Bogomolny  (Cut The Knot!)
Theorem of Complete Quadrilateral,  The Complete Quadrilateral,  Simple Quadrilaterals Tessellate the Plane

Eric W. Weisstein (MathWorld)
Quadrilateral, van Aubel's Theorem,  Complete Quadrilateral, Rational Quadrilateral, Varignon's Theorem, 
Eight-Point Circle Theorem, Bretschneiders Formula

MathsIsFun.com
Interactive Quadrilaterals

Wikipedia
Quadrilateral, Van Aubel's theorem,  Complete quadrilateral,  Varignon's theorem,  Bretschneider's formula

Feedback: Emailadresse auf meiner Hauptseite

URL meiner Homepage:
http://www.mathematische-basteleien.de/

©  2010 Jürgen Köller

top