Parallelogramm
Inhalt dieser Seite
Was ist ein Parallelogramm? 
Sätze
Formeln
Dreieck und Parallelogramm
Viereck und Parallelogramm		 Gemischtes
Parallelogramme um uns
Parallelogramm im Internet
Referenzen
.
Zur Hauptseite    "Mathematische Basteleien"

Was ist ein Parallelogramm? 
...... Ein Parallelogramm ist - dem Wort folgend - ein Viereck, dessen Gegenseiten parallel sind. 

...... Auch das Rechteck bzw. das Quadrat und die Raute sind Parallelogramme. 
Sie haben zusätzliche Eigenschaften und sind so Sonderfälle des Parallelogramms. 

Sätze      top
Satz 1

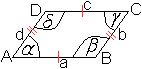Ein Viereck ist genau dann ein Parallelogramm, wenn die Gegenseiten gleich lang sind. 
Beweis:
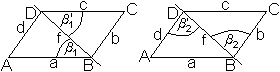...... Zeichnet man die Diagonale f ein, so wird das Parallelogramm in zwei Dreiecke zerlegt. Nach dem Kongruenzsatz sss sind sie kongruent. Damit sind die Winkel beta1 und beta1' gleich groß. Sie sind aber auch Wechselwinkel zu den Geraden AB und CD mit der Schnittgeraden DB. Nach der Umkehrung des Satzes von den Wechselwinkeln an Parallelen gilt AB||CD. 
Die rechte Zeichnung stellt sicher, dass auch BC||AD gilt.
Damit sind die Gegenseiten parallel und das Viereck ist ein Parallelogramm, wzbw..
Wegen des Zusatzes "genau" in Satz 1 gilt auch die Umkehrung. Deshalb hat der Beweis noch einen zweiten Teil.
Voraussetzung ist jetzt, dass die Gegenseiten parallel sind.
...... An der gleichen Zeichnung kann man ablesen, dass die eingezeichneten Winkel nach dem Satz von den Wechselwinkeln an Parallelen gleich sind. Nach dem Kongruenzsatz wsw sind die Dreiecke kongruent. (s steht für die Diagonale f.)
Dann folgt, dass einander zugeordnete Dreieckseiten gleich groß sind: a=c und b=d, wzbw..
Anmerkung
In der Formelsprache heißt der Satz  a||c /\ b||d <=> a=c /\ b=d.
Die Aussagen a||c /\ b||d  und  a=c /\ b=d sind gleichwertig oder äquivalent. 
Man kann das Parallelogramm folglich auch so definieren.
"Ein Viereck ist genau dann ein Parallelogramm, wenn es gleich lange Gegenseiten hat." 
Es gibt weitere äquivalente Aussagen zum Parallelogramm.
Satz 2: 
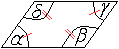Ein Viereck ist genau dann ein Parallelogramm, wenn die Gegenwinkel gleich groß sind. 
Satz 3: 
Ein Viereck ist genau dann ein Parallelogramm, wenn ein Paar Gegenseiten gleich groß und parallel sind. 
Satz 4: 
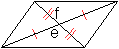Ein Viereck ist genau dann ein Parallelogramm, wenn sich die Diagonalen halbieren. 

Formeln     top
Grundformeln
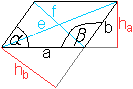...... Größen des Parallelogramms sind die Seiten a und b, die Innenwinkel alpha und beta, die Diagonalen e und f, die Höhen ha und hb und der Flächeninhalt A.

Im Allgemeinen ist ein Parallelogramm durch den Winkel alpha und die Seiten a und b gegeben.
Daraus lassen sich die anderen Größen berechnen.

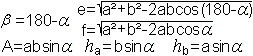
Zu den Herleitungen
Beta:
Entgegengesetzte Winkel an Parallelen ergänzen sich zu 180°.
e und f:
Die Diagonalen teilen das Parallelogramm in zwei kongruente Dreiecke. Auf sie wird der Kosinussatz angewandt.
ha und hb:
Die Formeln ergeben sich aus der Definitionsgleichung "sin (alpha)=Gegenkathete durch Hypotenuse".
A: 
Nach dem Kongruenzsatz Ssw sind die gelben Dreicke kongruent. So gilt A=haa oder A=ab*sin(alpha).
Parallelogrammgleichung
Sie lautet e²+f²=2(a²+b²)
Herleitung
e²+f²=[a²+b²-2ab*cos(180°-alpha)]+[a²+b²-2ab*cos(alpha)] = a²+b²+2ab*[-cos(alpha)]+a²+b²-2ab*cos(alpha)=2(a²-b²), wzbw..
Rechteck und Parallelogramm
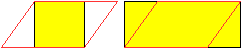...... In Analogie zu Um- und Inkreisen gibt es Rechtecke, die man um und in ein Parallelogramm legen kann. 
Flächenberechnungen
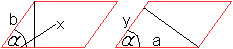... Für die Hilfsgrößen x und y gilt x=b*cos(alpha), y=a*cos(alpha)

Für das "Außenrechteck" gilt Au=(a+x)ha=[a+b*cos(alpha)]ha, für das "Innenrechteck" Ai=(a-x)ha= [a-b*cos(alpha)]ha.

Analoge Formeln ergeben sich über die zweite Höhe hb.

Au=[b+a*cos(alpha)]hb und Ai=[b-a*cos(alpha)]hb

Dreieck und Parallelogramm    top
Dreiecksspiegelung
Das Parallelogramm kann auch aus einem Dreieck hervorgehen, indem man dieses an einer Seitenmitte spiegelt. 
...... Dieser abbildungstheoretische Zugang ermöglicht es, die Eigenschaften der Punktspiegelung  in einfacher Weise auf das Parallelogramm zu übertragen. 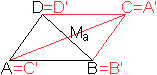Parallele und gleiche Gegenseiten, gleiche Gegenwinkel und die Halbierung der Diagonalen sind einsichtig.

Somit kann man auch Sätze aus der Dreieckslehre auf Parallelogramme übertragen, zum Beispiel die vier Kongruenzsätze. Ein Parallelogramm wird wie das Dreieck durch drei passende Größen festgelegt.
Größtes Parallelogramm im Dreieck
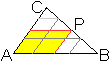...... Gibt man einen Punkt P auf einer Seite (hier BC=a) eines Dreiecks vor und zeichnet durch ihn die Parallelen zu den anderen Seiten, entsteht ein Parallelogramm. Die Frage ist, wo der Punkt P liegen muss, damit das zugehörige Parallelogramm einen möglichst großen Flächeninhalt hat. 
Lösung
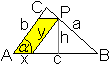...... Das Dreieck ABC sei durch seine Seiten a, b und c gegeben. 
Das Parallelogramm habe die Seiten x und y und die Höhe h. Dann gilt A=xh.
Nach dem zweiten Strahlensatz ist (c-x):c=y:b oder y=(b/c)(c-x). Weiter ist h=y*sin(alpha).
Für den Flächeninhalt heißt das A=xh=xy*sin(alpha)=x(b/c)(c-x)*sin(alpha)=(b/c)sin(alpha)(cx-x²)
Der Term cx-x² nimmt seinen größten Wert für x=c/2 an. Dann ist y=b/2 und folglich ist P der Halbierungspunkt der Seite a.
Ergebnis: Das Parallelogramm wird am größten, wenn der Punkt P die Seite a halbiert.
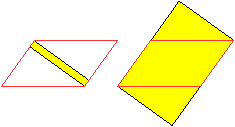
Parallelogramm durch die Seitenhalbierenden
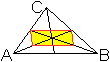...... Die Seitenhalbierenden im Dreieck teilen sich im Verhältnis 2:1. 
Dadurch ist es möglich, wie links ein Parallelogramm in das Dreieck einzupassen.
Parallelogramm mit gleichseitigen Dreiecken
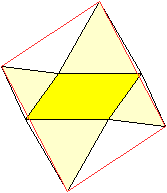...... Errichtet man auf den Seiten eines Parallelogramms vier gleichseitige Dreiecke, so bilden ihre freien Eckpunkte ein Parallelogramm.
Quelle mit Beweis: Alexander Bogomolny unter Equilateral Triangles On Sides of a Parallelogram (URL unten)

Viereck und Parallelogramm    top
Mittenviereck im Parallelogramm (Satz von Varignon)
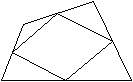...... Satz:
Verbindet man in einem beliebigen Viereck die Mittelpunkte der Seiten, so ergibt sich ein Parallelogramm.

1.Beweis 
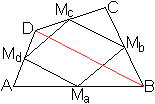...... Man zeichnet die Diagonale BD ein.
Im Dreieck ABD gilt die Proportion AMa:AB=AMd:AD (=1:2).
Nach der Umkehrung des ersten Strahlensatzes sind dann MaMd und BD parallel.
Entsprechend zeigt man MbMc||BD.
Damit sind zwei Gegenseiten des Mittenvierecks parallel.
Auf dem gleichen Wege zeigt man, dass auch die anderen Gegenseiten  MaMb und McMd parallel sind.
Damit ist das Mittenviereck ein Parallelogramm, wzbw..
2. Beweis mit den Methoden der Vektorrechnung
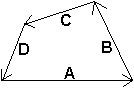...... Man führt die Seitenvektoren A, B, C und D ein.

Es gilt A+B+C+D=0.
......
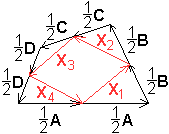 Die vier Seitenvektoren werden durch die Summe der halb so langen Vektoren ersetzt.
Dann gilt X1= (1/2)A+(1/2)B, X2=(1/2)B+(1/2)C, X3=(1/2)C+(1/2)D, X4=(1/2)D+(1/2)A
Weiter ist X1+X3=(1/2)A+(1/2)B+(1/2)C+(1/2)D=(1/2)(A+B+C+D)=0 
und X2+X4=(1/2)B+(1/2)C+(1/2)D+(1/2)A=(1/2)(A+B+C+D)=0 
Aus X1+X3=0 folgt X1=-X3 und aus X2+X4 folgt X2=-X4.
Damit sind die Seiten des Mittenvierecks paarweise parallel. Das Mittenviereck ist ein Parallelogramm, wzbw..
Ein zweites Parallelogramm im Viereck
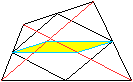...... Verbindet man die Mittelpunkte der Diagonalen mit den Mittelpunkten zweier Gegenseiten des allgemeinen Vierecks, so entsteht ein Parallelogramm.
Quellen mit Beweisen: Matroid (URL unten), MATH4U unter W.2(URL unten)
Parallelogramm über die Mittelpunkte der Seiten
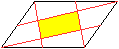...... Verbindet man jeweils den Mittelpunkt einer Seite eines Parallelogramms mit einem Eckpunkt in gleicher Weise, so entsteht im Inneren ein Parallelogramm.
Mehr darüber bei Antonio Gutierrez unter Parallelogram with Midpoints (URL unten)
Wittenbauers Parallelogramm
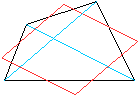...... Teilt man die Seiten eines beliebigen Vierecks in drei gleiche Teile und zeichnet durch die Teilpunkte wie links Geraden, so entsteht ein Parallelogramm.

Je zwei Gegenseiten des Parallelogramms sind parallel zu den Diagonalen.
Quelle mit Beweis: Alexander Bogomolny unter Wittenbauer's Parallelogram (URL unten)
Parallelogramm und fünf Quadrate
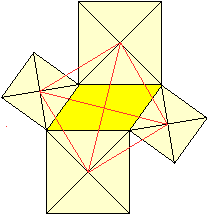...... Errichtet man auf den Seiten eines Parallelogramms vier Quadrate, so bilden ihre Mittelpunkte auch ein Quadrat.
Quellen mit Beweis: 
>MATH4U unter M.7 (URL unten)
>Antonio Gutierrez unter Parallelogram with Squares Theorem (URL unten)
Verallgemeinerung
Geht man nicht von einem Parallelogramm, sondern von einem beliebigen Viereck aus, so wird aus dem Quadrat ein Rechteck.
Quelle mit Beweis:  Antonio Gutierrez unter Van Aubel's Theorem: Quadrilateral with Squares (URL unten)

Gemischtes     top
Parallelogramm der Kräfte
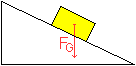...... Legt man einen Klotz auf eine geneigte Ebene, so wirkt auf ihn die Gewichtskraft FG. Nur bei hinreichend großer Reibung bleibt er liegen. Ist sie nicht vorhanden, so rutscht der Klotz die Ebene hinunter. Das muss eine Kraft bewirken.

...... Die folgende Kräftebetrachtung bringt Klarheit: Die Gewichtskraft wird durch den Hangabtrieb FH und die Normal(en)kraft FN ersetzt. Das gewährleistet der Satz vom Parallelogramm der Kräfte. 
Im Falle der geneigten Ebene ist das Parallelogramm ein Rechteck.
Ergänzungsparallelogramm
...... Gegeben sind ein Parallelogramm und eine Strecke a'.
Gesucht ist die Konstruktion eines zweiten, winkel- und flächengleichen Parallelogramms mit der Seite a'. 
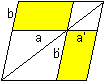...... Die Lösung besteht darin, die Ausgangsfigur zu einem Ergänzungsparallelogramm (links) zu erweitern.
Teilverhältnis im Parallelogramm
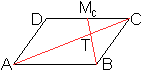...... Verbindet man in einem Parallelogramm den Eckpunkt mit dem Mittelpunkt einer gegenüberliegenden Seite wie links, so teilt diese Transversale die Diagonale im Verhältnis 2:1.
Beweis:
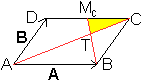Man führt zwei Grundvektoren ein und bildet im Dreieck TCMc eine Vektorkette.


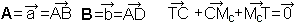
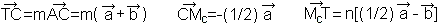m und n sind die Streckenverhältnisse auf der Diagonalen und der (anderen) Transversalen.
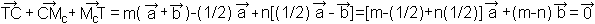Da die Grundvektoren A und B linear unabhängig sind, folgt sowohl  m-(1/2)+(1/2)n=0 als auch m-n=0. 
Dann ist m=n=1/3. 
Ergebnis: Die Transversale BMc und die Diagonale AC teilen sich im Verhältnis 2:1.
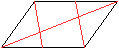...... Zeichnet man eine zweite Transversale wie links ein, so wird die Diagonale in drei gleiche Teile geteilt.
Parallelogramm und Vektoren
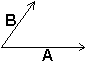...... Es gibt zwei Verknüpfungen von Vektoren, die durch Parallelogramme veranschaulicht werden.
Summe
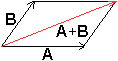...... Man erhält den Summenvektor über die Diagonale des von den Vektoren aufgespannten Parallelogramms.
Vektorprodukt
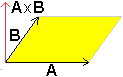...... Man erhält das Vektorprodukt, indem man nach der Rechten-Hand-Regel bei geöffneter Hand den Vektor A auf kürzesten Wege in Richtung Vektor B bewegt und und dem Produkt die Richtung des Daumens gibt. Die Länge des Vektors AxB wird durch den Flächeninhalt des von den Vektoren gebildeten Parallelogramms bestimmt.
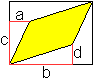...... Ist ein Parallelogramm in nebenstehender Figur durch die Strecken a,b,c und d gegeben, so ist sein Flächeninhalt A=ad-bc.

Diese Formel geht auf das Vektorprodukt zurück. Die Vektoren sind durch Koordinaten gegeben.
Parallelepiped (Spat)
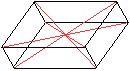...... Sechs geeignete Parallelogramme bilden einen Körper, das Parallelepiped.
Es ist ein "verformter" Quader.
Wie bei diesem schneiden sich die Raumdiagonalen in einem Punkt.
Zwei optische Täuschungen
Die beiden Parallelogramme sind gleich, auch wenn es nicht so aussieht.
...... Die Diagonalen in den nebeneinander liegenden Parallelogrammen erscheinen  verschieden lang. Das ist aber eine optische Täuschung. 

Parallelogramme um uns top

Treppenaufgang in Bad Salzuflen/Schötmar in der Begastraße 25

Unser Nähkasten, ein Erbstück

Zum Nähkasten ist zu noch bemerken, dass er eine Anwendung des Satzes ist, dass ein Viereck genau dann ein Parallelogramm bleibt, wenn die Seitenlängen erhalten bleiben. Das wird durch den Bau gesichert. - Die Laden bleiben horizontal, weil die unterste Lade fest steht.
Ein Merkmal der Weserrenaissance sind schräge Fenster an Türmen von Burgen und Schlössern.
Hinter den Turmfenstern liegen die Treppen.
Dieses sind zum Beispiel zwei schräge Fenster des Schlosses Brake in Lemgo.

Parallelogramme an anderen Stellen meiner Homepage

Hierarchie der Vierecke

Achsen- und punktsymmetrische Figuren


Papierformat A4

Wie viele Parallelogramme?
Figuren in einer Figur

Parallelogramm im Internet  top
Man findet mit einer Suchmaschine mehr Seiten zum Thema Parallelogramm mit Hilfe verschiedener Schreibweisen. 
So liefert Google am 15.November 2008:
78.700 Seiten (Parallelogramm)
27 (Parrallelogramm), 575 (Paralelogramm), 86 (Parallellogramm)
30 (Parralelogramm), 3 (Parrallellogramm), 1820 (Paralellogramm)
16 Parralellogramm
56 (Parallogramm -Parallogram), 9 (Parallegramm -Parallegram), 0 (Parallagramm -Parallagram),
36 (Parallelgramm -Parallelgram)

588.000 Seiten (Parallelogram)
2620 (Parrallelogram), 34100 (Paralelogram),   21.900 (Parallellogram)
1260 (Parralelogram),  43 (Parrallellogram),   5330 (Paralellogram)
287 (Parralellogram)
2610 (Parallogram), 750(Parallegram),  92 (Parallagram), 1850 (Parallelgram)

Jetzt kommt noch diese Seite dazu ;-).


Deutsch

Eckard Specht
MATH4U.DE
M.7 Parallelogramm mit Quadraten (mit Beweis)
W.2 Ein zweites Parallelogramm im Viereck (mit Beweis)

Matroid
Vergessene Sätze am Dreieck / 
2 Der Satz von Varignon  3 Der Satz von Pappus

Wikipedia
Parallelogramm, Parallelogrammgleichung, Parallelepiped, Wittenbauer's Parallelogram,  Varignon-Parallelogramm, Kräfteparallelogramm, Pantograf,  Antiparallelogramm


Englisch

Antonio Gutierrez
> Parallelogram with Squares Theorem (Thébault's Theorem),  Van Aubel's Theorem: Quadrilateral with Squares, Generalizing Van Aubel' Theorems
> Parallelogram with Midpoints , Varignon's Theorem
> Similar Triangles, Incenters, Parallelogram, Similar Triangles, Circumcircles, Parallelogram
> Areas: Problem161, Problem162, Problem164, Problem165, Problem166, Problem167, Problem168, Problem169

Alexander Bogomolny (cut-the-knot)
Varignon's parallelogramm,  Wittenbauer's Parallelogram,  Octagon In Parallelogram, 
Equilateral Triangles On Sides of a Parallelogram

Eric W. Weisstein (MathWorld)
Parallelogram, Varignon Parallelogram,  Lozenge, Parallelogram Illusion

Kimberly Burrell, Brad Simmons, Doug Westmoreland
Pappus Areas

PHILIPPE R. RICHARD (UNIVERSIT ´E DE MONTR´EAL)
Proof Without Words: Equal Areas in a Partition of a Parallelogram  (.pdf-file)

Project IES
Pantograph (Applet),  Horizontal Machine,  Problem about parallelogram, 

Vernon Morris 
Parallelograms

Wikipedia
Parallelogram, Parallelogram of force,  Gnomon (figure), Parallelepiped, Sander illusion, Pantograph,  Antiparallelogram

Referenzen    top
Lothar Kusch, Mathematik für Schule und Beruf, Teil 2, Essen 1971 [ISBN 3 7736 2582 0] Seite 70ff.

Feedback: Emailadresse auf meiner Hauptseite

URL meiner Homepage:
http://www.mathematische-basteleien.de/

©  2008 Jürgen Köller

top