|
Was ist Tetragon?
Tetragon ist ein Legespiel des Geometrie-Ingenieurs Urs
B. Roth aus der Schweiz von 1984.
Es besteht aus acht ähnlichen Vierecken aus Plexiglas,
aus denen man ein Quadrat und viele weitere Figuren legen kann.
Beschreibung
der Vierecke
Beim Tetragon-Spiel sind die Figuren acht ähnliche
Vierecke.
... |
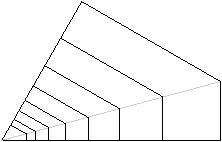Das sind die Figuren noch einmal in perspektivischer
Lage. |
... ... |
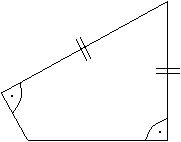Jedes Viereck hat zwei gegenüber liegende rechte
Winkel und zwei nebeneinander liegende gleiche Seiten. |
... ... |
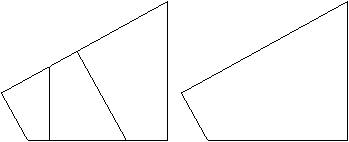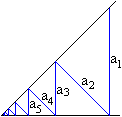
Das Besondere ist, dass immer drei aufeinander folgende
Vierecke eine zu den Ausgangsvierecken ähnliche Figur bilden. |
Etwas Mathematik top
Bestimmung des Streckfaktors k
... .......... |
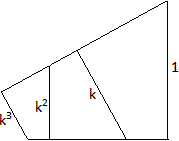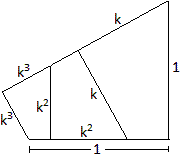
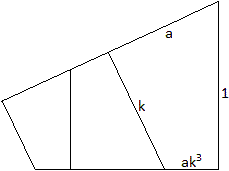
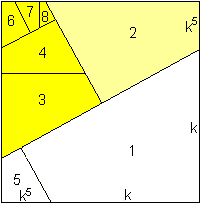
Man betrachtet drei aufeinander folgende Vierecke, die
zusammen ein neues Viereck bilden.
Da sie ähnlich sind, stehen entsprechende Seiten
in einem festen Verhältnis, nämlich k.
Bezeichnet man zwei gegenüber liegende Seiten des
größten Vierecks mit 1 und k, so haben die übrigen Seiten
die Längen k und k² bzw. k² und k³. |
... ... |
Zwei nebeneinander liegende Seiten sind gleich............................................................................... |
... ... |
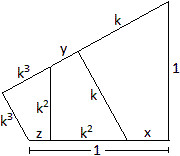Für die drei noch fehlenden Seiten gelten folgende
Proportionen.
x:k = k3:1 oder x = k4,
y:k2 = k3:1 oder y = k5,
z:k3 = k3:1 oder z=k6.............................................................................................................. |
... .. |
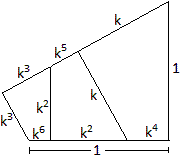Damit sind alle Seiten durch Terme mit k ausgedrückt.
In der Zeichnung kann man als Grundseite ablesen: k6
+
k4 + k2 = 1.
Diese Gleichung gestattet es, den
Streckfaktor k zu berechnen................................................ |
Die Gleichung k6
+
k4 + k2 = 1 führt mit x=k2 zur kubischen
Gleichung x3+x2+x-1=0.
Die reelle Lösung lautet:
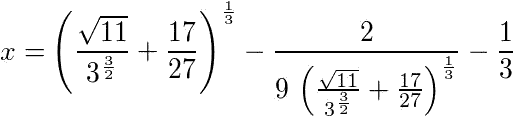Das führt zur Dezimalzahl x=0,54368901 an.
Dann ist der Streckfaktor k=sqrt(x)=0,73735270 oder sinnvoll
gerundet k=0,7374.
Anmerkung:
Bei OEIS (URL unten) hat die kubische Gleichung x3+x2+x-1=0
die Lösung
x = (1/3)*(-1-2/(17+3*sqrt(33))^(1/3)+(17+3*sqrt(33))^(1/3))
oder angenähert x=0.54368901269207636157... .
Die Konstante r ist der reziproke Wert der sogenannten
Tribonacci-Konstanten.
Bestimmung
eines Innenwinkels eines Vierecks
.... .. |
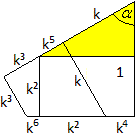Es gilt tan(alpha)=(k2+k4)/(1-k2)
oder einfacher tan(alpha) = 1/k2.
Setzt man nämlich (k2+k4)/(1-k2)=
1/k2, so ist (k2+k4)k2 =1-k2
oder k6
+ k4 + k2 = 1.
Aus tan(alpha)=1/k² folgt tan(alpha) = 1,8393 oder
alpha=61,5°.
Der stumpfe Innenwinkel hat dann eine Größe
von 118,5°.
|
Bestimmung
der Flächeninhalte der Vierecke
... ... |
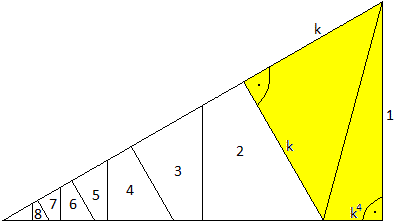Das größte Viereck besteht aus zwei rechtwinkligen
Dreiecken und hat einen Flächeninhalt von
A1 = (1/2)k2+(1/2)k4 =
(1/2)k2(1+k2).
Da die Vierecke ähnlich sind, stehen die Flächeninhalte
im Verhältnis k².
Dann ist A2=(1/2)k2(1+k2)*k2
=(1/2)k4(1+k2)
und allgemein An=(1/2)k2n(1+k2)
(n=1, 2, 3,..., 8). |
Aufbau
eines Quadrates
Legen von Figuren top
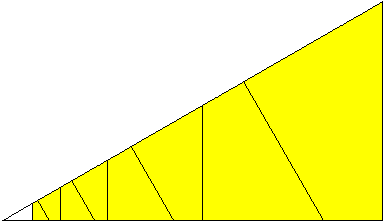
Die Vierecke sind Glieder einer geometrischen
Folge bzw. Reihe und lassen sich deshalb zu einer Zickzacklinie oder
zu einer Spirale anordnen.
Es gelingt, aus ihnen neben
dem Quadrat gängige Vierecke wie das Trapez, das Rechteck und das
Parallelogramm zu legen.
Wie bei Tangram hat auch
das Legen abstrakter Figuren ihren Reiz. Die Figuren sind nach dem Schwierigkeitsgrad
geordnet.
Aus der Sammlung von Urs B. Roth
Verwandte Legespiele
top
Tangram
Tangram besteht aus sieben Figuren, die aus kongruenten
gleichschenklig-rechtwinkligen Dreiecken aufgebaut sind.
Aufgabe ist es, aus allen sieben Figuren neue Figuren zu
legen. Die Grundfigur ist das Quadrat rechts.
Trigon
... ... |
Trigon ist eine Legespiel von Wilhelm Kienzle von 1951
und ist bei Naef 1958 erschienen.
Es enthält neun ähnliche, rechtwinklige Dreiecke,
die eine geometrische Folge bilden.
Zusammen bilden sie ein Quadrat mit einem quadratischen
Loch, in dem ein Würfel liegt.
Ein Dreieck setzt sich aus zwei kleineren der Folge zusammen.
Die Seitenlängen des Dreiecks sind [ 1, sqrt(t),
t ] mit t = [sqrt(5)+1]/2.
Die entscheidende Konstante ist also die des goldenen
Schnitts.
Mehr findet man im Buch "Kurt Naef: der Spielzeugmacher"
bei Google Books (URL unten). |
Verschiedenes
top
Zwei bemerkenswerte Strecken
1
... .... |
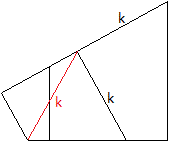Betrachtet man drei aufeinander folgende Vierecke, so
gibt es in der Figur eine weitere Strecke der Länge k. |
Beweis
Für die folgende Rechnung werden die Formeln k6+k4+k2
=
1 (s.o.) und k8+1 = 2k2 bereitgestellt.
Die zweite Formel ergibt sich aus der Diagonale im rechten
Viereck. Es gilt 2x der Satz des Pythagoras.
... |
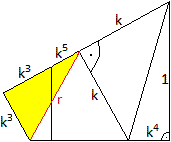Nach dem Satz des Pythagoras gilt r2=k6+(k3+k5)2.
r2=k2[k4+(k2+k4)2]
= k2[k4+k4+2k6+k8]
=k2[2k4+2k6+2k2-1]
=k2[2(k4+k6+k2)-1]
=k2 wzbw. |
2
.... .... |
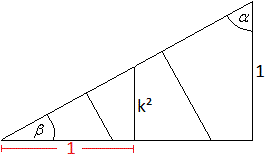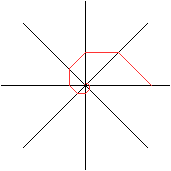
Als Glieder einer geometrischen Reihe liegen die Vierecke
im Winkelraum des Winkels beta=90°-alpha.
Die Lage von drei aufeinander folgenden Vierecken kann
wegen tan(alpha)=1/k² durch die gekennzeichnete Einheitsstrecke angegeben
werden. |
Beweise
des Satzes von Pythagoras
.... .... |
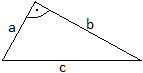Der Satz des Pythagoras lautet bekanntlich: Im rechtwinkligen
Dreieck gilt c² = a²+b².
Es ist möglich, mit Hilfe des Vierecks des Tetragons
mit einem beliebigem, spitzem Innenwinkel Beweise zu finden. |
1.Beweis
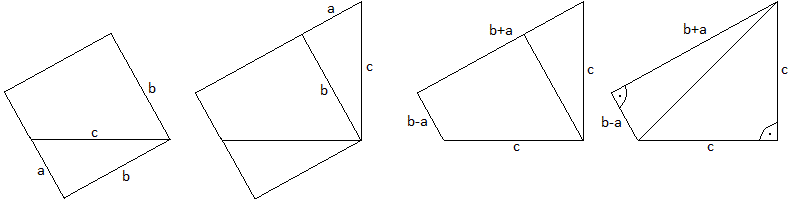
> Man ergänzt das rechtwinklige
Dreieck zu einem Quadrat mit der Seitenlänge b und dem Flächeninhalt
b².
> Das Dreieck unten schneidet man
ab und setzt es oben rechts an.
> Es entsteht ein Viereck mit den
Seiten c, c , a-b und a+b.
> Das Viereck hat den Flächeninhalt
von (1/2)c²+(1/2)(a+b)(a-b).
Da das Ausgangsquadrat und das Viereck den gleichen Flächeninhalt
haben, gilt
b² = (1/2)c²+(1/2)(b+a)(b-a)
<=> 2b² = c²+(b²-a²)
<=> c²=a²+b²,
wzbw.
Quelle:
http://www.cut-the-knot.org/pythagoras/index.shtml#27, Proof #51
2.Beweis
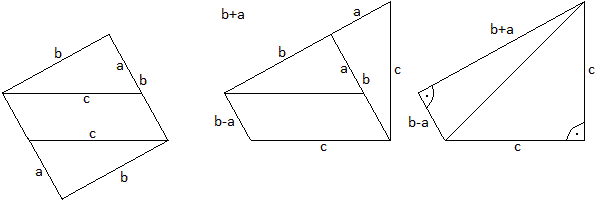> Man ergänzt wieder das rechtwinklige
Dreieck zu einem Quadrat mit der Seitenlänge b und dem Flächeninhalt
b².
> Zusätzlich zeichnet man das Dreieck noch einmal
in die obere rechte Ecke ein.
> Das Dreieck unten schneidet man
ab und setzt es oben rechts an.
> Es entsteht ein Viereck mit den
Seiten c, c , a-b und a+b.
> Für den Flächeninhalt
des Vierecks gilt A=(b-a)b+2*(1/2)ab =b².
Mit A=(1/2)c²+(1/2)(a+b)(a-b)
gilt wieder c²=a²+b², wzbw.
Quelle:
http://www.cut-the-knot.org/pythagoras/index.shtml#27, Proof #51
3.Beweis
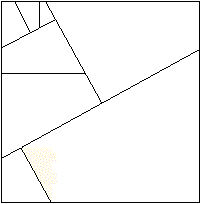
Der Zerlegungsbeweis geht auf Perigal (1873) zurück.
.... .... |
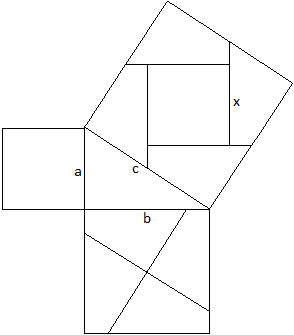In diesem Beweis werden vier kongruente Vierecke des
Tetragons (allerdings mit mit beliebigen Innenwinkel) zu einem Quadrat
b² angeordnet und dann neu zu einem größeren Quadrat c²+x²,
so dass in der Mitte ein quadratisches Loch entsteht. Es muss x=a bewiesen
werden.
Dann gilt dann nämlich c² = a²+b². |
Vorbereitung
.... .... |
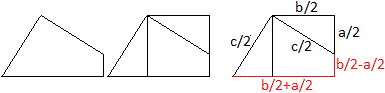Vorweg sei festgestellt, dass man das Viereck in ein
flächengleiches Quadrat verwandeln kann, indem man ein Dreieck rechts
abschneidet und es oben ansetzt.
Bezeichnet man die Seiten des Dreiecks mit c/2, b/2 und
a/2, so hat das Viereck die Seiten c/2, c/2, b/2-a/2 und b/2+a/2. |
.... .... |
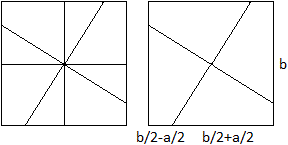So ist leicht einzusehen, dass vier Vierecke ein Quadrat
bilden.
Die Quadratseiten sind b. Sie werden aufgeteilt in die
Teilstrecken b/2-a/2 und b/2+a/2. |
| ........ |
Man liest ab:
x=[b/2+a/2]-[b/2-a/2] = a, wzbw. |
In den bisherigen Beweisen
wird dasselbe Prinzip verfolgt: Aus dem Quadrat wird das Viereck mit Seiten
aus einer Differenz und einer Summe.
4.Beweis
Der Zerlegungsbeweis ist bekannt unter dem Namen "Stuhl
der Braut".
.... .... |
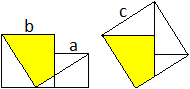Man gibt zwei nebeneinander liegende Quadrate mit den
Seitenlängen a und b vor. Man teilt die Figur so auf,
dass sie zu einem neuen Quadrat der Länge c zusammengesetzt
werden können. Es gilt a²+b²=c².
Der Satz passt zu dieser Webseite, weil ein Viereck mit
gegenüberliegenden rechten Winkeln auftritt. |
Beweis
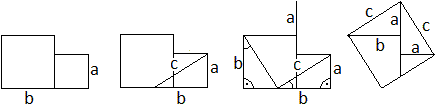> Man geht von den beiden Quadraten aus.
> Man zeichnet die Seite c ein, so dass das rechtwinklige
Dreieck mit den Seiten a, b und c entsteht.
> Man verbindet einen Eckpunkt mit dem oberen, linken
Eckpunkt des rechten Quadrats. Es entsteht ein rechtwinkliges Dreieck.
> Nach dem Satz WWS sind die Dreiecke kongruent. Man
zeichnet oben die Strecke a ein.
> Man schneidet die Dreiecke unten ab und setzt sie oben
an. Es ist ein Quadrat der Seitenlänge c entstanden.
Es gilt a²+b²=c².
Reptiles
und Irreptiles
... ... |
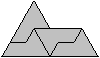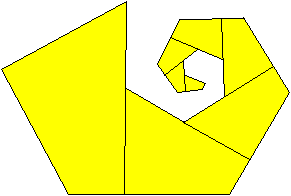
Reptiles sind Figuren, die man
aus kleineren kongruenten Kopien von ihnen legen kann.
(Das Wort sollte man nicht übersetzen,
weil sonst das Wortspiel Rep(eat)-Tiles verloren geht.) |
| ...... |
Sind die Teilfiguren nur ähnlich
und bilden eine zu ihnen ähnliche Figur, so spricht man von Irreptiles.
Insofern bilden drei aufeinander
folgende Vierecke des Tetragons Irreptiles. |
... ... |
Eine Sammlung von Irreptiles findet
man bei Erich Friedmann von der Stetson University in DeLand, Fla. (URL
unten).
Darunter ist auch die links stehende
Konstruktion von Erich Friedmann.
Die Vierecke sind allgemeiner. Sie
haben zwar auch zwei gegenüber liegende rechte Winkel, aber keine
gleiche Seiten. Beim Viereck des Tetragons ist a=k. |
Nachbemerkung top
Dieses ist eine Neubearbeitung meiner Webseite Tetragon.
Die alte Version vom April 2013 hatte das Schlusswort "Ruedi Lang wies
mich auf das Legespiel hin. Er hat sich intensiv mit ihm beschäftigt
und sandte mir umfangreiches Informationsmaterial zu, das ich für
diese Seite verwende."
Im Januar 2014 fand der Entwickler des Spiels,
Herr Urs B. Roth, diese Seite und stellte mir weiteres Material zur Verfügung,
mit dem ich sie jetzt mit seinem Einverständnis ergänze.
Urs B. Roth
Atelier für Konkrete Kunst
Räffelstr.25 8045 Zürich
Tel/Fax 044 450 45 00
ubroth (at) bluewin.ch
In der Kulturzeitschrift "du" Nr. 10 vom
Oktober 1988 äußert er sich zu Tetragon:
"Auf der Suche nach Formen, die sich in zu sich selbst
ähnlichen Formen zerlegen lassen, stieß ich auf ein spezielles
Viereck mit zwei rechten Winkeln. Eine geometrische Folge solcher Vierecke
hat die Eigenschaft, dass jedes Element aus der Summe der drei vorangegangenen
Elemente gebildet werden kann. Durch Zufall entdeckte ich, dass sich 8
aufeinanderfolgende Teile dieser Folge zu einem Quadrat zusammensetzen
lassen.
Aus diesen 8 Teilen lassen sich aber auch eine Vielzahl
anderer Figuren (Rechteck, Parallelogramm, Trapez, etc.) bilden. Dies inspirierte
mich zu einem Legespiel in Anlehnung an das berühmte chinesische Tangram."
(Auszug)
Torsten Sillke und Urs B. Roth veranlassten
mich, meine ursprüngliche Rechnung zu vereinfachen.
Statt eines Innenwinkels sollte man besser den Streckfaktor
in den Mittelpunkt einer Berechnung stellen.
Verwandte
Legespiele im Internet top
Deutsch
Google Books
Kurt
Naef: der Spielzeugmacher
Naef
Hersteller
von Spielobjekte
Wikipedia
Abgeschrägtes
Hexaeder
Englisch
Alexander Bogomolny
Pythagorean
Theorem
Anzeige bei WorthPoint
Naef
Trigon Wooden Puzzle Swiss Made
Liste von Erich Friedman
Reptiles
- Problem of the Month (October 2002)
OEIS
A192918 The
real root r of the cubic equation r^3 + r^2 + r - 1 = 0 is the reciprocal
of the tribonacci constant A058265.
A058265 Decimal
expansion of the tribonacci constant, the solution to x^3=x^2+x+1.
Wikipedia
Generalizations
of Fibonacci numbers, Snub
cube, Rauzy fractal
Feedback: Emailadresse
auf meiner Hauptseite
URL meiner Homepage:
http://www.mathematische-basteleien.de/
© 2013,
überarbeitet 2014, Jürgen Köller
top
|
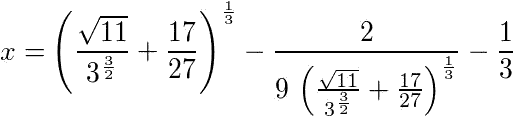
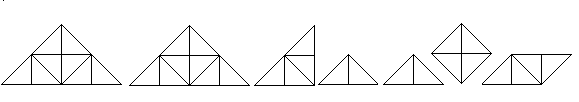
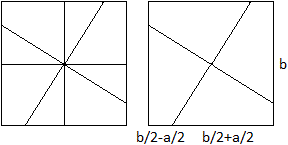