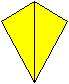
|
Was ist ein Drachenviereck?
... ...
|
Definition:
Ein Viereck heißt Drachenviereck oder Deltoid,
wenn es symmetrisch zu einer Diagonalen ist. |
Der folgende Satz ist auf
die andere Diagonale bezogen.
... ...
|
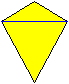
Zwei gleichschenklige Dreiecke mit gleicher Grundseite
bilden ein Drachenviereck, wenn man sie Grundseite an Grundseite zusammenfügt. |
... ... |
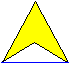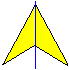
Sind beide gleichschenkligen Dreiecke gleich gerichtet,
so entsteht ein konkaves Drachenviereck. Symmetrieachse eines Drachenvierecks
ist immer die Gerade, die die Diagonale enthält. |
... ... |
... ...
|
Sind beide Diagonalen Symmetrieachsen, so entsteht ein
besonderes Drachenviereck, die Raute.
Auch das Quadrat ist eine Raute und damit ein Drachenviereck. |
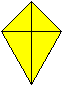
Eigenschaften top
|
>Je zwei nebeneinanderliegende Seiten sind gleich.
>Ein Paar gegenüberliegender Winkel ist gleich.
>Das andere Winkelpaar wird durch eine Diagonale halbiert.
>Die Diagonalen stehen senkrecht aufeinander.
>Eine Diagonale wird durch die andere halbiert. |
Diese Aussagen können nach den Gesetzen der Achsenspiegelung
oder mit Hilfe der Kongruenzsätze bewiesen werden.
Größen top
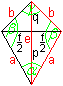
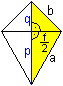
Das Drachenviereck hat die Seiten a und b,
die Innenwinkel
alpha,
beta
und
gamma, die Diagonalen
e
und f, den Umfang
U und den Flächeninhalt
A.
Die Diagonale e hat die Abschnitte
p und q.
... ... |
Angenommen, die Längen a, b und e seien gegeben.
Dann lassen sich die übrigen Größen daraus
errechnen. |
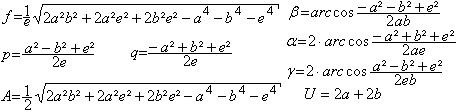
Zur Herleitung der Formeln
Diagonalenabschnitt p
... ...
|
Nach dem Satz des Pythagoras gilt b²=q²+(f/2)²
und a²=p²+(f/2)². Dann ist b²-q²=a²-p².
Mit q=e-p ergibt sich p=(a²-b²+e²)/(2e).
q=e-p=(-a²+b²+e²)/(2e) |
Diagonale f
(f/2)²=a²-p²=(2a²b²+2a²e²+2b²e²-a4
-b4-e4)/(4e²).
Daraus folgt f=(1/e)sqrt(2a²b²+2a²e²+2b²e²-a4
-b4-e4).
Innenwinkel
beta
Nach dem Kosinussatz ist e²=a²+b²-2ab
cos(beta). Daraus folgt beta=arc cos [a²+b²-e²)/(2ab)].
Innenwinkel
alpha und gamma
Es gilt cos(alpha/2)=p/a=[(-a²+b²+e²)/(2ae)].
Daraus folgt alpha=2 arc cos[(-a²+b²+e²)/(2ae)].
Es gilt cos(gamma/2)=q/b=[(a²-b²+e²)/(2be)].
Daraus folgt gamma=2 arc cos[(a²-b²+e²)/(2be)].
Flächeninhalt
A
A=e(f/2)=sqrt(2a²b²+2a²e²+2b²e²-a4
-b4-e4)/2
Umfang
U
U=2a+2b
Inkreis
... ... |
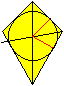Der Mittelpunkt des Inkreises liegt auf der Symmetrieachse
und auf der Winkelhalbierenden des Winkels beta.
Fällt man vom Mittelpunkt aus das Lot auf eine Seite,
erhält man den Radius.
Formel? |
Umkreis
Nur für einen Sonderfall des Drachenvierecks gibt
es einen Umkreis.
... ... |
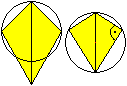Der Mittelpunkt eines Umkreises muss auf der Symmetrieachse
und auf den Mittelsenkrechten der Seiten a und b liegen.
Diese drei Bedingungen sind nur erfüllt, wenn das
halbe Drachenviereck ein rechtwinkliges Dreieck ist. |
Diagonalen top
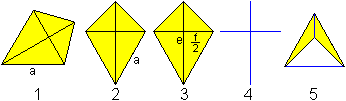1 Im Allgemeinen legt man ein Viereck so, dass der
Eckpunkt A unten links und die Seite a horizontal liegt.
2 Stattdessen wird das Drachenviereck so gedreht,
dass eine Diagonale vertikal steht. Dann liegt die andere Diagonale horizontal.
3 Sind die Diagonalen des Drachenvierecks bekannt,
so lässt sich der Flächeninhalt besonders einfach bestimmen.
Es gilt A=ef/2.
4 Die Diagonalen bilden ein lateinisches Kreuz.
Das Drachenviereck entsteht, wenn man die Endpunkte verbindet.
5 Zur Definition des Drachenvierecks ist das Kreuz
nicht brauchbar, denn beim konkaven Drachenviereck entsteht kein Kreuz.
Schwerpunkt top
Man sieht ein, dass der Schnittpunkt der Diagonalen nicht
als "Mittelpunkt" eines Drachenvierecks angesehen werden kann.
... ... |
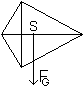Man erwartet, dass er auf der Symmetrieachse liegt, dass
er aber zum größeren gleichschenkligen Dreieck hin verschoben
ist, etwa so, wie links dargestellt.
Dieser Punkt heißt Schwerpunkt. |
Unter einem Schwerpunkt versteht man allgemein den Punkt
eines Körpers, in dem man sich die Masse vereinigt vorstellen und
in dem die Schwerkraft angreifen kann.
Man muss sich also vorstellen, dass das Drachenviereck
eine Masse hat und zum Beispiel als Pappscheibe vorliegt.
Legt man die Scheibe mit dem Schwerpunkt auf eine Nadelspitze,
so bleibt sie waagerecht liegen.
Hängt man die Scheibe in einem Punkt außerhalb
der Symmetrieachse auf, so liegt der Schwerpunkt unterhalb des Aufhängepunktes.
Auf diesen Wegen kann man den Schwerpunkt experimentell bestimmen.
Man findet den Schwerpunkt
zeichnerisch, indem man zunächst mit Hilfe der Seitenhalbierenden
die Schwerpunkte der gleichschenkligen Dreiecke bestimmt, aus denen das
Drachenviereck besteht.
... ... |
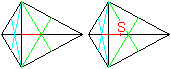Dann trägt man die rote Strecke (p/3) des rechten
Dreiecks vom Schwerpunkt des linken Dreiecks aus auf der Diagonalen ab.
Der freie Endpunkt der roten Strecke ist der Schwerpunkt. Die Begründung
liefert die folgende Rechnung. |
... ... |
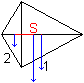Die Drehmomente der Dreiecke, bezogen auf den Schwerpunkt,
heben sich auf und sind dem Betrage nach gleich: F1s1=F2s2
. |
Die Gewichtskräfte sind proportional den Flächeninhalten:
F1=kA'=kfp/2, F2=kfq/2. Dann ist s1:s2
=q:p.
Andererseits ist p/3+q/3=s1+s2.
Das sind zwei Gleichungen mit zwei Variablen, die zu
s1=q/3 und s2 =p/3 führen.
Ergebnis: Der Schwerpunkt hat die Entfernungen q/3+2p/3
und p/3+2q/3 von zwei Eckpunkten.
Polydrachen top
... ... |
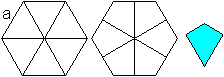Man kann ein regelmäßiges Sechseck so aufteilen,
dass sechs Drachenvierecke entstehen.
Ein Viereck hat die Winkel 90°, 60°, 90°
und 120°
und die Seiten sqrt(3)a/2, sqrt(3)a/2, a/2 und a/2. |
Diese Stücke kann man wie die Pentominos als Spielsteine
benutzen.
Es gibt zum Beispiel zehn Figuren, die man aus vier Drachenvierecken
bilden kann.
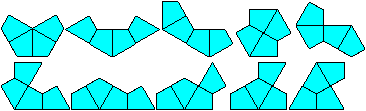
Wie bei Pentominos kann man aus den zehn Tetradrachen
(Tetrakites) neue Figuren bilden.
Verallgemeinerung
Der Polydrachen hat unten einen Winkel von alpha = 60°
und oben einen Winkel von gamma = 120°. Es stellt sich die Frage, wie
man sich einen Überblick verschafft über die Drachenvierecke
mit gamma = 2*alpha. Dazu könnte man so vorgehen.
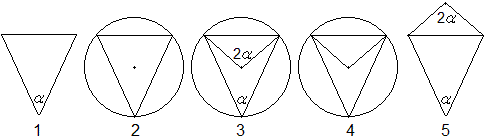1 Gib ein beliebiges gleichschenkliges Dreieck vor.
2 Zeichne den Umkreis.
3 Verbinde den Mittelpunkt mit den Endpunktes der Seite
oben.
Es ist eine Figur entstanden, für die der Satz:
"Der Mittelpunktswinkel ist doppelt so groß wie der zugehörige
Umfangswinkel." gilt.
4 Spiegele das neue Dreieck an der Seite oben.
5 Das ist ein beliebiges Drachenviereck mit gamma = 2*alpha.
Das Problem stammt von Axel
Hahn.
Penrose-Kacheln
top
... ... |
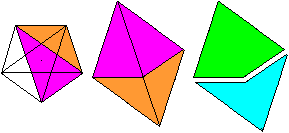In einem regelmäßigen Fünfeck bilden
Seiten und Diagonalen gleichschenklige Dreiecke. Aus ihnen bildet man durch
Achsenspiegelung zwei Drachenvierecke, die zusammen eine Raute bilden.
Sie gehören zu den Penrose-Kacheln. |
... ... |
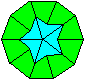Mit diesen Figuren kann man nicht nur ein regelmäßiges
Zehneck bilden, sondern auch die Ebene unbegrenzt auslegen. Das Besondere
ist, dass mit diesen Kacheln die Parkettierung nichtperiodisch sein kann. |
Eine andere Penrose-Parkettierung mit zwei Sorten von Rauten
findet man auf meiner Seite Rauten.
Drachenviereck
im Internet top
Deutsch
Wikipedia
Drachenviereck,
(Flug-)Drachen
Englisch
Brendan Owen (Andrew Clarke's PolyPages)
Polykites
Eric E. Weisstein (MathWorld)
Kite,
Polykite
John Page (Math Open Reference)
Kite
Wikipedia
Kite
(geometry)
Feedback: Emailadresse
auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2004 Jürgen Köller
top |
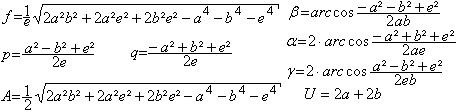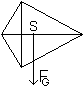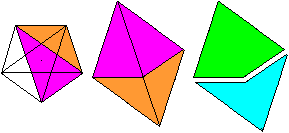