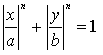|
Was ist eine Raute?
Eine Raute (oder ein Rhombus) ist ein Viereck mit gleich langen Seiten.
|
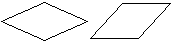Das nebenstehende Viereck in zwei Ansichten hat diese Eigenschaft und
ist eine Raute. |
... ...
|
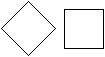
Auch ein Quadrat hat gleich lange Seiten
und ist deshalb eine Raute. Es ist ein Sonderfall der Raute. |
Die Raute wiederum ist ein Sonderfall des Parallelogramms und des Drachenvierecks.
Eigenschaften der Raute top
Gegenwinkel
... ...
|
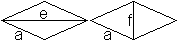Zeichnet man in die Raute die Diagonale e oder die Diagonale f ein,
so entstehen nach dem Kongruenzsatz SSS zwei kongruente gleichschenklige
Dreiecke. Die Winkel an der Spitze sind gleich.
Es gilt also für die Raute: Gegenüberliegende Innenwinkel
sind gleich. |
Gegenseiten
... ... |
Die Gegenseiten sind parallel.
Begründung: Da die Diagonale zwei kongruente Dreiecke erzeugt,
sind Stufenwinkel gleich. Folglich sind nach der Umkehrung des Satzes von
den Stufenwinkeln die Gegenseiten parallel. |
Diagonalen
... ...
|
Zeichnet man in die Raute beide Diagonalen ein, so kann jeweils eine
halbe Diagonale als Höhe in einem gleichschenkligen Dreieck
gesehen werden.
Daraus folgt: Die Diagonalen halbieren sich und stehen aufeinander
senkrecht.
Die Diagonalen halbieren die Innenwinkel. |
Die Raute ist achsensymmetrisch bzgl. der Diagonalen und punktsymmetrisch
bzgl. des Mittelpunktes.
Es gilt auch die Umkehrung: Stehen in einem
Viereck die Diagonalen aufeinander senkrecht und halbieren sich, so ist
das Viereck eine Raute.
Zum Beweis dieser Richtung: Die Diagonalen bilden nach dem Kongruenzsatz
SWS vier kongruente Dreiecke. Die Hypotenusen sind gleich.
Mittenviereck 1
... ...
|
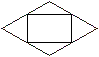Verbindet man die Seitenmitten einer Raute, entsteht ein Rechteck.
Zum Beweis: Man zeichnet nacheinander die Diagonalen ein. Die Seiten
des Mittenvierecks sind Mittelparallelen im jeweiligen Dreieck. |
Mittenvierecke 2
... ... |
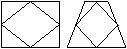Verbindet man die Seitenmitten eines Rechtecks oder auch eines gleichschenkligen
Trapezes, so entstehen Rauten.
Zum Beweis: Man zeigt, dass die Diagonalen aufeinander senkrecht stehen
und sich halbieren. |
Raute im Parallelogramm
... ... |
1 Zeichne ein beliebiges Parallelogramm.
2 Zeichne die beiden Diagonalen.
3 Halbiere die Winkel zwischen den Diagonalen und verbinde entsprechende
Schnittpunkte. |
Das Viereck ist eine Raute.
Zum Beweis: Die Diagonalen bilden eine Geradenkreuzung. Halbiert man
die Winkel, so stehen die Winkelhalbierenden aufeinander senkrecht.
Alle Formen
Hält man die horizontal liegende Diagonale e einer Raute fest
und wählt für die andere Diagonale f alle Längen zwischen
0 und e, so erhält man alle Formen einer Raute.
Man beachte den kleineren Innenwinkel: Er durchläuft die Werte zwischen
0° und 90°. Er ist geeignet, die Form einer Raute zu kennzeichnen.
Größen der Raute top
Das sind die Seite a, die Diagonalen e und f,
die Innenwinkel alpha und 180°-alpha, die Höhe
h,
der Umfang U, der Flächeninhalt A und der Radius des
Inkreises r.
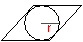Abgesehen vom Quadrat hat die Raute keinen Umkreis.
Eine Raute ist durch zwei Größen
gegeben. Die anderen Größen lassen sich aus ihnen berechnen.
1.Fall: Die Seite a und ein Innenwinkel alpha sind gegeben.
Zur Herleitung:
>Wende zur Bestimmung von e und f den Kosinussatz an.
>A=4*(1/2)*(e/2)*(f/2).
>Zeichne zur Berechnung der Höhe h in die Raute ganz links
ein rechtwinkliges Dreieck. Lies den Sinus ab.
>r=h/2
2.Fall: Die Diagonalen e und f sind gegeben.
Zur Herleitung:
>Wende den Satz des Pythagoras an: a²=(e/2)²+(f/2)².
>Setze die Fläche A aus den vier rechtwinkligen Dreiecken,
die die Diagonalen erzeugen, zusammen.
>Für den Flächeninhalt gilt (A=) a*h=(1/2)*e*f. Berechne
daraus die Höhe h.
> Berechne alpha mit dem Tangens, abgelesen im Dreieck aus e/2
und f/2.
>r=h/2
Figuren aus Rauten top
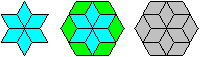
60°-Raute
Diese Raute hat die Innenwinkel 60° und 120°.
 |
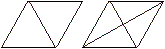Sie entsteht, wenn man ein gleichseitiges Dreieck an einer Seitenmitte
spiegelt.
Die beiden Diagonalen teilen die Raute in vier kongruente 30-60-90-Dreiecke. |
... ...
|
Aus sechs 60°-Rauten kann man einen Stern bilden. Verbindet man
die Zacken des Sterns mit sechs weiteren 60°-Rauten, so entsteht ein
regelmäßiges Sechseck. |
|
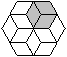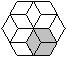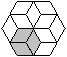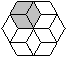Das Besondere dieses Sechsecks ist, dass es sechs halb so kleine Sechsecke
enthält. |
45°-Raute
... ... |
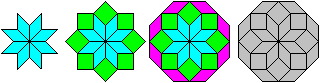Aus acht 45°-Rauten kann man einen Stern bilden.
Füllt man den Bereich zwischen den Zacken mit Quadraten und zwischen
den Quadraten mit Rauten, so entsteht ein regelmäßiges Achteck. |
|
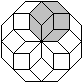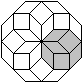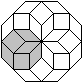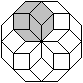Das Besondere dieses Achtecks ist, dass es acht halb so kleine Achtecke
enthält. |
Penrose Tiling
... ...
|
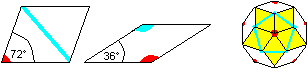
Aus fünf 72°-Rauten kann man einen fünfzackigen Stern
legen. Füllt man den Bereich zwischen den Zacken mit 36°-Rauten,
so ergibt sich ein regelmäßiges - Zehneck. |
... ...
|
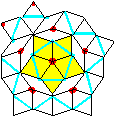
Das Zehneck wird noch einmal gelegt.
Dieses Mal gilt zusätzlich eine Dominoregel:
Die zehn Rauten werden mit Farbmarkierungen versehen. Gleiche Farben
sollen aneinander stoßen. |
... ...
|
Man kann die markierten Rauten rund um das Zehneck immer weiter legen.
Das Besondere ist, dass das zu einer "Parkettierung" der gesamten Ebene
führt und dass diese Parkettierung nichtperiodisch ist. Das ist erstaunlich,
denn bei so ziemlich allen Parkettierungen wiederholen sich bestimmte Bereiche.
Sie ist dann periodisch. |
Roger Penrose hat 1974 diese Parkettierung untersucht. N.G. de Bruijn bewies
1981 streng, dass mit den schon von Penrose angegeben Farbregeln eine periodische
Parkettierung der Ebene nicht möglich ist (Buch 1, Seite 58).
Bis heute ist ungeklärt, ob man mit einer einzelnen Figur die
Ebene nichtperiodisch parkettieren kann (Buch 2, Seite 214).
Eine Formel zur Raute top
... ... |
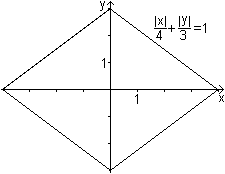Es ist möglich, eine Raute in einem Koordinatensystem nur durch
eine
Gleichung zu beschreiben.
Die Zahlen im Nenner der Gleichung findet man in der Zeichnung als halbe
Diagonalen.
|
|
|
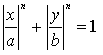
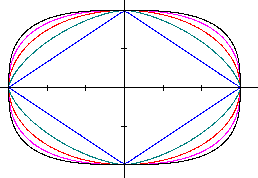
Die Raute ist der Grenzfall n=1 einer Lamé-Kurve. |
Mehr findet man auf meiner Seite Eilinien.
Rauten im Rechteck top
Mehr findet man auf meiner Seite Papierformat
A4
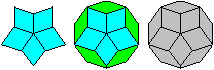
Körper aus Rauten top
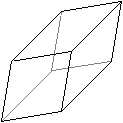
Aus sechs Rauten kann man einen Körper bilden. Er heißt
Parallelepiped oder Spat.
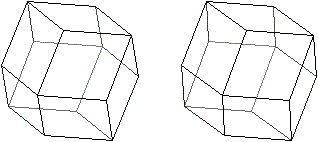
Aus 12 passenden Rauten entsteht das Rhombendodekaeder.
Raute im Internet top
Deutsch
mathepower
Raute berechnen
- online
Udo Hebisch (Mathematisches Café)
Rhombus
Wikipedia
Raute, Penrose-Parkettierung,
Rautenzeichen
Englisch
Drew Olbrich
Penrose Tiles
Steve Edwards
Aperiodic Tiling
Wikipedia
Rhombus, Penrose
tiling
Referenzen top
(1) F.L. Bauer, Einladung zur Mathematik, Deutsches Museum, München
(ISBN 3-924-18349-X)
(2) Ivars Peterson: Mathematische Expeditionen, Heidelberg-Berlin-New
York 1992 (ISBN 3-86025-044-2)
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
http://www.mathematische-basteleien.de/
©
2004 Jürgen Köller
top |
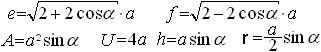
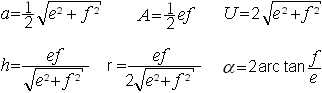
