|
Was ist eine Fakultät?
... ... |
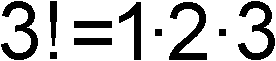Jede natürliche Zahl n hat eine Fakultät. Sie ist das Produkt
der natürlichen Zahlen, die kleiner oder gleich der Zahl n sind.
Man schreibt sie als n!=1*2*3*...*(n-1)*n und liest sie n Fakultät. |
Es ist zweckmäßig, 1!= 1 und auch 0!=1 zu definieren.
Man kann n! als Funktion mit dem Definitionsbereich D=|N, also als Folge,
sehen.
Dann ist an=n! oder rekursiv geschrieben ai=
i*ai-1. (i=1, 2, 3,..., n).
Das sind die ersten 15 Zahlen, wie sie
z.B. der Taschenrechner TI-30 liefert.
1!=1
2!=2
3!=6
4!=24
5!=120 |
6!=720
7!=5040
8!=40320
9!=362880
10!=3628800 |
11!=39916800
12!=479001600
13!=6227020800
14!=8.717829120*1010
15!=1.307674368*1012 |
Die beiden letzten Zahlen sind gerundet und in der wissenschaftlichen Schreibweise
angegeben.
Alle Zahlen sind zusammengesetzte Zahlen, die immer größer
werdende Primzahlen als Teiler haben. Darunter sind immer wieder Paare
von 2 und 5, die zu einer wachsenden Zahl von Endnullen führen.
Auf dieser Seite findet man überwiegend
Unterhaltsames zum Thema Fakultäten.
Große Fakultäten top
Taschenrechner
Fakultäten wachsen stark an. Oben ist 15! schon 13-stellig.
Die größte Zahl, die der Taschenrechner TI-30 angeben kann,
ist 69!=1,711224524*1098.
Dazwischen liegt eine Zahl, die man sich leicht merken kann, nämlich
25! ist ungefähr 1025, genauer 1.6*1025.
Google-Rechner
Größere Fakultäten bis 170! findet man, indem man sie
in das Suchfeld von Google eingibt und die Eingabetaste drückt. So
findet der Google-Rechner zum Beispiel 100 ! = 9.33262154 × 10157.
Tabellen
... ... |
Seit die Stochastik in die Schulen Einzug gehalten hat, haben Fakultäten
dort an Bedeutung gewonnen.
Zur Verfügung stehen heute Tabellen mit Fakultäten und
Binomialkoeffizienten. |
Zifferndarstellungen
Noch größere Fakultäten findet man unter anderen online
bei Wolfram Demonstrations Project oder bei Nitrxgen (URLs
unten) und dann auch noch in der genauen Ziffernschreibweise.
100!=9332621544394415268169923885626670049071596826438162146859296389521759999322
9915608941463976156518286253697920827223758251185210916864000000000000000000000000
Die Zahl hat 158 Ziffern, darunter 24 Endnullen.
Stirling-Formel
Man kann große Fakultäten auch mit Hilfe der Stirling-Formel
(und weiteren Näherungsformeln) bestimmen.
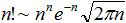Das Zeichen ~ ähnelt einem Gleichheitszeichen und soll ausdrücken,
dass die Terme sich mit größer werdenden Zahlen n immer
mehr annähern. Anders ausgedrückt: Der Quotient aus beiden Termen
geht gegen 1 für n gegen Unendlich.
Offensichtlich konvergiert der Quotient nicht stark, wie das folgende
Zahlenbeispiel zeigt.
50!=50^50*e^(-50)sqrt(2*pi*50) = 4,2*1064. - Es müsste
gelten 50!=3,0*1064.
Es ist bemerkenswert, dass die Konstanten
e und pi auftauchen. Im Hintergrund steht die Gamma-Funktion, mit deren
Hilfe man die Stirling-Formel beweisen kann.
Siehe auch (2), Seite 97f.
Anzahl der Endnullen top
Oben wird 100! mit 158 Ziffern und 24 Endnullen erwähnt.
Es stellt sich die Frage, wie man die Anzahl der Endnullen bestimmen
kann.
Es gilt folgende Regel.
Es genügt, die letzte Zahl, hier 100, zu untersuchen. Man dividiert
in einem ersten Schritt 100 durch 5, das ist 20. Dann dividiert man 20
wieder durch 5 und erhält 4. Die Summe der Quotienten ist 20+4=24,
und das ist die Anzahl der Endnullen.
Dieses Beispiel ist nicht typisch, weil es beim Dividieren keine Reste
gibt.
Ein zweites Beispiel ist 81! .
Man dividiert in einem ersten Schritt 81 durch 5, das ist 16. Der Rest
interessiert nicht.
Dann dividiert man 16 wieder durch 5 und erhält 3. Wieder ist
der Rest wegzulassen.
Die Summe der Quotienten ist 16+3=19, und das ist die Anzahl der Endnullen.
Anzahl der Ziffern top
Eine Spielerei mit Fakultäten besteht darin, die Anzahl ihrer
Ziffern zu bestimmen. (1)
Sie gestattet es dann, die Zahlen als Figuren zu schreiben.
1081396758240
2909005041013
0580032964972
0646107774902
5791441766365
7322653190990
5153326984536
5268082403397
7639893487202
9657993872907
8134368160972
8000000000000
0000000000000
|
1
081
39675
8240290
900504101
30580032964
9720646107774
902579144176636
57322653190990515
3326984536526808240
339776398934872029657
99387290781343681609728
000000 0000000000000000000
|
Die Zahl 105! hat 169 Ziffern.
Damit bilden die Ziffern ein 13*13-Quadrat.
Wegen 169=1+3+5+ ... +25=13² entsteht auch ein Dreieck. |
5
7 9
7 1 2
6 0 2 0
7 4 7 3 6
7 9 8 5 8 7
9 7 3 4 2 3 1
5 7 8 1 0 9 1 0
5 4 1 2 3 5 7 2 4
4 7 3 1 6 2 5 9 5 8
7 4 5 8 6 5 0 4 9 7 1
6 3 9 0 1 7 9 6 9 3
8 9 2 0 5 6 2 5 6
1 8 4 5 3 4 2 4
9 7 4 5 9 4 0
4 8 0 0 0 0
0 0 0 0 0
0 0 0 0
0 0 0
0 0
0
|
Die Zahl 81! hat 121 Ziffern.
Diese Anzahl ist die Summe der Dreieckszahlen d10+d11=55+66.
Deshalb kann man eine Figur aus zwei Dreiecken bilden. |
8 2 4 7 6 5
0 5 9 2 0 8 2
4 7 0 6 6 6 7 2
3 1 7 0 3 0 6 7 8
5 4 9 6 2 5 2 1 8 6
2 5 8 5 5 1 3 4 5 4 3
7 4 9 2 9 2 2 1 2 3
1 3 4 3 8 8 9 5 5
7 7 4 9 7 6 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0
|
Das Sechseck wird durch die Anzahl 91 der Fakultät 65! bestimmt.
Es gilt (d10+d11)- 2*d5=55+66-2*15=91 |
Primzahlen top
Die Zweierpotenzen 2n mit vielen Teilern führen zu
Primzahlen, wenn man sie um 1 erniedrigt oder um 1 erhöht. Das sind
dann die bekannten Mersenne-Zahlen 2n-1 oder Fermat-Zahlen 2n+1.
Die Frage ist, ob man auch Primzahlen erhält, wenn man mit Hilfe der
Fakultäten n!-1 und n!+1 bildet.
Bei N. J. A. Sloane findet man eine Antwort.
n!-1 ist für 3, 4, 6, 7, 12, 14, 30, 32, 33, 38, 94, 166, ...
eine Primzahl.
n!+1 ist für 1, 2, 3, 11, 27, 37, 41, 73, 77, 116, ... eine Primzahl.
Wilson-Satz
Für jede Primzahl gilt: Der Term (n-1)!+1 ist genau dann durch
n teilbar, wenn n eine Primzahl ist.
Zur Illustration des Satzes folgt eine Tabelle mit Beispielen. Die
roten Zahlen sind Primzahlen. Da geht die Division auf.
n
(n-1)!+1
[(n-1)!+1] : n |
2
2
1
|
3
3
3
|
4
7
1,8
|
5
25
5
|
6
121
20,2
|
7
721
103
|
11
3628801
329891
|
13
479001601
36846277
|
Es gilt weiter: Wenn der Term t(p)=(p-1)!+1
durch p² teilbar, so ist p eine Wilson-Primzahl.
Bei N. J. A. Sloane fndet man die folgenden, bis jetzt bekannten Wilson-Primzahlen
5, 13 und 563.
Ableitungen top
Die n-te Ableitung der Potenzfunktion f(x) = xn ist f (n)(x)
= n!
In der Taylor-Reihe treten Fakultäten
auf.
f(x)=f(a)+[f '(a)/1!](x-a)+[f ''(a)/2!](x-a)²+
... +[f(n)(a)/n!](x-a)n
Die Bedeutung dieser Formel liegt darin, dann man über sie zu
Reihenentwicklungen von u.a. ex, ln(1+x), sin(x), cos(x),
tan(x) und arc tan(x) gelangt. Man findet sie bei Wikipedia unter Taylor-Reihe.
Permutationen top
Gibt man n verschiedene Elemente einer Menge vor, so gibt es n! verschiedene
Anordnungen der Elemente.
In dieser Form begegnet man den Fakultäten in der Schule.
Beispiel
Es sei die Menge {a, b, c} gegeben.
Die Reihenfolge der drei Elemente kann man auf sechserlei Weise ändern,
nämlich zu abc, acb, bac, bca, cab, cba.
Das sind 3!=6 Anordnungen oder, wie man sagt, 3! Permutationen.
Will man allgemein beweisen, dass n Elemente
n! Permutationen haben, wählt man die Methode der vollständigen
Induktion.
Die Ausgangsmenge sei {a1, a2, a3,
..., an-1, an} oder zur Vereinfachung {1, 2, 3, ...
, n-1, n}.
Beweis
Voraussetzung: Die Anzahl der Permutationen von n Elementen sei n!.
Die Fälle n=1 und n=2 sind trivial.
Für n=3 gilt (s.o.): Es gibt 3!=6 Permutation von drei Elementen.
Es muss gezeigt werden, dass n+1 Elemente (n+1)! Permutationen haben
unter der Voraussetzung, dass n Elemente n! Permutationen haben.
Fügt man zu den n! Permutationen noch das Element n+1 hinzu, so
kann man es an n+1 Plätzen einer jeden der n! Permutationen
setzen. Also ergeben sich insgesamt n!*(n+1) Permutationen, und das ist
(n+1)!, wzbw.
Binomialkoeffizient
top
Pascal-Dreieck
 |
Binomialkoeffizienten sind die Zahlen
des Pascal-Dreiecks.
In der 2. Zeile stehen die Zahlen 1, 2, 1. Das sind die Vorzahlen von
(a+b)²=a²+2ab+b².
In der 3. Zeile stehen die Zahlen 1, 3, 3, 1. Das sind die Vorzahlen
von (a+b)³=a³+3a²b+3ab²+b³.
In der 4. Zeile stehen die Zahlen 1, 4, 6, 4, 1 aus (a+b)4=a4+4a³b+6a²b²+4ab³+b4.
...
In der n-ten Zeile stehen die Vorzahlen des ausgerechneten Terms zu
(a+b)n. |
Die Merkwürdigkeit des Dreiecks ist das Bildungsgesetz, dass nämlich
unter je zwei Zahlen ihre Summe liegt.
Die Zahl, die in der n-ten Zeile an der
k-ten Stelle steht, lässt sich explizit als "n über k" berechnen,
als ein Ausdruck, der aus Fakultäten gebildet wird.
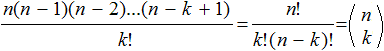
An mehreren Stellen meiner Homepage werden
sie verwendet.
Dreieckszahlen
Zahlenlotto
Setzt man k=6 und n=49, so gilt:
n!/[k!(n-k)!]
=49!/(6!43!)
=(49*48*47*46*45*44)/(2*3*4*5*6)...
=13 983 816. |
Beim Lotto 6 aus 49 berechnet man die Anzahl der Möglichkeiten,
sechs Zahlen anzukreuzen, als Binomialkoeffizient.
Mehr auf meiner Seite 13
983 816. Dort wird n!/[k!(n-k)!] hergeleitet. |
Taxi-Strecke
... ... |
In der Taxi-Geometrie stellt sich u.a.
das Problem, die Anzahl der Wege mit der Entfernung 8 von A nach B zu bestimmen. |
Somakörper
Kuriositäten top
| 4!+1=5² |
5!+1=11² |
7!+1=71² |
145=1!+4!+5! |
40585=4!+0!+5!+8!+5! |
10!=6!*7!=3!*5!*7! |
u.a. (1)
Fakultäten im Internet
top
Deutsch
Martin Steen
Fakultät
(Als Eingabe sind Zahlen zwischen 1 und 2500 zulässig)
Thomas Peters
Die Fakultäten
Wikipedia
Fakultät
(Mathematik), Fakultätsprimzahl,
Wilson-Primzahl,
Stirling-Formel,
Gammafunktion,
Binomialkoeffizient,
Taylor-Reihe
Englisch
Eric W. Weisstein (MathWorld)
Factorial,
Factorial
Prime
Jiel Beaumadier, Matej Hausenblas
All about factorial
notation
Nitrxgen
Factorial Calculator
(Allowed range: 0 to 200,000)
N. J. A. Sloane (On-Line Encyclopedia of Integer Sequences)
Factorial numbers: A000142,
Pascal's triangle read by rows: A007318
Numbers n such that n! - 1 is prime. A002982
Numbers n such that n! + 1 is prime. A002981
Wilson primes: primes p such that (p-1)! == -1 mod p^2. A007540
The Wolfram Demonstrations Project
Factorial
Wikipedia
Factorial, Factorial
prime, Wilson prime,
Stirling's
approximation, Gamma
function, Binomial
coefficient, Taylor
series
Referenzen top
(1) Martin Gardner: Geometrie mit Taxis, die Köpfe der Hydra und
andere mathematische Spielereien, Basel 1997
[ISBN 3-7643-5702-9]
(2) Jean-Paul Delahaye: Pi - Die Story, Basel, Boston, Berlin 1999
[ISBN 3-7643-6056-9]
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
http://www.mathematische-basteleien.de/
©
2009 Jürgen Köller
top |
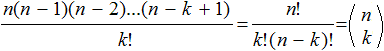
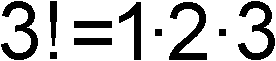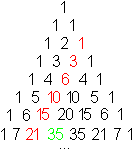
