|
Was ist der Schwerpunkt einer Figur?
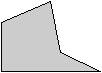
Der Schwerpunkt ist ein besonderer Punkt eines Körpers.
... ... ...
|
Er soll an einer dünnen, starren, homogenen Scheibe
in Fünfeckform erklärt werden.
Homogen heißt, dass die Masse gleichmäßig
verteilt ist, dass also die Masse pro Flächeneinheit an jeder Stelle
gleich ist.
Man kann sich vorstellen, dass die Scheibe aus Pappe
ist. |
...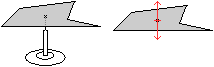 ... ... |
Man balanciert die Scheibe so auf einer spitzen Nadel,
dass sie horizontal schwebt. Der Punkt, in dem die Nadel die Scheibe berührt,
heißt Schwerpunkt.
In der Nadelspitze greift die Gewichtskraft an, hervorgerufen
durch die Schwerkraft. Die gleich große, von der Nadel aufgebrachte
Gegenkraft
hält den Körper. Dabei spielt es keine Rolle, welche Form die
Scheibe hat. Man kann sich vorstellen, dass die gesamte Masse in einem
Punkt konzentriert ist. |
Auf dieser Seite geht es
um die Bestimmung von Schwerpunkten flächenartiger Körper.
Sie sind beispielhaft auch für die Bestimmung von
Schwerpunkten linienartiger oder räumlicher Körper.
Indifferentes
Gleichgewicht
top
Das Balancieren der Scheibe auf einer Nadelspitze hat
seine Tücken.
...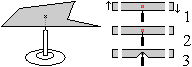 ... ...
... |
1 Setzt man die Scheibe vorsichtig auf die Spitze, so
misslingt das. Die Scheibe kippt, da der Schwerpunkt (rot) über dem
Auflagepunkt liegt und durch die Gewichtskraft leicht ein kippendes Drehmoment
entsteht.
2 Man könnte manipulieren und die Spitze in die
Scheibe hinein stechen, wenn sie zum Beispiel aus Pappe ist. Das ist indiskutabel.
3 Eine stabile Lage entsteht dadurch, dass man in die
Scheibe von unten eine Vertiefung anbringt, in die die Spitze dann so weit
hineinragt, dass der Auflagepunkt über dem Schwerpunkt liegt. |
...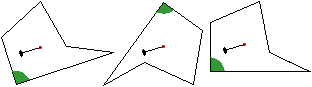 ... ... |
Theoretisch bleibt die Scheibe in jeder Lage stehen,
wenn sie genau im Schwerpunkt unterstützt wird. Sie ist im indifferenten
Gleichgewicht.
Praktisch gelingt es leicht, der Scheibe jede vertikale
Lage zu geben. Man sticht im Schwerpunkt durch die Scheibe und hält
sie mit einer Nadel. |
Experimentelle
Bestimmung des Schwerpunktes top
Der Schwerpunkt liegt immer unter dem Aufhängepunkt
eines Körpers. Wäre das nicht der Fall, so träte ein Drehmoment
auf, das den Körper in diese Lage treibt. - Die Scheibe ist im stabilen
Gleichgewicht.
...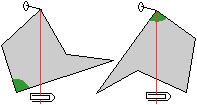 ... ... |
Das macht man sich zunutze.
Man hängt die Scheibe und einen Faden zweimal an
Ecken auf.
An das andere Ende des Fadens klemmt man eine Büroklammer.
Den Verlauf der Fäden markiert man durch Linien.
Sie sind Bestimmungslinien für den Schwerpunkt. |
...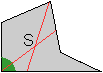 |
Die beiden Schwerlinien treffen sich im Schwerpunkt. |
Dieses Verfahren wird auch
auf meiner Seite
Geographischer Mittelpunkt
beschrieben.
Schwerpunkt
zweier Massenpunkte top
Ehe einzelne Figuren untersucht werden, soll vorweg ein
grundlegendes Problem erörtert werden.
...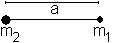 ... ... |
Gegeben seien zwei Massenpunkte m1 und m2
in
der Entfernung a.
Die "Verbindungsstange" sei gewichtslos.
Wo liegt der Schwerpunkt dieser Hantel? |
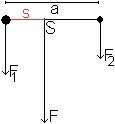
Der Schwerpunkt sei S.
... .. ..
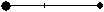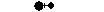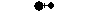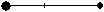 . .
|
Man stelle sich vor, die Hantel werde im Schwerpunkt
unterstützt.
Es herrscht in S ein Gleichgewicht der Kräfte:
Im Auflagepunkt S entsteht die Gegenkraft zu F=F1+F2
nach oben.
Es herrscht ein Gleichgewicht der Drehmomente:
Das linksdrehende Drehmoment sF1 ist genau
so groß wie das rechtsdrehende Drehmoment (a-s)F2.
Aus sF1=(a-s)F2 folgt s=(aF2)/(F1
+F2) oder a-s=(aF1)/(F1 +F2).
Da die Gewichtskräfte proportional zu den Massen
sind, gilt auch s=(am2)/(m1+m2). |
Die letzte Formel kann man
einem Zahlenstrahl anpassen.
...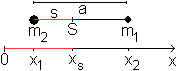 ... ... |
Es gilt a=x2-x1 und s=xs-x1.
Dann ergibt sF1=(a-s)F2 die Gleichung
(xs-x1)F1=[(x2-x1)-(xs-x1)]F2.
Daraus folgt xs=(x1F1+x2F2)/(F1
+F2) oder xs=(x1m1+x2m2)/(m1+m2). |
... ... ... |
Wird die Lage der Massepunkte in einem Koordinatensystem
angegeben durch S1(x1|y1) und S2(x2|y2),
liegt der Schwerpunktes an der Stelle xs=(x1m1+x2m2)/(m1+m2)
und ys=(y1m1+y2m2)/(m1+m2). |
Diese Formel wird unten angewandt.
Schwerpunkt
punktsymmetrischer Figuren top
... ... ... |
Die Bestimmung der Lage des Schwerpunktes punktsymmetrischer
bzw. drehsymmetrischer Figuren bereitet keine Mühe, da dieser Punkt
mit dem Symmetriezentrum zusammenfällt. - Der Kreisring ist das Beispiel
einer Figur, deren Schwerpunkt außerhalb der Figur liegt. |
Ist eine Figur achsensymmetrisch,
so liegt ihr Schwerpunkt auf der Symmetrieachse.
Schwerpunkt
eines Dreiecks
top
Vorüberlegung
...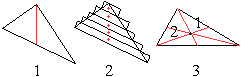 .... .... |
Man kann den Schwerpunkt eines Dreiecks wie oben durch
Aufhängen bestimmen. |
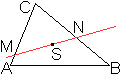
1 Man hängt also das Dreieck an einer Ecke auf.
2 Dieses Vorgehen kann ein Gedankenexperiment bleiben.
Man muss sich vorstellen, dass das Dreieck in beliebig viele Streifen aufgeteilt
ist. In der Zeichnung bleibt es bei der Anzahl Fünf. Dann stellt
sich das Dreieck so ein, dass die Mittelpunkte der Streifen unter dem Aufhängepunkt
liegen. - Der Schwerpunkt liegt danach auf einer Seitenhalbierenden.
3 Diese Überlegung gilt für die anderen Ecken
auch. Der Schwerpunkt ist also der gemeinsame Schnittpunkt der Seitenhalbierenden,
also der Verbindungslinien der Eckpunkte mit den gegenüberliegenden
Seitenmitten.
Zeichnerische
Bestimmung
Man ermittelt den Schwerpunkt eines
Dreiecks zeichnerisch, indem man den Schnittpunkt der Seitenhalbierenden
sucht.
Rechnerische
Bestimmung
Über die Seitenhalbierenden lässt sich der
Schwerpunkt auch berechnen.
Man verwendet dabei die zusätzliche Eigenschaft,
dass sich die Seitenhalbierenden im Verhältnis 2:1 schneiden.
... ... ...
|
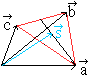
Für die Rechnung bieten sich Vektoren an.
Die Eckpunkte eines Dreiecks seien also durch Ortsvektor
a,
Ortsvektor b und Ortsvektor c gegeben.
|
Dann gilt für den Ortsvektor s:.
|
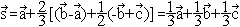 |
|
Das Ergebnis wird auf ein Dreieck, das in einem kartesischen
Koordinatensystem gegeben sein soll, übertragen.
Die Punkte A(ax|ay), B(bx|by)A(cx|cy)
sind gegebenen.
Dann lauten die Formeln für den Schwerpunkt S(xs|ys):
xs=(ax+bx+cx)/3
und
ys=(ay+by+cy)/3.
Zahlenbeispiel
...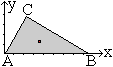 ... ...
|
Die Eckpunkte des Dreiecks sind A(0|0), B(8,5|0), C(2,3|3,8).
Dann ist xs=(0+8,5+2,3)/3=3,6 und ys=(0+0+3,8)/3=3,8/3=19/15=~1,3.
Der Schwerpunkt ist markiert.
|
Schwerpunkt
von Vierecken top
Zeichnerische Bestimmung
...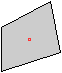 ... ... |
Gegeben ist ein beliebiges Viereck. Der Schwerpunkt ist
schon eingezeichnet. |
Man findet ihn über Dreiecke.
....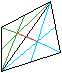 ..... ..... |
Zuerst teilt man das Viereck durch eine Diagonale in
zwei Teildreiecke, bestimmt für jedes Dreieck die Schwerpunkte und
verbindet sie. |
....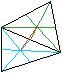 ..... ..... |
Man teilt das Viereck durch die andere Diagonale in zwei
Teildreiecke, bestimmt wieder die Schwerpunkte und verbindet sie. |
....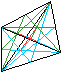 ..... ..... |
Der Schnittpunkt der roten Verbindungslinien ist der
Schwerpunkt des Vierecks. |
Rechnerische
Bestimmung
...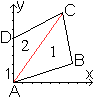 ... ... |
Gegeben ist wieder dasselbe Viereck, jetzt in einem kartesischen
Koordinatensystem.
Seine Eckpunkte sind A(0|0), B(6|2), C(5|7), D(0|5). |
Man führt die Schwerpunktbestimmung auf Dreiecke zurück.
... ... ... |
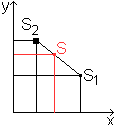
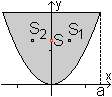
Zuerst teilt man das Viereck durch eine Diagonale in
zwei Teildreiecke. Man bestimmt für jedes Dreieck den Schwerpunkt.
Es gilt xS1=(6+5)/3=11/3, yS1=(2+7)/3=3 und xS2=5/3,
yS2=(7+5)/3=4.
Der Schwerpunkt liegt auf der Verbindungslinie a=S1S2,
aber wo? |
Die beiden Dreiecke können als punktförmige Körper
mit den Massen m1 und m2 aufgefasst werden. Für
sie gelten die Formeln xs=(x1m1+x2m2)/(m1+m2)
und ys=(y1m1+y2m2)/(m1+m2).
Bedenkt man noch, dass für eine homogene Figur die
Masse m und der Flächeninhalt A proportional sind, so heißen
die Formeln xs=(x1A1+x2A2)/(A1+A2)
und ys=(y1A1+y2A2)/(A1+A2).
Also muss man noch die Flächeninhalte
der Dreiecke bestimmen.
...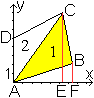 ... ... |
Man bestimmt sie z.B. nach der Trapezmethode, die am
Dreieck ABC erklärt wird.
Man addiert die Flächeninhalte von Viereck EFBC
und Dreieck AEC und subtrahiert dann das Dreieck AFB.
Es ergibt sich A1=5*7/2+(7+2)/2*1-6*2/2=16.
Analog erhält man A2=(7+5)/2*5-5*7/2=25/2.
Das führt zu s=a(25/57) oder s/a=25/57. |
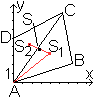 |
Es gilt nach der Zeichnung S1(xS1|
yS1), S1(xS2| yS2) und S(xS|
yS).
Somit ist xs=(xS1A1+xS2A2)/(A1+A2)=[(11/3)*16+(5/3)*(25/2)]/(16+25/2)=53/19
und ys=(yS1A1+yS2A2)/(A1+A2)=[3*16+4*(25/2)]/(16+25/2)=196/57 |
Ergebnis: Der Schwerpunkt ist S(53/19|196/57).
Diese Methode kann auf Vielecke
erweitert werden, zum Beispiel auf das Fünfeck oben.
Schwerpunkt
eines Drachens
...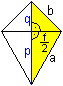 ... ... |
Hier sind noch einmal die Stücke eines Drachenvierecks
von einer anderen Stelle meiner Homepage.
Der Schwerpunkt liegt auf der Symmetrieachse, und zwar
im unteren Teildreieck des Drachens. |
... ... ... |
Zur genauen Bestimmung dreht man das Drachenviereck um
-90° und betrachtet zwei Teildreiecke. Sie haben Schwerpunkte rechts
und links der vertikalen Diagonalen in den Entfernungen q/3 und p/3. Ihre
Entfernung ist q/3+p/3. |
...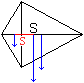 ... ... |
Es ergibt sich das Bild des gemeinsamen Schwerpunktes
zweier Massenpunkte von oben.
Mit A1= (1/2)f*p/2 und A2=(1/2)f*q/2
ergibt sich s=a*A2/(A1+A2)=aq/(p+q). |
Schwerpunkt
eines Trapezes
...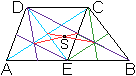 ... ... |
Man findet den Schwerpunkt durch eine Konstruktion wie
oben beim Viereck.
Man zerlegt das Trapez zweimal, und zwar in das Parallelogramm
AECD und das Dreieck EBC und in das Dreieck AED und das Parallelogramm
EBCD. Man bestimmt die Schwerpunkte und verbindet sie paarweise.
Der Schnittpunkt der Verbindungslinien ist der Schwerpunkt. |
...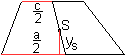 ... ... |
Der Tabellenwert ist ys=(1/3h)(a+2c)/(a+c). |
Eine weitere Konstruktion
findet man auf der Wikipedia-Seite
Trapez.
Schwerpunktberechnungen
durch Integrale top
Zur Herleitung der Formeln
Oben wurde zum Schwerpunkt zweier Massenpunkte die folgende
Aussage gemacht.
... ... ... |
Wird die Lage der Massepunkte in einem Koordinatensystem
angegeben durch S1(x1|y1) und S2(x2|y2),
liegt der Schwerpunktes an der Stelle xs=(x1m1+x2m2)/(m1+m2)
und ys=(y1m1+y2m2)/(m1+m2). |
Die Formel erweitert man
auf eine Anordnung von n Massenpunkten.
......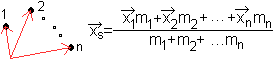 |
Die Lage des Schwerpunkts wird durch einen Ortsvektor
angegeben. |
......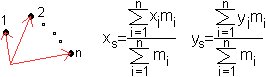 |
Für das praktische Rechnen sind Koordinatengleichungen
vorzuziehen. |
...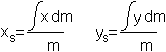 ... ... |
Lässt man die Anzahl der Massenpunkte über
alle Grenzen gehen, so erhält man ein Kontinuum, einen homogenen Körper.
Die Grenzwerte sind Integrale. |
...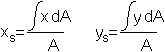 ... ... |
Bedenkt man noch, dass für eine homogene Figur Masse
und Flächeninhalt proportional sind, ergeben sich Formeln, mit denen
man wie in den nächsten Abschnitten z.B. Schwerpunkte eines Parabelabschnittes
oder eines Halbkreises berechnet. |
Schwerpunkt
eines Parabelabschnitts
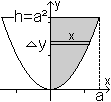
Gegeben ist ein Parabelabschnitt, begrenzt von y=x²,
y=h und x=0. Gesucht ist der Schwerpunkt S.
Erste Koordinate
...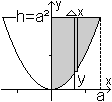 |
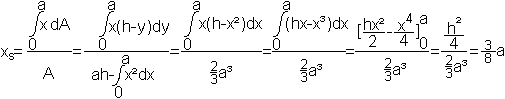
|
Zweite
Koordinate
... |
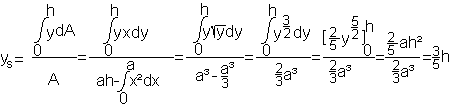
|
Ergebnis: Der Schwerpunkt
liegt an der Stelle S[(3/8)a | (3/5)h].
... ... ... |
Betrachtet man den Parabelabschnitt, der von der Parabel
und y=h begrenzt wird, so liegt sein Schwerpunkt einmal auf der y-Achse.
Zum anderen ist die Ordinate 3h/5 wie oben. |
Schwerpunkt
eines Halbkreises
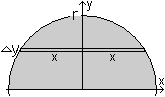
Gegeben ist ein Halbkreis mit dem Radius r. Gesucht ist
der Schwerpunkt S.
... ... ... |
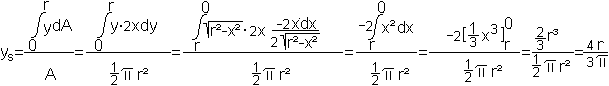
"dx statt dy" heißt, die Grenzen in sqrt(r²-0²)=r
und sqrt(r²-r²)=0 zu ändern. |
Ergebnis: Die erste Koordinate
ist aus Gründen der Symmetrie xs=0.
Die zweite Koordinate ist ys=(4r)/(3*Pi) oder
angenähert ys=0,42r.
...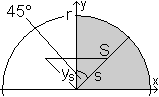 ... ... |
Mit Hilfe des Halbkreises gelangt man nach nebenstehender
Zeichnung zum Schwerpunkt eines Viertelkreises.
Es gilt cos(45°)=ys/s oder s=ys/cos(45°)=[4*sqrt(2)r]/(3*Pi). |
Schwerpunkt
einer Platte mit Loch top
...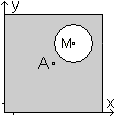 ... ... |
Gegeben ist eine Platte der Seitenlänge 10. Ihre
Mitte liegt bei A(5|5). Die Platte hat ein kreisrundes Loch mit dem Durchmesser
2. Der Mittelpunkt des Kreises liegt an der Stelle M(7|7).
Gesucht ist der Schwerpunkt der Platte.
Lösungsweg: Es geht um den gemeinsamen Schwerpunkt
zweier Massenpunkte.
Das Besondere ist, dass die Kreisfläche ein negatives
Vorzeichen bekommt. |
Lösung:
Es gilt xs=(x1m1-x2m2)/(m1-m2)=(x1A1-x2A2)/(A1-A2)
Die Flächeninhalte sind A1=100 und A2=Pi,
die Abszissen x1=5 und x2=7.
xs=[5*100-7*Pi]/(100-Pi)=(500-7*Pi)/(100-Pi)
oder angenähert 4,71.
Es ist ys=xs.
xs=[5*100-7*(4*Pi)]/(100-4*Pi)=(500-28*Pi)/(100-4*Pi)=(250-14*Pi)/(50-2*Pi)
oder angenähert 4,94.
Es ist ys=xs.
Ergebnis: Der Schwerpunkt
liegt angenähert bei (4,94|4,94).
Schwerpunkt im
Internet top
Deutsch
Arndt Brünner
Der
Schwerpunkt des Dreiecks
Lehrstuhl A für Mathematik, RWTH Aachen
Der
Schwerpunktsatz (eines Dreiecks), Animation
Randolf Rehfeld
Schwerpunkte
Wikipedia
Schwerpunkt,
Massenmittelpunkt,
Schwerpunktsatz,
Standfestigkeit,
Gleichgewicht
(Physik), Erde-Mond-Schwerpunkt
Englisch
eFunda
Common
Shapes
Eric W Weisstein (MathWorld)
Geometric
Centroid, Pappus's
Centroid Theorem
Wikipedia
Centroid,
Center
of mass,
Pappus's
centroid theorem (Guldinus theorem), List
of centroids
Referenzen
top
(1) I.N. Bronstein/K.A.Semendjajew: Taschenbuch der Mathematik,
Moskau Leipzig, 1987
(2) Richard Doerfling: Mathematik für Ingenieure
und Techniker, München 1965
(3) Mende/Simon: Physik Gleichungen und Tabellen, München
1976
Feedback: Emailadresse
auf meiner Hauptseite
URL meiner
Homepage:
http://www.mathematische-basteleien.de/
©
2007 Jürgen Köller
top |
 ...
... ...
... ...
...
 ...
... ...
...


 ..
..
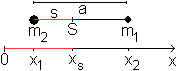 ...
... ...
... ....
.... ...
... ...
... ...
... .....
..... .....
..... .....
.....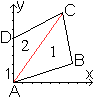 ...
...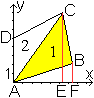 ...
...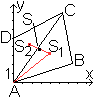
 ...
... ...
... ...
... ...
... ...
...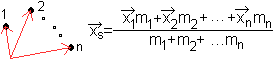
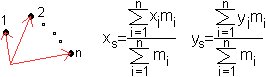
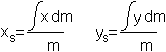 ...
...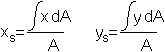 ...
...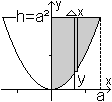
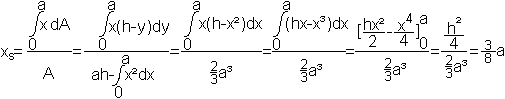

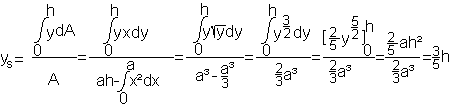
 ...
... ...
...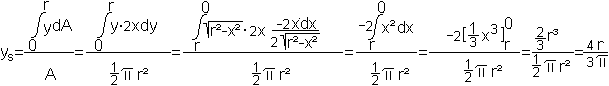
 ...
... ...
... ...
...