|
Achsen- und punktsymmetrische
Figuren
|
Was sind achsen- und punktsymmetrische
Figuren?
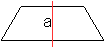
Eine Figur ist achsensymmetrisch,
wenn es möglich ist, einen Spiegel so an eine Hälfte der Figur
senkrecht zur Zeichenebene zu stellen, dass ihr Spiegelbild und die
andere Hälfte zur Deckung kommen.
Ersetzt man den Spiegel durch eine Glasscheibe, so kann
man Urbild und Bild gleichzeitig sehen, wenn auch nicht so deutlich.
Gleichschenkliges Trapez
.
.

|
Eine Figur ist punktsymmetrisch,
wenn sie einen Punkt hat, um den die Figur so um 180° gedreht werden
kann, dass sie mit der Ausgangsfigur zur Deckung kommt.
Man sagt auch, sie ist drehsymmetrisch der Ordnung
2.
...
Parallelogramm


|
Anders ausgedrückt:
Eine Figur ist achsensymmetrisch,
wenn sie bei einer Spiegelung an einer Geraden in sich selbst übergeht.
 Die Gerade heißt Spiegelachse oder einfach Achse.
Die Gerade heißt Spiegelachse oder einfach Achse.
 |
Eine Figur ist punktsymmetrisch,
wenn sie bei einer Spiegelung an einem Punkt in sich selbst übergeht.
 Der Punkt heißt Spiegelzentrum oder einfach Zentrum.
Der Punkt heißt Spiegelzentrum oder einfach Zentrum.
 |
Grundlagen
top
Den beiden Formen symmetrischer Figuren liegen zwei Kongruenzabbildungen
der Ebene auf sich selbst zu Grunde.
Das sind die Achsenspiegelung und die Punktspiegelung.
|
Achsenspiegelung
|
Punktspiegelung..
|
Spiegelung eines Punktes
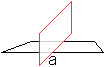
Eine Gerade a sei als Achse gegeben.
Dann findet man zum Punkt P den Bildpunkt P', indem man
zu a ein Senkrechte zeichnet und auf der Gegenseite den Punkt P' im gleichen
Abstand ermittelt.
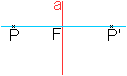 Die Strecke PP' heißt Zuordnungslinie. F halbiert PP'.
Die Strecke PP' heißt Zuordnungslinie. F halbiert PP'.
Spiegelt man den Punkt P' an a, so erhält man wieder
P, P''=P. Die Abbildung ist involutorisch.

|
Spiegelung eines Punktes
Ein Punkt Z als Zentrum sei gegeben.
Dann findet man zum Punkt P den Bildpunkt P', indem man
die Gerade PZ zeichnet und auf der Gegenseite den Punkt P' in gleicher
Entfernung ermittelt.
 Die Strecke PP' heißt Zuordnungslinie. Z halbiert PP'.
Die Strecke PP' heißt Zuordnungslinie. Z halbiert PP'.
Spiegelt man den Punkt P' an Punkt Z, so erhält
man wieder P, P''=P. Die Abbildung ist involutorisch.
.
.
 |
Zeichnen eines Bildpunktes
Gut geeignet ist das Geodreieck.
Doch es ist Tradition zu konstruieren.
Gegeben sei die Achse a und der Punkt P.
Konstruiere den Bildpunkt P'.
 >Zeichne einen Kreis um P mit passendem Radius.
>Zeichne einen Kreis um P mit passendem Radius.
Er schneidet die Achse in den Punkten A und B.
>Zeichne um Punkt A einen Kreis mit dem gleichen Radius.
>Zeichne um Punkt B einen Kreis mit dem gleichen Radius.
>Der Schnittpunkt der Kreise ist der gesuchte Punkt P'.
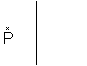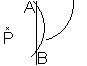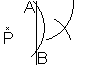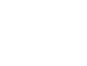

|
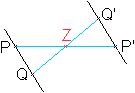
Gegeben sei das Zentrum Z und der Punkt P.
Konstruiere den Bildpunkt P'.
 >Zeichne die Gerade PZ.
>Zeichne die Gerade PZ.
>Zeichne um Punkt Z einen Kreis mit dem Radius PZ.
> Der Schnittpunkt von Gerade und Kreis ist der gesuchte
Punkt P'.
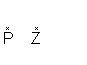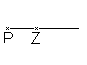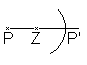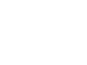
..
.

|
Spiegelung einer Strecke
Es genügt, nur die Endpunkte der Strecke zu spiegeln.
Die Strecke PQ geht nämlich wieder in eine (kongruente) Strecke P'Q'
über.
 Die Geraden PQ und P'Q' schneiden sich in einem Punkt
der Achse.
Die Geraden PQ und P'Q' schneiden sich in einem Punkt
der Achse.

|
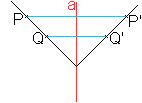
Es genügt, nur die Endpunkte der Strecke zu spiegeln.
Die Strecke PQ geht nämlich wieder in eine (kongruente) Strecke P'Q'
über.
 Die Geraden PQ und P'Q' sind parallel.
Die Geraden PQ und P'Q' sind parallel.
.

|
Fixgerade
Spiegelung eines Dreiecks
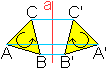 Ein Dreieck geht bei einer Geradenspiegelung in ein kongruentes
Dreieck über.
Ein Dreieck geht bei einer Geradenspiegelung in ein kongruentes
Dreieck über.
Dabei wird der Richtungssinn vertauscht. Wie man auch
das Dreieck ABC in der Ebene bewegt, man kann es nicht mit Dreieck A'B'C'
zur Deckung bringen. Man kommt um eine Klappung im Raum, z.B. mit der Achse
als Scharnier, nicht herum.
 |
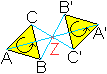 Ein Dreieck geht bei einer Punktspiegelung in ein kongruentes
Dreieck über.
Ein Dreieck geht bei einer Punktspiegelung in ein kongruentes
Dreieck über.
Dabei wird der Richtungssinn beibehalten.
Man kann das Dreieck ABC in der Ebene so bewegen, dass
es mit Dreieck A'B'C' zur Deckung kommt.
 |
Es gibt eine weitere Spiegelung,
die Kreisspiegelung oder Inversion.
Erzeugung von Figuren
top
Zeichnung
Einfache symmetrische Figuren erzeugt
man punktweise.
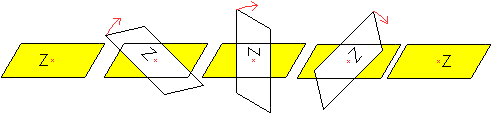
Ein Drachenviereck z.B. erzeugt man, indem man ein Dreieck
ABC an einer Seite spiegelt.
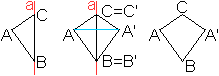
 |
Ein Parallelogramm z.B. erzeugt man, indem man ein Dreieck
ABC am Mittelpunkt einer Seite "punktspiegelt".
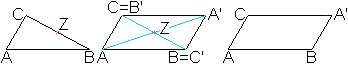

 |
Zeichenprogramm
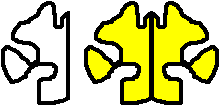
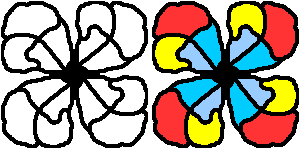
Unregelmäßige symmetrische Figuren kann man
mit einem Zeichenprogramm erzeugen. Ich wähle MSPaint, weil es unter
Windows unter Start/Zubehör für jedermann, der Windows benutzt,
zugänglich ist.
Man gibt also die halbe Figur vor und ergänzt sie entsprechend.
Zeichenprogramm
Es gibt zur Symmetrie im Internet Applets, mit denen
man spielen kann.
Ein Beispiel ist die Seite MathsIsFun.com (URL unten).
Scherenschnitte

|

Hannah, 4 Jahre
|
Achsen-
und punktsymmetrische Figuren
top
Es gibt Figuren wie das Rechteck, die sowohl achsensymmetrisch
als auch punktsymmetrisch sind.
... ... ... |
Für diese Figuren gibt es zwei aufeinander senkrecht
stehende Symmetrieachsen. Das Zentrum liegt im Schnittpunkt dieser beiden
Achsen. |
Zum Beweis
...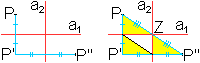 ... ... |
Die erste Zeichnung zeigt, wie ein Punkt P zuerst an
der einen Achse, dann an der anderen Achse gespiegelt wird. Die zweite
Zeichnung stellt dar, wie man direkt von Punkt P zu Punkt P'' über
eine Punktspiegelung gelangt. Kongruente Dreiecke stellen sicher, dass
Punkt P und P'' auf einer Geraden liegen und dass PZ=ZP'' gilt. |
Buchstaben und
Symmetrie top
Buchstaben als Figuren
Das Parade-Beispiel symmetrischer Figuren sind bestimmte
große Buchstaben.
achsensymmetrisch rot
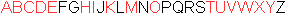

|
punktsymmetrisch rot


|
Die Buchstaben H, I,
O
und X sind sowohl achsen- als auch punktsymmetrisch.
Und hier?
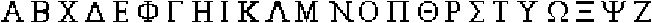
Palindrome
Die Symmetrie kann man auf Wörter (und Sätze)
übertragen. Dann kommt man zu den Palindromen.
Ein Palindrom ist gewöhnlich ein Wort, das gleich
bleibt, auch wenn man es von rechts nach links liest. Bekannte Wörter
sind Otto, Anna oder Reliefpfeiler.
Diese Eigenschaft kann man auf Zahlen übertragen.
So sind 1001 oder 1.234.321 Palindrome.
Zahlen wie 80808 oder 69896 sind etwas Besonderes: Sie
sind auch als Figuren achsen- bzw. punktsymmetrisch.
Die
folgende "Spiegelschrift" ist nicht symmetrisch, geht aber durch eine Spiegelung
aus einer Schreibfigur hervor.
Spiegelschrift
Wenn man als Rechtshänder
mit der linken Hand so schreibt wie mit der rechten und nicht nachdenkt,
gelangt man zur Spiegelschrift.
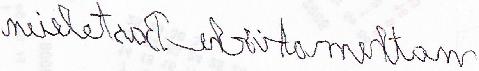 Das Geschriebene wird besser lesbar, wenn man es in einem
Spiegel betrachtet.
Das Geschriebene wird besser lesbar, wenn man es in einem
Spiegel betrachtet.
Rückwärts
sprechen
Eine beliebte Station der Wanderausstellung Mathematik
zum Anfassen ist eine Anordnung mit Mikrofon und Wiedergabegerät.
Man wird aufgefordert, den eigenen Namen rückwärts zu sprechen.
Anschließend kann man sich das Gesagte wieder anhören.
Weitere
Beispiele symmetrischer Figuren
top
In diesem Kapitel zeige ich symmetrische Figuren meiner
Internetseiten. Da ist kein Mangel.
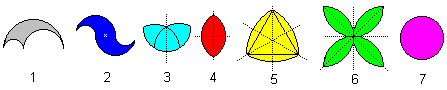
Kreisfiguren
|
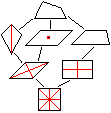
Hierarchie der Vierecke
|
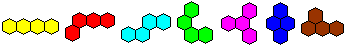
Polywaben
Symmetrische Kurven
top
Es gelten die Sätze:
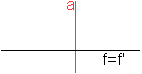
Eine Funktion f ist achsensymmetrisch bezüglich
der y-Achse, wenn f(x)=f(-x) für alle x-Werte des Definitionsbereichs
gilt..
Das Standard-Beispiel ist f(x)=x². |
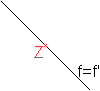
Eine Funktion f ist punktsymmetrisch bezüglich
des Nullpunkts, wenn f(x)=-f(-x) für alle x-Werte des Definitionsbereichs
gilt.
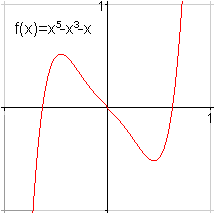
Das Standard-Beispiel ist f(x)=x³. |
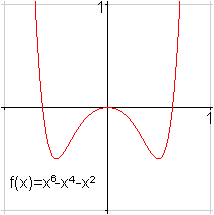
Zwei aufwändigere Beispiele.
Unter den Relationen F(x,y)=0 findet man solche mit Graphen,
die achsen- und zugleich punktsymmetrisch sind.
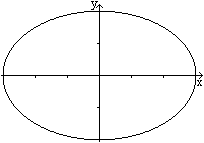
Ellipse
x²/9+y²/4-1=0
|
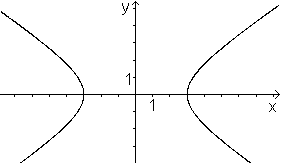
Hyperbel
x²/9-y²/4-1=0
|
Sie sind achsensymmetrisch bezüglich der x- und y-Achse
und punktsymmetrisch bzgl. des Nullpunkts.
Es gilt F(x,y)=F(-x,-y)
Symmetrische Körper
top
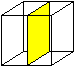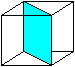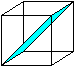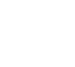
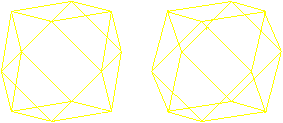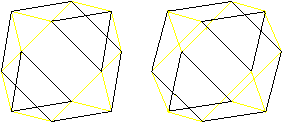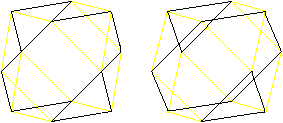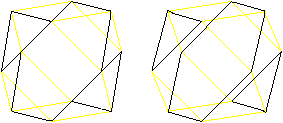
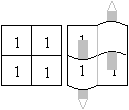
Wenn man ein Quadrat wie in den Zeichnungen angegeben
faltet, gelangt man zu zwei symmetrischen Körpern.
(1) Seite 210f. und 219f.
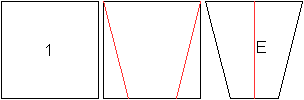 Faltet man an den roten Linien nach oben und richtet die
Streifen rechts und links vertikal nach oben aus, so entsteht ein symmetrischer
Körper. Denkt man sich eine Mittelebene E, so ist jeder Punkt des
Körpers spiegelsymmetrisch zu einem anderen bzgl. dieser Ebene.
Faltet man an den roten Linien nach oben und richtet die
Streifen rechts und links vertikal nach oben aus, so entsteht ein symmetrischer
Körper. Denkt man sich eine Mittelebene E, so ist jeder Punkt des
Körpers spiegelsymmetrisch zu einem anderen bzgl. dieser Ebene.
Körper dieser Art sind spiegelsymmetrisch.
 |
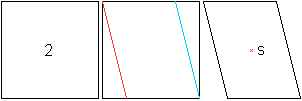 Faltet man an der roten Linie nach oben und an der blauen
nach unten und richtet die Streifen rechts und links vertikal nach oben
und unten aus, so entsteht ein symmetrischer Körper. Dreht man ihn
um 180° um die senkrecht auf der Quadratebene stehenden Achse S, so
geht er in sich selbst über.
Faltet man an der roten Linie nach oben und an der blauen
nach unten und richtet die Streifen rechts und links vertikal nach oben
und unten aus, so entsteht ein symmetrischer Körper. Dreht man ihn
um 180° um die senkrecht auf der Quadratebene stehenden Achse S, so
geht er in sich selbst über.
Körper dieser Art sind drehsymmetrisch der Ordnung
2.
 |
.. .... .... |
Martin Gardner schreibt in (1):
"Ich habe einmal behauptet, dass ein dreidimensionaler
Körper, der keine Symmetrieebene hat, ... nicht mit seinem Spiegelbild
zur Deckung gebracht werden könne... Diese Aussage ist falsch!"
Der nebenstehende Körper ist drehsymmetrisch der
Ordnung 2 und nicht spiegelsymmetrisch. Er geht trotzdem in sich selbst
über, wenn man ihn an der Quadratebene spiegelt. |
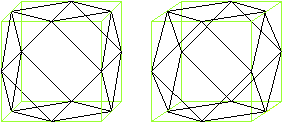
Ein weniger ausgefallenes
Beispiel eines symmetrischen Körpers ist der Würfel.
Er ist sowohl spiegelsymmetrisch als auch drehsymmetrisch.
Er hat neun Symmetrieebenen und neun passende Symmetrieachsen.
Kuboktaeder in 3D
Symmetrische
Figuren im Internet top
Deutsch
Universität Bayreuth - Lehrstuhl für Mathematik
und ihre Didaktik
Achsensymmetrische
Figuren
Wikipedia
Achsensymmetrie,
Spiegelung
(Geometrie), Symmetrisch,
Symmetrieachse,
Involution
(Mathematik), Inversion
(Geometrie)
Englisch
Eric W. Weisstein (MathWorld)
Reflection
in Line, Rotation
Transform
Wikipedia
Reflection
(mathematics), Symmetry,
Reflection
symmetry,
Involution,
Inversive
geometry
MathsIsFun.com
symmetry,
Symmetry
Artist
Referenzen
top
(1) Martin Gardner: Geometrie mit Taxis, die Koepfe der
Hydra und andere mathematische Spielereien, Basel 1997
(2) Martin Gardner: Unsere gespiegelte Welt, Ullstein,
Frankfurt am Main, Wien 1982
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2008 Jürgen Köller
top |




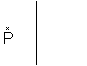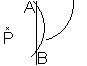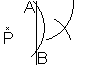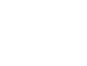

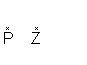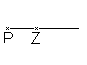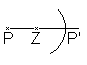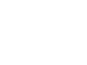





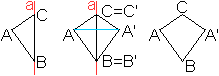
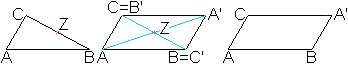



 ...
...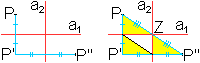 ...
...
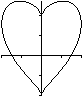
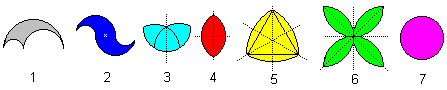

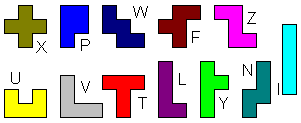

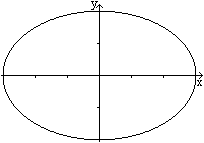
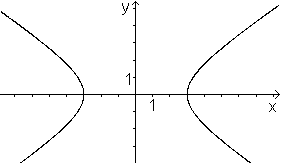


 ....
....