Apfelmännchen
Inhalt dieser Seite
Was ist ein Apfelmännchen?
Mathematischer Hintergrund
Programme und Videos		 Apfelmännchen im Internet
Referenzen
Verwandte Webseiten
Zur Hauptseite    "Mathematische Basteleien"

Was ist ein Apfelmännchen?
....... Die nebenstehende liegende schwarze Figur in der Mitte heißt nach ihrer Form Apfelmännchen oder nach ihrem Entdecker Mandelbrotmenge. 
Das Bild liegt in einem Koordinatensystem im Bereich -3 < x < 2 und -2 < y < 2. 
Die Computergrafik wird von farbigen Punkten gebildet. Die jeweilige Farbe wird aus den Koordinaten errechnet (Näheres siehe unten).
Das Besondere ist der gefranste Rand des Apfelmännchens. Er ist reich an Mustern. Greift man ein kleines Rechteck aus dem Randbezirk heraus und bestimmt nach den Formeln des Apfelmännchens farbige Punkte, so ergeben sich vielfältige, farbenreiche Muster, die sich je nach der Wahl der Randstelle stark unterscheiden. Muster wiederholen sich in der Umgebung einer Stelle, unterscheiden sich dann aber ein wenig. Man spricht von Selbstähnlichkeit.
...... Das Beispiel findet man im Bereich 

- 0.37465401 < x < - 0,37332411 und 

+0.659227668 < y < +0,66020767. 

Mathematischer Hintergrund top
Kurzfassung: Zu jedem Punkt wird eine Folge bestimmt. An der Folge wird eine Zahl abgelesen. Diese Zahl ist in einer Farbskala die Kennzahl einer Farbe, die der Punkt erhält.

Vom Punkt zur Folge
Setzt man komplexe Zahlen voraus, so heißt die Rekursionsformel der Folge zn+1=zn² + c. 
Dabei ist c=x1 + y1*i die Zahl, für die eine Farbe bestimmt werden soll.
z0=0 ist die Anfangszahl. 
Die Folge ist |zn|. 
Da viele mit komplexen Zahlen nicht vertraut sind, wähle ich den Weg über die reellen Zahlen.

Die folgenden Formeln werden für das Apfelmännchen verwendet. 
xn+1 = xn²-yn² + x1 und yn+1 = 2*xn*yn+ y1 und an+1 = SQRT(xn+1² + yn+1²) mit n = 0,1,2,3,... und x0=y0=0
(SQRT = Wurzel aus).

Die Rechnung wird am Beispiel des Punktes P1(x1|y1) = P1(-0.40|0.70) erklärt:

Ausgangspunkt ist für jeden Punkt der Nullpunkt N(0|0).
Es gilt x1 = x0²-y0² +x1 = 0-0+x1 = x1und y1= 2*x0*y0 + y1= 2*0*0+y1= y1, 
a1 = SQRT(x1² + y1²) = SQR[(-0.40)² + 0.70²] =0.81.
a1 ist die Entfernung des Punktes P1 vom Nullpunkt des Koordinatensystems.

Das zweite Glied der Folge errechnet sich aus den Koordinaten des Ausgangspunktes P1.
Dazu bestimmt man für einen zweiten Punkt zwei neue Koordinaten 
x2 = x1²-y1² +x1 =  (-0.40)² - 0.70² + (-0.40) = -0.73 und   y2= 2*x1*y1 + y1= 2*0*0+y1  = 2*(-0.40)*0.70+0.70 = 0.14. 
Daraus ergibt sich a2 = SQRT(x2² + y2²) = SQRT[(-0.73)² + 0.14²] = 0.74.

Das nächste dritte Glied der Folge errechnet sich aus den Koordinaten des vorhergehenden Punktes und des Ausgangspunktes.
Dazu berechnet man für einen dritten Punkt zwei neue Koordinaten 
x3 = x2²-y2² +x1  = (-0.73)² - 0.14² + (-0.40) = 0,11 und  y3= 2*x2*y2 + y1 = 2*(-0.73)*0.14+0.70 = 0.50. 
Daraus ergibt sich a3 = SQRT(x3² + y3²) = SQRT (0.11² + 0.50²) = 0.51.

Auf diese Weise erhält man für den Ausgangspunkt P1(-0.40|0.70) die Folge
 0.81, 0.74,  0.51,  1.0,  0.74,  1.1,  1.8,  2.4, ...

Fünf Punkte und ihre Folgen
Die folgende Tabelle hält die Folgen zu fünf Punkten (Beispiele) fest, die nach der gleichen Methode bestimmt worden sind.
.
.
Nr. der Folge:
1
2
3
4
5
6
7
8
9
10
11
12
13

.

 (0.20|0.20)

1.Folge:
0.23
0,34
0.35
0.33
0.30
0.30
0.31
0.32
0.32
0.31
0.31
0.31
...

. 

 (0.10|0.65)

2.Folge:
0.66 
0.84 
0.44 
0.57 
0.91 
0.83 
0.38 
0.70 
1.0
0,77
0.83
1.3 
2.1
...
.

 (-0.40|0.70) 

3.Folge:
0.81
0.74
0.51
1.0
0.74
1.1
1.8
2.4
4.9
24 
560 
320 000
...

.

 (0.50|1.30)

4. Folge:
1.4
2.8
6.5
43
1900 
3 500 000
...
.
.
.
.
.
.

.

 (2|2)

5. Folge:
3.6
16 
260 
68 000
...
.
.
.
.
.
.
.
.

.
Alle Zahlen werden auf 2 Ziffern gerundet. Das ist übersichtlicher.

Die erste Folge ist konvergent und strebt gegen 0.31. (Die Punkte mit konvergenten Folgen bilden das Apfelmännchen.)

Die übrigen Folgen sind offenbar divergent. Die Glieder der Folge gehen über alle Grenzen, allerdings unterschiedlich stark. 

Von der Folge zur Farbe
Überschreitet ein Glied der Folge die Zahl 2 (rot), so ist anzunehmen, dass die Folge über alle Grenzen geht. Das stimmt in etwa mit der Erfahrung überein. 
Wird nun 2 überschritten, so wird die Nummer des vorhergehenden Gliedes notiert. Sie wird Kennzahl in einer Farbskala. 
Diese Zahlen werden für die fünf Punkte oben in der folgenden Tabelle festgehalten: 
Punkt:
Farbe:		 (0.2|0.2)
schwarz		 (0.10|0.65)
12		 (-0.40|0.70)
7		 (0.50|1.30)
1		 (2|2)
0
Dem ersten Punkt mit der konvergenten Folge wird willkürlich die Farbe schwarz zugeordnet. Das führt zu einem schwarzen Apfelmännchen.
Vorausgesetzt, es steht  eine Farbskala mit 10 Farbstufen (0 bis 9) zur Verfügung. Ist eine Kennzahl größer als 9, so nimmt man die Zehnerreste. Beispiel: An Stelle von 12 in der zweiten Folge wählt man 2.

Jetzt können die Punkte gezeichnet werden. 

Computereinsatz
Der bisher dargestellte mathematische Hintergrund führt zu der Bearbeitung eines riesigen Zahlenmaterials. Für jeden Punkt muss eine Folge berechnet und ausgewertet werden. Das kann nur ein Computer bewältigen. 

Der Computer kann einen Fehler nicht vermeiden: Er kann nur endlich viele Glieder einer Folge berechnen. Untersucht der Computer zum Beispiel nur 50 Glieder, so kann es vorkommen, dass 2 nicht überschritten wird, dass aber trotzdem eine divergente Folge vorliegt. Der Fehler wird gemildert, wenn mehr Glieder berechnet werden. 
...... Je mehr Glieder der Folge berücksichtigt werden, desto mehr Einzelheiten zeigt die Grafik, wie das linke "animated Gif" zeigt. Die Anzahl steigt von 10 über 50, 100, 500 bis 1000.

Viele, die programmierten und an Computergrafik interessiert waren, haben sich in den 1980er Jahren und später am Apfelmännchen versucht. 
Es war  ein schönes Erlebnis, wenn ein relativ einfaches Programm zum ersten Mal, früher nach Stunden, das komplizierte Apfelmännchen hervorbrachte (C64-Nostalgie!).
Das ist die Umsetzung in die Programmiersprache Visul Basic V3.
...... Besonders schöne Bilder mit vielen Details findet man in den drei weißen Rechtecken bei ausreichender Vergrößerung. 
....... Immer wieder entdeckt man dunkelblaue Flecken, die sich nach Vergrößerung als neue Apfelmännchen entpuppen. Oft sitzt der Kopf schief. 
Fundstelle: 
0.435396403 < x < 0.451687191
0.367981352 < y < 0.380210061
Julia-Mengen
Die Julia-Mengen werden mit den gleichen Formeln wie oben berechnet, jedoch mit anderer Handhabung. 
In xn+1 = xn²-yn² +x0' und yn+1 = 2xn*yn+y0' und an+1 = SQR(xn+1²+yn+1²) wird für P(x0'|y0') ein bestimmter Punkt gewählt. 
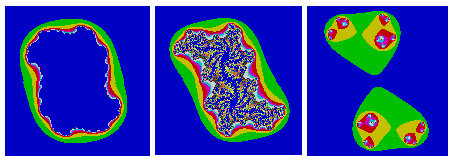
Unten sind drei Juliamengen dargestellt. Die Bilder gehören von links nach rechts zum Inneren, zum Randgebiet und zum Äußeren des Apfelmännchens. Im mittleren Bild stößt man auf detailreiche Muster mit großer Bildertiefe.

Programme und Videos    top
An dieser Stelle habe ich bis jetzt (Juli 2014) das über Jahre als Standardprogramm geltende Fractint für Windows (Winfract) empfohlen und besprochen, das aber unter Windows 7 nicht mehr läuft. Deshalb habe ich mich im Internet nach Ersatz umgesehen.

1
Nikko Strom: The Mandelbrot set (in Quite BASIC)
Wer zurückschauen möchte, dem sei dieses Programm empfohlen. Es zeigt nicht nur sein Listing, sondern man kann es auch online starten, indem man auf das Startdreieck oben links klickt. Dann wird das Apfelmännchen mit 100x100 Pixel gezeichnet. 
Das kommt gut heraus: Trotz der geringen Auflösung muss man mehr als eine halbe Stunde warten, bis das Bild vollendet ist.
2
M. Eric Carr: Mandelbrot Set Zoom    (Videoclip bei Youtube, 4:26 min)
Oben schreibe ich: Immer wieder entdeckt man dunkelblaue Flecken, die sich nach Vergrößerung als neue Apfelmännchen entpuppen.
Hier ist eine Demonstration.
3
teamfresh: Last Lights On - Mandelbrot fractal zoom to 6.066 e228 (2^760)    (Videoclip bei Vimeo, 13:45 min)
Eine atemberaubende Reise in die Tiefen des Apfelmännchens, ein Reichtum an Farben und Formen. 
Wer die fast 14 min durchhält, erlebt am Ende eine Überraschung, oder sie ist gar keine.
4
Harald Schmidt: Mandelbrot Applet
Dieser Link steht für die zahlreichen Java-Applets zur Mandelbrotmenge. 
Es stehen mehrere Programme bereit, mit deren Hilfe man sich an den Rändern des Apfelmännchens umsehen kann.
5 und 6
Georg Klein: Fractile plus
Tom Kerrigan: Fast Fractal
Wenn ich mit den Grafiken herumspielen möchte, benutze ich Apps auf dem IPad. 
Sie haben neben den brillanten Bildern und der leichten Handhabung auch die Möglichkeit, Bilder mit Hilfe von Koordinaten wieder zu finden und zu sichern. 

Fractile Plus

Fast Fractal
Ich möchte ihnen den Namen Sandalen geben.
Spiralen machen immer etwas her.

Fast Fractal   (-0,747162, -0,087584)


Fractile Plus   (-0,055394, +0,653645)

Apfelmännchen im Internet       top

Deutsch

Albert Kluge
Das fraktale Apfelmännchen (Mandelbrot-Menge) als Java-Applet

Alexander F.Walz
Die Mandelbrotmenge

Christian Gloor 
Fractals

Christian Symmank
Bilder der Mandelbrot Menge

Harald Schmidt
Mandelbrot Applet

Manfred Thole
Apfelmännchengalerie
Apfelmännchen, erzeugt in sechs Programmiersprachen: 
Java-Code, PostScript-Code, TeX/LaTeX-Code, C-Code, Mathematica-Notebook, Macsyma-Code

Thomas Hövel
wincig (Fraktalprogramm zum Herunterladen)

Wikipedia
Mandelbrot-Menge, Fractint


Englisch

Eric W. Weisstein
Mandelbrot Set

Jules Ruis
Centre for Fractal Design and Consultancy

M. Eric Carr 
Mandelbrot Zoom  (Video at youtube)

Michael Frame, Benoit Mandelbrot, and Nial Neger
Fractal Geometry

Nikko Strom
The Mandelbrot set (in Quite BASIC)

Robert Munafo
Mu-Ency - The Encyclopedia of the Mandelbrot Set

Wikipedia
Mandelbrot set, Fractint

Referenzen    top
T.Wegener, M.Peterson, B.Tyler, P.Branderhorst: Fraktale Welten für Windows, München 1993
James Gleick: Chaos - die Ordnung des Universums, Knaur München 1988

Verwandte Webseiten meiner Homepage (German only)       top

Langton-Ameise

 
 

Game of Life

Hüpfer

Feedback: Emailadresse auf meiner Hauptseite

Diese Seite ist auch in Englisch vorhanden.

URL meiner Homepage:
http://www.mathematische-basteleien.de/

©  2000, überarbeitet 7/2014, Jürgen Köller

top