|
Was ist eine vierstrahlige Figur?
... ... |
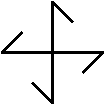Eine vierstrahlige Figur ist eine drehsymmetrische oder
kreissymmetrische Figur von der Ordnung vier.
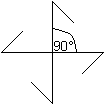
Das heißt, dass sie ein Drehzentrum hat und dass
sie bei jeder Vierteldrehung um dieses Zentrum in sich selbst übergeht. |
... ...
|
... ... |
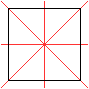
Auch das Quadrat ist vierstrahlig.
Bei ihm kommen noch vier Achsensymmetrien mit vier Achsen
hinzu. |
... ...
|
... |
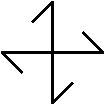Zu jeder vierstrahligen Figur gibt es ein Spiegelbild.
 |
Diese Seite hat den gleichen
Aufbau wie meine Seiten
Dreistrahlige Figuren,
Fünfstrahlige
Figuren, Sechsstrahlige Figuren, Siebenstrahlige
Figuren, Achtstrahlige
Figuren, Neunstrahlige Figuren.
Beispiele
vierstrahliger Figuren top
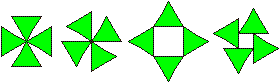
Vier gleichseitige Dreiecke
|
Vier 30-60-90-Dreiecke
|
Aus einem Quadrat mit 16 Dreiecken
|
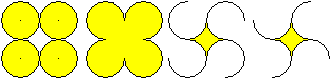
Vier Kreise
|
|
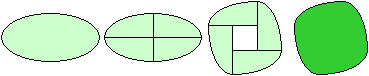
Von der Ellipse zur 4-Bogen-Linie
gefunden bei Steinhaus (2) auf Seite 84 |
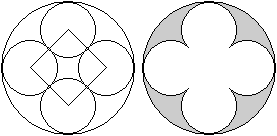
Maßwerk (Vierpass)
|
Autobahnkreuz
|
Windrose
|
Fast wie Feldlinienbilder
von Quadrupolen
Eine achtstrahlige Figur
ist auch vierstrahlig.
Vierstrahlige
Figuren mit einem Zeichenprogramm top
... |
Zeichne ein Quadrat und in ihm eine beliebige Figur.
|
... |
Drehe die Figur dreimal jeweils um 90°.
|
... |
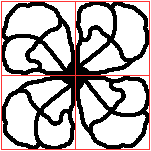Setze die vier Figuren zu einem 2x2-Quadrat zusammen.
|
... |
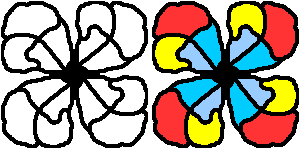Verschönere die Gesamtfigur.
|
Auf dem gleichen Wege entstanden
die drei Vierfachspiralen.
Erweiterung des Verfahrens auf Relationen
... ... |
 ... |
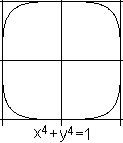
Durch die Gleichung x²+y²=1 wird bekanntlich
ein Kreis beschrieben. Er ist auch von der Gleichung her gesehen vierstrahlig,
denn die Gleichung ändert sich nicht, wenn man x durch -x, y durch
-y ersetzt und x und y vertauscht.
Will man neue Gleichungen entwickeln, muss man diese
Eigenschaften berücksichtigen.
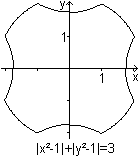
Mir fallen die Gleichungen zu einem gerundeten Quadrat
und zu einem Schild ein. -
Dieses ist ein weites Feld zum Experimentieren. |
Auf dieser Seite findet man
noch die Gleichungen (x²+y²)³=4x²y², (x²+y²-1)³+27x²y²=0
und (x2-a2)2+(y2-a2)2=b4.
Zykloiden top
Eine Herausforderung liegt darin, vierstrahlige Figuren
mit Hilfe von Formeln zu zeichnen.
Da bieten sich die Zykloiden
an.
Epizykloide
... ... |
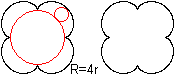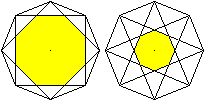
Man stelle sich vor, ein Kreis liege fest und ein zweiter
Kreis mit einem viermal so kleinen Radius rolle um einen großen Kreis
(Leitkreis) herum. Verfolgt man dabei einen Punkt auf der Kreislinie des
beweglichen Kreises, so beschreibt er eine geschlossene Linie mit vier
Einkerbungen. Diese Linie heißt Zykloide, genauer Epizykloide. Die
Figur ist vierstrahlig. |
Beschreibt man das Abrollen
durch Formeln, so ergibt sich:
Epizykloide, allgemein
 |
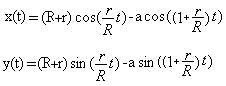Epizykloide für R=4r
x(t)=5r*cos(t/4)-a*cos(5t/4)
y(t)=5r*sin(t/4)-a*sin(5t/4)
|
Dabei sind R und r die Radien der Kreise. Die Variable a
gibt die Entfernung des Kurvenpunktes vom Mittelpunkt des beweglichen Kreises
an.
Es folgen Epizykloiden für
r=1 und verschiedene Parameter a.
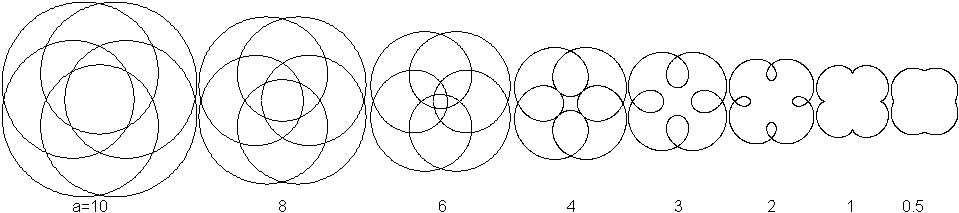Gezeichnet mit dem Freeware-Programm Winplot von Richard
Parris (URL unten)
Hypozykloide
... ...
|
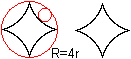Rollt man den kleinen Kreis innen ab, so entsteht eine
Figur mit vier Spitzen, die Hypozykloide. |
Beschreibt man das Abrollen
durch Formeln, so ergibt sich:
Hypozykloide, allgemein
 |
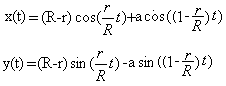Hypozykloide für R=4r
x(t)=3r*cos(t/4)+a*cos(3t/4)
y(t)=3r*sin(t/4)-a*sin(3t/4)
|
Dabei sind R und r die Radien der Kreise. Die Variable a
gibt die Entfernung des Kurvenpunktes vom Mittelpunkt des beweglichen Kreises
an.
Es folgen Hypozykloiden
für r=1 und verschiedene Parameter a.
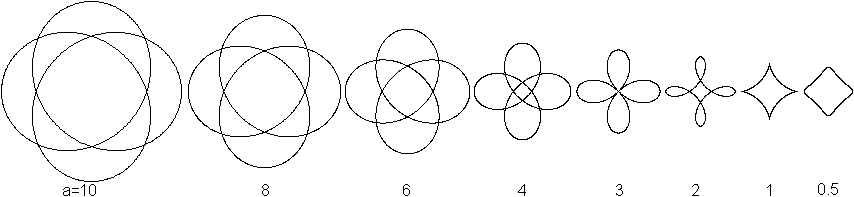Gezeichnet mit dem Freeware-Programm Winplot von Richard
Parris (URL unten)
Besondere Zykloiden
top
Von den oben vorgestellten Zykloiden mit R=4r sind drei
hervorzuheben.
Quadrifolium (Hypozykloide
a=3r)
... ..
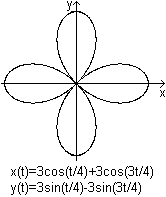.Es gilt 0<t<8*pi.
|
Im Polar-Koordinatensystem hat das Quadrifolium
eine
besonders einfache Darstellung:
r'(t)=a*sin(2t) [0<t<2*pi]. - Die Darstellung in
kartesischen Kordinaten ist (x²+y²)³=4x²y².
Der Flächeninhalt ist (1/2)*pi*a².
Die Länge kann nur angenähert angegeben werden,
da die Rechnung auf ein elliptisches Integral führt: L=9,69a.
Quelle: MathWorld (URL unten) |
Astroide
(Hypozykloide, a=r)
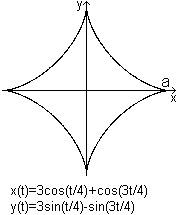
Es gilt 0<t<8*pi.
|
Die Parameterdarstellung lässt sich auch schreiben
als x=a*cos³(t) und y=a*sin³(t).
Die Darstellung in kartesischen Kordinaten ist
(x²+y²-1)³+27x²y²=0
Der Umfang ist L=6a und der Flächeninhalt (3/8)*pi*a².
Quelle: MathWorld (URL unten) |
Vierstrahlige
Epizykloide
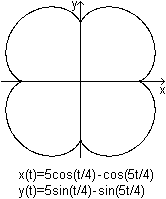
Vierstrahlige Körper
top
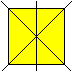
Zur Definition
|
|
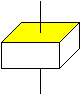
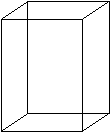
Verschiebt man eine Figur in Normalenrichtung, so entsteht
ein Prisma.
Ist die Figur vierstrahlig wie hier das gelbe Quadrat,
so ist auch das Prisma vierstrahlig.
Dabei wird der Drehpunkt durch eine Drehachse ersetzt.
Außerdem hat der Körper an Stelle vierer Symmetrieachsen
vier Symmetrieebenen. |
An diese Stelle passen drei
Bilder meiner Seite Quadratisches Prisma.
... und noch zwei Bilder
von der Seite
Himmel und Hölle
Vermischtes
Vierstrahliges aus der Natur
Schöllkraut
|
Raps
|
Flieder
|
Clematis
|
Karen's
Quilts
... |
Sandbild der Nordamerikanischen Ureinwohner,
fixiert mit Haarfestiger,
außerhalb des Kreises vierstrahlig,
hergestellt für Touristen,
kauften wir irgendwo in der Nähe des Grand Canyon,
USA. |
...
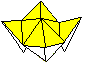
Vierstrahliger Stern von Shuzo Fujimoto,
gefaltet von Volker Sayn
|
Jakobsstern von Jakob Maier,
gefaltet von Volker Sayn
|
... ... |
Vierstrahlige Tulpe, gefaltet von Hannah.
Ein Anleitung von MsWellpappe findet man bei Youtube als
Origami Tulpe
(URL unten). |
... ... |
Eine Beschreibung, wie die Lilie zu falten ist, findet
man bei Youtube (URL unten).
Sie gehört zu Tavins Origami-Anleitungen. |
... ... |
Eine Fensterrosette der
neuromanischen evangelisch-lutherischen Erlöserkirche von 1891–1892
in Bad Salzuflen |
... |
Über 100 Jahre alte Wandfliese in einer Küche
in Speyer |
Vierstrahlige
Figuren im Internet top
Deutsch
Claas Hickl
Quattrofolium
(Entdecke die Welt der Kleeblätter)
MsWellpappe (Youtube)
Origami
Tulpe
Tavin (Youtube)
Origami
Blume
Wikipedia
Zykloide,
Epizykloiden,
Symmetrie
(Geometrie), Vierpass,
Radiärsymmetrie,
Drehgruppe,
Kreuz
(Symbol)
Englisch
EricW.Weisstein (MathWorld)
Epicycloid,
Hypocycloid,
Quadrifolium,
Astroid,
Rose
MacTutor History of Mathematics Archive
Hypocycloid,
Epicycloid,
Hypotrochoid,
Epitrochoid,
Astroid
Richard Parris (Freeware-Programme)
winplot
Wikipedia
Rotation,
Rotational
symmetry, Rotation
group, Rotation
(mathematics), Cross,
St.Brigid's
cross, Epicycloid,
Hypocycloid,
Astroid,
Quadrifolium
Xah Lee
Epicycloid
and Hypocycloid, Astroid
Französisch
Robert FERRÉOL
TRÈFLE
À QUATRE FEUILLES, ASTROÏDE,
Referenzen top
(1) I.N.Bronstein, K.A.Semendjajew: Taschenbuch der Mathematik,
Leipzig 1987
(2) Hugo Steinhaus: 100 Aufgaben, Leipzig-Jena-Berlin,
1968
Feedback: Emailadresse
auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2008 Jürgen Köller
top |
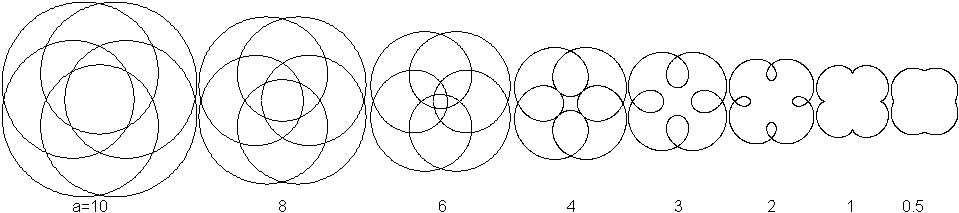
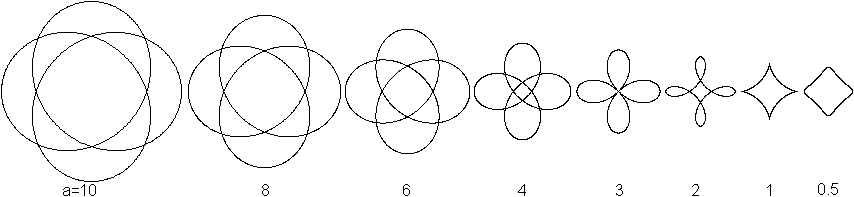
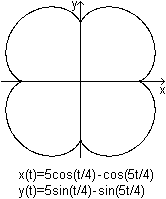
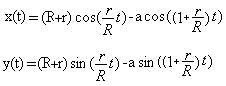
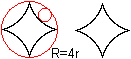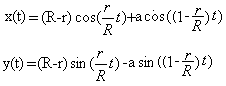
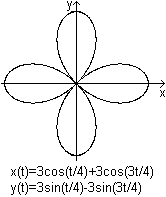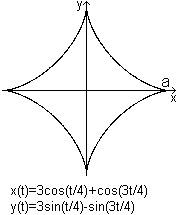
