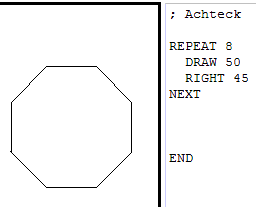
|
Was ist ein regelmäßiges Vieleck?
|
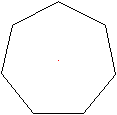
Das regelmäßige Vieleck hat
n Ecken
n gleich lange Seiten und
n gleich große Innenwinkel. (Die Variable
n steht für eine natürliche Zahl größer als 2.)
Stellvertretend für n-Ecke wird für die Zeichnungen meist
das Siebeneck gewählt. |
Das regelmäßige Vieleck heißt auch regelmäßiges
n-Eck oder in Anlehnung an die englische Bezeichnung reguläres Polygon.
Auf dieser Seite heißt es einfach Vieleck.
Die regelmäßigen Vielecke Dreieck
bis
Zwölfeck werden an anderer Stelle meiner Seite einzeln besprochen.
Zugang erhält man über die Hauptseite.
Größen des Vielecks
top
Winkel
... ...
|
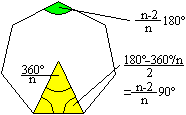
Ein regelmäßiges n-Eck wird durch das gelbe Bestimmungsdreieck
festgelegt.
Der Mittelpunktswinkel ist 360°/n.
Der Innenwinkel ist (n-2)/n*180°.
Die Summe aller Innenwinkel ist (n-2)*180°. |
Benennung der Diagonalen
... ... |
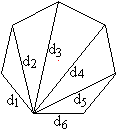Es ist praktisch, die Diagonalen des Vielecks (wie links beim Siebeneck)
mit di zu bezeichnen.
Man nimmt dann in Kauf, dass di auch eine Seite sein kann
und Diagonalen doppelt genannt werden.
Aber auf diese Weise werden die Formeln unten für die Diagonalen
einfach. |
Größen
... ... |
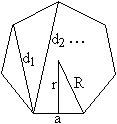Es gibt die Größen
Seite a, Radius r des Inkreises, Radius
R des Umkreises,
Diagonalen
di, Flächeninhalt
A und Umfang
U. |
Formeln
Ist die Seite a gegeben, so gilt
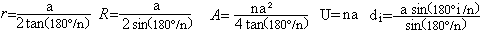
i=1,2,...n-1
Herleitung der Formeln
Radius r des Inkreises und Radius
R
des Umkreises
|
Es gilt sin(180/n)=(a/2)/R. Daraus folgt R=a/[2*sin(180/n)]
Es gilt tan(180/n)=(a/2)/r. Daraus folgt r=a/[2*tan(180/n)]. |
Diagonalen
|
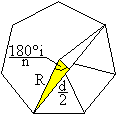
Es gilt sin(180i/n)=(di/2)/R oder di=2R*sin(180°/i).
Mit R=a/[2*sin(180/n)] ist di=[a*sin(180i/n)]/sin(180/n)
In der Zeichnung sind n=7 und i=3. |
Flächeninhalt
und Umfang
Der Flächeninhalt ist die n-fache Fläche des Bestimmungsdreiecks:
A=n*(a*r/2)=na²/[4*tan(180/n)].
Der Umfang ist U=na.
Ergänzung: Höhe
h
Hat das Vieleck eine ungerade Anzahl von Eckpunkten, so liegt die "Höhe"
h auf der Symmetrieachse des Vielecks.
|
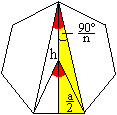
Es gilt tan(90°/n)=(a/2)/h oder h=a/[2tan(90°/n)]. |
Ist die Eckenzahl gerade, so ist die "Höhe" h=2r.
Anzahl der Diagonalen top
Lage der Diagonalen
... ...
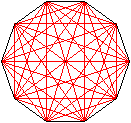Zehneck
|
... ...
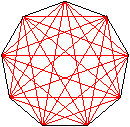Neuneck
|
Es ergeben sich z.B. für das Zehn- und Neuneck unterschiedliche
Bilder.
Ist die Eckenzahl gerade, so verlaufen die Diagonalen durch den Mittelpunkt.
Bei ungerader Eckenzahl ist die Mitte leer und die Diagonalen bilden
innen ein verkleinertes n-Eck. |
Anzahl aller Diagonalen
Gibt man die n Punkte des Vielecks vor, so kann man den ersten Punkt
mit n-1 Punkten verbinden.
Dann kann man den nächsten Punkt mit n-2 Punkten verbinden.
Den übernächsten Punkt verbindet man mit n-3 Punkten.
Diesen Prozess setzt man so lange fort, bis kein Punkt zum Verbinden
übrig bleibt.
Es gibt insgesamt (n-1)+(n-2)+(n-3)+...+3+2+1 Verbindungslinien. Das
kann man mit n(n-1)/2 zusammenfassen.
Man muss schließlich noch die n Strecken zwischen den Eckpunkten
abziehen.
Das führt zu n(n-1)/2-n=n(n-3)/2 Diagonalen.
Ergebnis: Das Vieleck hat n(n-3)/2 Diagonalen.
Anzahl der Diagonalen
unterschiedlicher Länge
.. ...
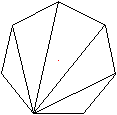n=7.
|
Man erhält die Anzahl der verschieden langen Diagonalen, wenn
man nur einen Punkt mit allen Eckpunkten verbindet.
Das ergibt n-1 Strecken.
Dann zieht man die beiden Seiten ab. Das ergibt n-3.
Schließlich halbiert man die Anzahl und erhält (n-3)/2.
Diese Überlegung gilt aber nur für Vielecke mit ungerader
Eckenzahl. |
... ...
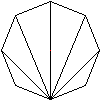n=8
|
Ist die Anzahl der Ecken des Vielecks gerade, so ist eine Diagonale
Symmetrieachse und tritt nur einmal auf. Deshalb ist die Anzahl gleich
(n-3+1)/2=(n-2)/2 bei geradem n. |
Ergebnis: Die Anzahl ist (n-3)/2, falls n
ungerade ist, und (n-2)/2, falls n gerade ist.
Symmetrie top
Jedes regelmäßige Vieleck ist
>punktsymmetrisch (Das Symmetriezentrum ist der Mittelpunkt.)
>n-fach drehsymmetrisch. (Bei einer Drehung um 360°/n kommt das
Vieleck wieder zur Deckung.)
>spiegelsymmetrisch (Es gibt n Symmetrieachsen.)
... ...
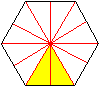Sechseck
|
Ist die Eckenzahl gerade, so verläuft eine Symmetrieachse immer
durch zwei Eckpunkte oder durch zwei Seitenmitten. |
... ...
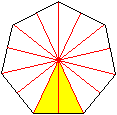Siebeneck
|
Ist die Eckenzahl ungerade, so verläuft eine Symmetrieachse immer
durch einen Eckpunkt und eine Seitenmitte. |
Aufteilung der Vielecke top
Aufteilung in Dreiecke
Es geht um das Problem, in wie viele Dreiecke die Diagonalen das Vieleck
zerlegen.
... ...
|
Für das Fünfeck zum Beispiel gibt es fünf Zerlegungen.
Dabei werden spiegelbildliche Zerlegungen als verschieden angesehen. |
Die Anzahl wird allgemein durch die Catalan-Zahlen
angegeben:
1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, ... (Sloane's A000108).
Es gilt:
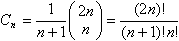
Aufteilung in Vielecke
Zeichnet man alle Diagonalen ein und beachtet auch ihre Schnittpunkte,
so ergibt sich das Problem der Aufteilung des regelmäßigen Vielecks
in verschiedene Vielecke.
... ... |
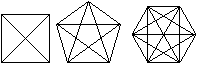Das sind beim Viereck 4, beim Fünfeck 11 und beim Sechseck 24
Vielecke, wie man durch Nachzählen bestätigen kann. |
Die ersten Glieder der Folge sind 1,4,11,24,50,80,154,220,375,444...
| Für ungerade n lautet die Formel allgemein: |
A(n)=(24 - 42n + 23n^2 - 6n^3 + n^4)/24 |
Für gerade n ist sie komplizierter. (siehe Sloane's A007678).
Alle Dreiecke im
Vieleck
|
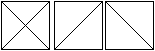
Das Viereck hat 4+2+2=8 Dreiecke. |
Eine Formel für die Anzahl aufzustellen ist schwierig, da man auch
gerade und ungerade Vielecke unterscheiden muss. Es gibt manchmal Mehrfachschnittpunkte.
Die ersten Glieder der Folge sind 1, 8, 35, 110, 287, 632,...
(Sloane's A006600).
Kreis und Vieleck top
... ... |
Ist der Kreis ein Vieleck?
Die Antwort ist nein. Das Vieleck müsste unendlich viele Ecken
haben, um zum Kreis zu werden. Aber Unendlich ist keine Anzahl. - Eine
Seite müsste die Länge 0 haben. Dann ist sie keine Seite mehr.
Man kann aber dem Kreis mit Vielecken beliebig nahe kommen und ihn
als Grenzfigur des Vielecks bezeichnen. Dabei lässt man die Zahl der
Eckpunkte über alle Grenzen gehen. |
Diese Betrachtung ist für die Kreisberechnung fruchtbar, denn die
Formeln des n-Ecks kann man für "n gegen Unendlich" für den Kreis
übernehmen.
Es gibt zwei Größen, die für den Kreis mit einem gegebenen
Radius r von Interesse sind, nämlich der Flächeninhalt A' und
der Umfang U'. Da beim Kreis A' und r² bzw. U' und 2r proportional
sind und der Proportionalitätsfaktor gleich Pi ist, läuft die
Kreisberechung auf die Bestimmung von Pi hinaus.
Kreis zwischen zwei
Vielecken
... ... |
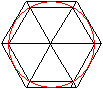In einer bekannten Methode wählt man zu einem Kreis mit dem Radius
r ein Sehnenvieleck und ein Tangentenvieleck und zwängt so den Kreis
ein. Man bestimmt für beliebiges n die Umfänge un
und Un der Vielecke und lässt n über alle Grenzen
gehen.
In der Zeichnung ist n=6. |
Intervallschachtelung
Für die Rechnung genügen Bestimmungsdreiecke.
|
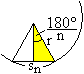
Sehnenvieleck:
Es gilt sin(180°/n)=sn/(2r) oder sn=2r*sin(180°/n)
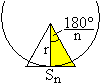
Tangentenvieleck:
Es gilt tan(180°/n)=Sn/(2r) oder Sn=2r*tan(180°/n) |
Die Umfänge gilt un=n*sn=2rn*sin(180°/n)
und Un=n*Sn=2rn*tan(180°/n).
Dann gilt die Intervallschachtelung
un<U'<Un
2rn*sin(180°/n) < U'< 2rn*tan(180°/n)
n*sin(180°/n) < U'/2r < n*tan(180°/n)
Mit Hilfe dieser Ungleichungskette kann man Pi beliebig genau bestimmen.
Zahlenbeispiel n=100: 100sin1,8°
<Pi <100tan1,8° oder 3,1410 < 3,1416< 3,1426.
Für die Flächeninhalte erhält
man die Intervallschachtelung
(1/2)n*sin(360°/n) < A'/r² < n*tan(180°/n).
Zahlenbeispiel n=100:
50*sin3,6° < Pi < 100*tan1,8° oder 3,1395 < Pi < 3,1426
Anmerkung:
In der Schule wird dieser Weg zur Bestimmung von Pi auch aus einem
praktischen Grund nicht beschritten. Trigonometrische Funktionen werden
erst nach der Kreisberechnung behandelt. Pi wird stattdessen durch Wurzelterme
erfasst.
Zu ihnen kann man auch über die Vielecke gelangen. Man untersucht
z.B. nacheinander das 4-Eck, 8-Eck, 16-Eck usw..
Die Wurzelterme berechnet man dann mit dem Taschenrechner.
In einem Bändchen von 1913 (1) fand ich aus Vor-Rechner-Zeiten
die unausgerechneten Terme für r=1
 ...
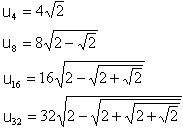Konstruierbarkeit der
Vielecke top
... ... |
... ...
|
Das gleichseitige Dreieck kann man mit Zirkel und Lineal zeichnen.
Das nennt man konstruieren.
Mit dem Dreieck sind auch das Sechseck, Zwölfeck, 24-Eck usw.
konstruierbar, denn man erhält sie nacheinander durch Winkelhalbieren. |
Es stellt sich die Frage, ob man alle regelmäßige
Vielecke konstruieren kann.
Das Problem ist gelöst, auch wenn man konkret nicht alle konstruierbaren
Vielecke kennt (*).
Nach Gauss weiß man, dass nur die p-Ecke (p ist eine Primzahl)
konstruierbar sind, bei denen es natürliche Zahlen k gibt, so dass
p=2^(2^k) +1 Primzahlen sind.
Das sind die n-Ecke mit der Eckenzahl 3, 5, 17, 257 und 65537. Weitere
Zahlen sind nicht bekannt (*).
Aus diesen " fermatschen Primzahlen" pi kann man durch
Produktbildung neue Zahlen bilden: p1p2p3...ps.
Beachtet man noch, dass jede dieser Zahlen wegen der Halbierungen oben
Ausgangszahl einer Folge von neuen Zahlen sein kann, erhält man mit
2m p1p2p3...ps eine
allgemeine Darstellung. Vielecke mit dieser Eckenzahl sind also konstruierbar.
Konkret sind das die Zahlen
3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51,
60, 64, 68, 80, 85, 96, ... (Sloane's A003401).
Die n-Ecke mit der Eckenzahl 7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25,...sind
nicht konstruierbar.
Es gibt für sie Näherungskonstruktionen.
Eine Maximaleigenschaft top
... ... |
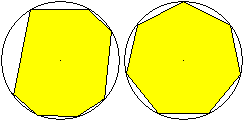Für regelmäßige Vielecke gilt der Satz:
Unter allen n-Ecken, die einem Kreis einbeschrieben sind, hat das regelmäßige
den größten Flächeninhalt.
Der Satz ist einleuchtend, der Beweis ist aber nicht ganz einfach.
Einen gedanklich und textlich sorgfältig dargestellten Beweis
findet man bei Rademacher/Toeplitz (4) auf den Seiten 9 bis 14. |
Vielecke im Internet
top
Deutsch
Holger Ullmann
ORNAMENTIK IM VIER-VIERTEL-TAKT
Michael Holzapfel
Regelmäßige
Vielecke
Ursula Damm
Meine geometrischen
Muster aus regulären Polygonen
Werner Brefeld
Regelmäßiges
Vieleck und Zerschneiden
Wikipedia
Polygon
Englisch
1728 Software Systems
Regular Polygon Calculator
Eric S Rowland
Regular
Polygons
Dr.Math (The Math Forum)
Eric W. Weisstein (MathWorld)
CatalanNumber
ConstructiblePolygon
PolygonDiagonal
Polygons
RegularPolygon
N. J. A. Sloane (On-Line Encyclopedia of Integer Sequences)
Integer
Sequences
Paul A. Gusmorino
Paul's Page of
Pi
Peter Steinbach
Golden
Fields: A Case for the Heptagon
Steven E. Sommars - Tim Sommars
The
Number of Triangles Formed by Intersecting Diagonals of a Regular Polygon
Silvio Levy
Regular
Polygons
Wikipedia
Polygon
Japanisch
Referenzen top
(1) Eugen Beutel: Die Quadratur des Kreises, Leipzig Berlin 1913 /
1942
(2) W.Lietzmann: Altes und Neues vom Kreis, Leipzig Berlin 1935
(3) Jean-Paul Delahaye: Pi die Story, Birkhäuser Verlag, Basel
Boston Berlin 1999
(4) Rademacher-Toeplitz: Von Zahlen und Figuren, Springer, Berlin,
Heidelberg, New York1968 (Nachdruck von 1930)
Feedback: Emailadresse auf
meiner Hauptseite
URL meiner
Homepage:
http://www.mathematische-basteleien.de/
©
2005 Jürgen Köller
top |
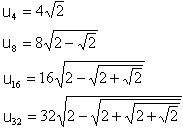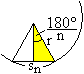
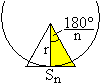
