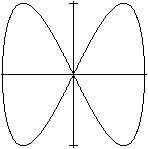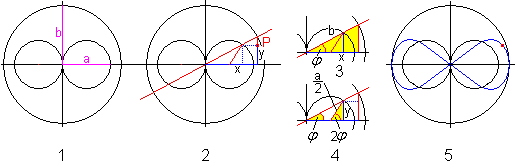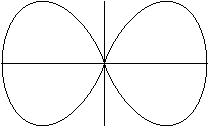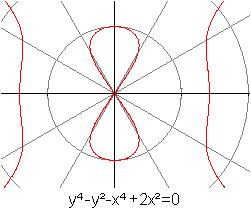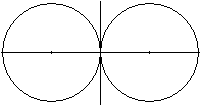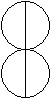Acht-Kurve

Achtkurve

Inhalt dieser Seite

Was ist die Achtkurve?
Schreibweisen der Acht
Acht aus Bögen und Strecken
Lemniskate von Bernoulli

Lemniskate von Gerono, Lissajous-Figur
Weitere Achtkurven
Räumliche Acht
Achtkurven im Internet
.

Zur Hauptseite "Mathematische Basteleien"

Was ist die Achtkurve?

...... Die Achtkurve ist eine Kurve in Form einer Acht.
Die Acht hat wohl von den zehn Ziffern wegen der Punkt- und Achsensymmetrie das schönste Aussehen.
......

Es gibt keinen einheitlichen Namen für diese Kurve. Man könnte sie auch Achterkurve, achtförmige Kurve oder achtförmige Linie nennen. Der Name Achtkurve steht in Analogie zu dem der Herzkurve.
Im Englischen findet man die Namen Eight Curve, Eight Shaped Curve und Figure (of) Eight Curve. Über diese Wörter gelangt man bei einer Suchmachine wie google.com zu Seiten über die Acht.

Die liegende Acht ist bekannt geworden als Zeichen für "Unendlich".

Schreibweisen der Acht top

...... Schreibt man die Ziffer 8, so beginnen die meisten oben in der Mitte.
Rechtshänder zeichnen zuerst die obere geschlossene Linie als Linkskurve, Linkshänder als Rechtskurve.
Diese Arten des Schreibens wünscht auch der "Palm", bei dem ein OCR-Programm die Acht dann erkennt.

Obwohl die Figur der Acht wohldefiniert ist, kann sie unterschiedliches Aussehen haben.
Als Beispiel folgen Darstellungen der Acht aus Zeichensätzen unter Windows.

Die Acht ganz rechts ist in Sütterlin-Schrift geschrieben.

Acht aus Bögen und Strecken top
Die Acht besteht im einfachen Falle aus zwei Kreisen und den Tangentenabschnitten der inneren gemeinsamen Tangenten.
Konstruktion:

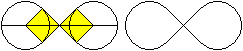...... > Zeichne zwei Quadrate Ecke an Ecke (gelb).
> Zeichne je einen Kreis um die äußeren Eckpunkt mit dem Radius der Seitenlänge eines Quadrats.
>Kennzeichne die Acht.

Es sei der Radius r des Kreises gegeben.
Die Figur setzt sich aus zwei Dreiviertelkreisen und zwei Quadraten zusammen.
Länge der Achtkurve
Die Länge oder der Umfang ist U=4r+2(3/4)(2*pi*r)=(4+3*pi)r.
Flächeninhalt der Achtkurve
A=2[(3/4)*pi*r²]+2r²=(3*pi+4)r²/2

Verallgemeinerung
In einem allgemeineren Fall stehen die Tangenten nicht unbedingt aufeinander senkrecht.

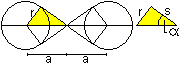r ist der Radius, 2a der Abstand der Mittelpunkte, 2*alpha der Winkel zwischen den Tangenten.

Angenommen, der Radius r und der Winkel alpha sind gegeben.
Länge der Achtkurve
Die Länge setzt sich aus zwei Kreisbögen und vier Tangentenabschnitten zusammen: U=2U'+4s.
U' ist die Länge der Kreislinie mit dem Umfangswinkel 180°+2alpha.
Es gilt die Proportion U':(2*pi*r)=(180°+2alpha):360°. Daraus folgt U'=pi*r(90°+alpha)/90°.
Nach der Definion des Tangens ist tan(alpha)=r/s oder s=r/tan(alpha).
Eingesetzt U=pi*r(90°+alpha)/45°+4r/tan(alpha).

Flächeninhalt der Achtkurve
Der Flächeninhalt setzt sich aus zwei Kreisausschnitten und vier rechtwinkligen Dreiecken zusammen: A=2A'+4A''
Für einen Kreisausschnitt gilt A':pi*r²=(180°+2alpha):360° oder A'=pi*r²(90+alpha)/90
Für ein Dreieck gilt A''=rs/2=(1/2)r²/tan(alpha).
A=2A'+4A''=[(90°+alpha)/90°*pi+2/tan(alpha)]r²

Ist a=2r, so entarten die Tangentenabschnitte zu einem Punkt und die Acht zu einem Doppelkreis.

Lemniskate von Bernoulli top
Definition

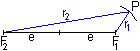...... Für die Lemniskate gilt r₁r₂=e².
In Worte: Die Punkte, deren Produkt der Entfernungen von den festen Punkten F₁ und F₂ gleich dem Quadrat der halben Entfernung der Punkte ist, liegen auf einer Kurve, der Lemniskate.

Polargleichung

...

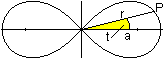
Die Lemniskate hat die Polargleichung r² = 2e²cos(2t) oder r=e*sqrt[2cos(t)].

Ist t=0, so ist r=sqrt(2)*e=a. Dann ist r=a*sqrt[cos(2t)].

Herleitung der Formel

...

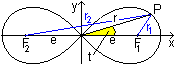
Nach dem Kosinussatz ist r₁²=r²+e²-2re*cos(t) und r₂²=r²+e²-2re*cos(180°-t) oder r₂²=r²+e²+2re*cos(t).
Daraus folgt r₁²r₂²=(r²+e²)²-4r²e²cos²(t).
Wegen r₁r₂=e² ist (r²+e²)²-4r²e²cos²(t)=e⁴oder mit e ungleich 0 ist r²=4e²cos²(t)-2e².
Mit cos(2t)=2cos²(t)-1 ist r²=2e²cos(2t) qed.

Herleitung der Koordinatengleichung

...

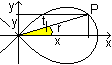
Es gilt allgemein r²=x²+y² und cos(t)=x/r.
Setzt man diese Terme in r²=a²cos²(t)-a² ein, ergibt sich (x²+y²)²-a²(x²-y²)=0.

Ergebnis: Die Koordinatengleichung ist (x²+y²)²-a²(x²-y²)=0.

Herleitung der Parametergleichung
Es gilt allgemein x=r*cos(t) und y=r*sin(t).
Hier gilt speziell r=a*sqrt[cos(2t)]
Daraus folgen die Parametergleichungen x=a*sqrt[cos(2t)]*cos(t) und y=a*sqrt[cos(2t)]*sin(t).

Erste Ableitung
y'=dy/dx=(dy/dt)/(dx/dt)=y'(t)/x'(t).
x(t)=a*sqrt[cos(2t)]*cos(t) führt zu x'(t)= -a*sin(2t)*cos(t)/sqrt[cos(2t)]-a*sin(t)*sqrt[cos(2t)]= -a*sin(3t)/sqrt[cos(2t)]
y(t)=a*sqrt[cos(2t)]*sin(t) führt zu y'(t)= -a*sin(2t)*sin(t)/sqrt[cos(2t)]+a*cos(t)*sqrt[cos(2t)]= a*cos(3t)/sqrt[cos(2t)]
y'=y'(t)/x'(t)= -cot(3t)

Besondere Punkte
Wegen der Punktsymmetrie der Lemniskate kann man sich auf den ersten Quadranten beschränken.

...

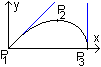In P₁ist ein Wende- und Knotenpunkt mit der Steigung 1 bzw. -1.
P₂ ist ein Hochpunkt mit r=30° und den Koordinaten x₂=sqrt(6)/4 und y₂=sqrt(2)/4.
P₃ ist ein Punkt mit x₃=a und einer vertikalen Tangente.

Die Aussagen zu den drei Punkten können mit Gleichungen oben begründet werden.

Flächeninhalt
Die Lemniskate schließt zwei Flächenstücke ein. Für den Flächeninhalt im 1.Quadranten gilt

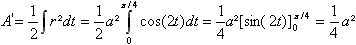Da die Lemniskate punktsymmetrisch ist, gilt für die gesamte Fläche A=a².

Länge
Bei der Bestimmung der Länge der Lemniskate gelangt man zur Formel

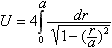Das Integral ist als elliptisches Integral nur näherungsweise zu lösen.
Für a=1 ergibt sich U=5,244...
Näheres findet man z.B. bei MathWorld unter "Lemniscate Function".

Die Lemniskate als Spezialfall der Cassinischen Kurven

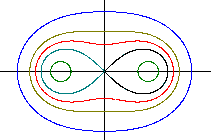Die Cassinischen Kurven werden durch die Gleichung (x²+y²)² - 2e² (x²-y²) - a⁴ + e⁴=0 beschrieben.
Die nebenstehenden Cassinischen Kurven entstehen, wenn man e=6 festhält und für a die Werte 10 (blau), 8.5 (grau), 7 ( rot), 6 (schwarz) und 4 (grün) einsetzt.

Für a=e=6 ergibt sich die Lemniskate.

Etwas mehr über Cassinische Kurven findet man auf meiner Seite Eilinien.

Lemniskate von Gerono, Lissajous-Figur top

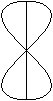
Lemniskate von Gerono
(Eight Curve)

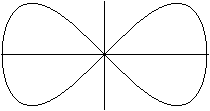
x⁴-b²x²+b²y²=0 mit b=1 Eine Lissajous-Figur

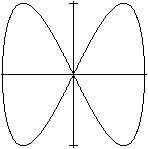
x=cos(t) /\ y=sin(2t)
oder 4x⁴-4x²+y²=0

Beide Kurven gehören zur Kurvenschar a²x⁴-a²b²x²+b⁴y²=0 oder besser geschrieben als (x/b)⁴ – (x/b)² + (y/a)² = 0.
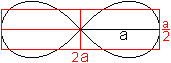
Einmal ist a=b(=1) und zum anderen b=1 und (a=2).

Die Erzeugung von Kurven dieser Art kann man sich folgendermaßen vorstellen:

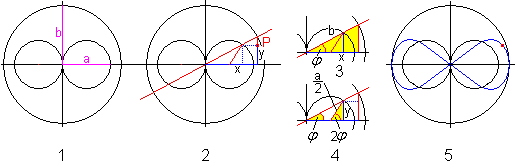
1 Gegeben ist ein Kreis mit dem Radius b und darin zentral zwei sich berührende Kreise mit dem Durchmesser a. Sie liegen in einem Koordinatensystem.
2 Eine Ursprungsgerade soll sich um den Nullpunkt des Koordinatensystems um 360° drehen. Der Drehwinkel sei phi.
Dabei wird ein Punkt verfolgt, der durch die Schnittpunkte der Geraden mit dem b-Kreis und a-Kreis bestimmt wird.
Seine x-Koordinate ist der x-Wert des Schnittpunktes mit dem b-Kreis.
Seine y-Koordinate ist der y-Wert des Schnittpunktes mit dem a-Kreis.
3 Für den x-Wert gilt cos(phi)=x/b
4 Für den y-Wert gilt sin(2*phi)=y/(a/2). (2*phi ist der Mittelpunktswinkel zu phi.)
Aus den Gleichungen unter 3 und 4 folgt die Koordinatengleichung a²x⁴-a²b²x²+b⁴y²=0.
Dabei verwendet man sin(2*phi)=2sin(phi)cos(phi)
5 Die Kurve hat die Parameter a=5 und b=6.

Weitere Achtkurven top

Kurve von Watt

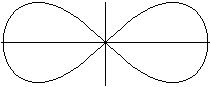
r²=b²-[a*sin(t)(c²-a²cos²(t))]²
mit a=b=1, c²=2 xxx

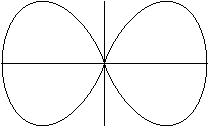
y²=x²*ln(a²/x²) mit a=1 Quelle (3)

Hippopede

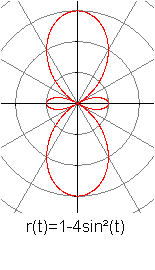
Devil's Curve

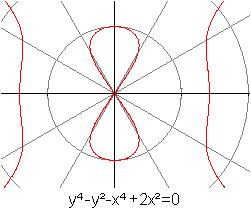
Eine Nephroide

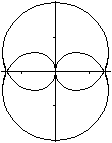
x=cos(t)-cos(3t).
y=sin(t)-sin(3t)

Doppelkreis

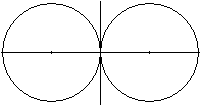
r=abs[cos(t)] oder
(x+1)²+y²=R² /\ (x-1)²+y²=R²
mit R=1

Doppeleier meiner Seite Eilinien:

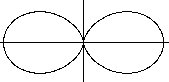
r(t)=cos²t

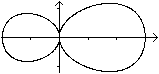
x⁴+2x²y²+4y⁴-x³-6x²-xy²=0

Noch eine Acht: (x/3)²*((x/3)²-1)+0.25*(abs(y))²=0

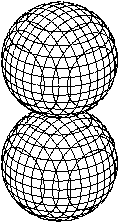
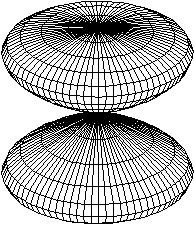
Räumliche Acht top
Ein rotierender Doppelkreis erzeugt eine räumliche Acht.

Eine rotierende Lemniskate erzeugt eine räumliche Acht.

Achtkurven im Internet top

Deutsch

Prof Dr. Dörte Haftendorn
Boothsche Lemniskaten

Gernot Zimmermann
Das Analemma-Projekt

Hans-Jürgen Caspar (Mathroid)
Kurvenverwandtschaft bei der konformen Abbildung w=1/z

Ingmar Rubin (ZUM)
Der optimale Schwimmring

J. Frank (Werner-von-Siemens-Gymnasium Berlin)
Kurven in Parameterdarstellung (Beispiel: Lemniskate)

Wikpedia
Lemniskate, Hippopede, Unendlichkeit, Acht, Achtknoten, Achterbahn

Englisch

Gustavo Gordillo
A Collection of Famous Plane Curves

Eric W. Weisstein (MathWorld)
Butterfly Curve, Devil's Curve, Dumbell Curve, Eight Curve, Eight Surface, Lemniscate, Lemniscate Function,
Toric Section, Viviani's Curve

Ivars Peterson
Strange Orbits

Jan Wassenaar (2dcurves)
besace (a Lissajous curve), Cassinian oval, hippopede (curve of Booth), Watt's curve

JOC/EFR/BS (Famous curves index)
Devil's Curve, Figure Eight Curve, Lemniscate of Bernoulli, Spiric Sections

Wikipedia
Lemniscate of Bernoulli, Lemniscate of Booth, Lemniscate of Gerono, Infinity, Eight, Figure of Eight Knot

W. Volk
Münze/Coin (Zeugnisse über Mathematiker - Monuments on Mathematicians)

Xah Lee (Famous Plane Curves)
Lemniscate of Gerono, Lemniscate of Bernoulli, Nephroid

Französisch
Robert Ferreol (mathcurve.com)
LEMNISCATE DE BERNOULLI, LEMNISCATE DE BOOTH, LEMNISCATE DE GERONO, SPIRIQUE DE PERSÉE,
COURBE DE WATT

Referenzen top
(1) Heinz Nickel (Hrsg.): Algebra und Geometrie für Ingenieur- und Fachschulen, Verlag Harry Deutsch, Frankfurt/M und Zürich, 1966
(2) W. Leupold (Hrsg.): Analysis für Ingenieur- und Fachschulen, Verlag Harry Deutsch, Frankfurt/M und Zürich, 1966
(3) Richard Doerfling: Mathematik für Ingenieure und Techniker, München 1965

Feedback: Emailadresse auf meiner Hauptseite

top
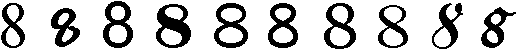
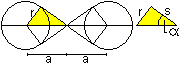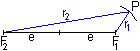