|
Was ist ein Pentagramm?
... |
Ein Pentagramm ist ein regelmäßiger Stern
mit fünf Zacken. |
Entstehung
...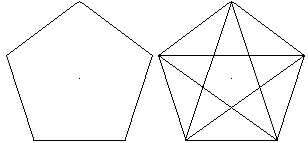 ... ... |
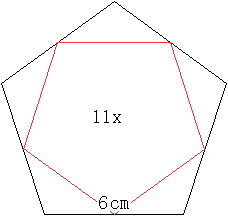
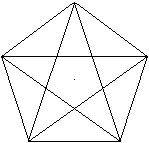
Der Stern entsteht, indem man in einem regelmäßigen
Fünfeck jeden zweiten Eckpunkt miteinander verbindet.
Er liegt zwischen einem großen und kleinen Fünfeck. |
... ... ... |
Der Stern entsteht auch, indem man in einem regelmäßigen
Fünfeck die Diagonalen einzeichnet. |
...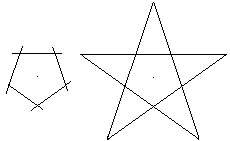 ... ... |
Der Stern entsteht auch, wenn man die Seiten eines regelmäßigen
Fünfecks bis zu den Schnittpunkten verlängert. |
.. . . |
Das Pentagramm entsteht auch, wenn man auf die Seiten
eines regelmäßigen Fünfecks fünf gleichschenklige
Dreiecke mit einem Winkel von 36° an der Spitze stellt. |
Unregelmäßiges
Pentagramm
...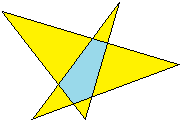 ... ... |
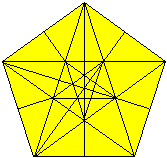
Wenn man vom Wort her kommt, muss man auch den nebenstehenden
Stern als Pentagramm bezeichnen, denn Pentagramm heißt "mit fünf
Strichen".
Im Sprachgebrauch ist ein Pentagramm das regelmäßige. |
Fünfzackstern
... ... ... |
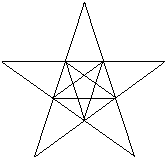
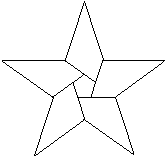
Ein allgemeinerer fünfzackiger Stern entsteht, wenn
man auf ein konvexes Fünfeck beliebige Dreiecke stellt.
Diesen Stern sollte man nicht mehr als Pentagramm bezeichnen.
Er besteht nicht aus fünf, sondern aus 15 Strichen oder Strecken.
Er heißt Fünfstern, fünfzackiger Stern,
Fünfzackstern oder Fünfeckstern. |
Einordnung
...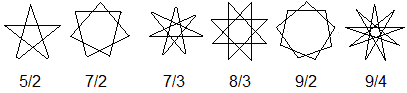 ... ... |
Das Pentagramm gehört zu den Polygrammen,
die durch Brüche gekennzeichnet werden. |
Die erste Zahl gibt die Anzahl der
Eckpunkte des erzeugenden Vielecks an, die zweite die "Sprungweite" beim
Verbinden der Eckpunkte.
Erweiterung
Die beiden unregelmäßigen Sterne sind nahe
liegende Verallgemeinerungen des regelmäßigen Sterns.
Sie sind aber keine "mathematischen" Erweiterungen.
Mehr dazu auf meiner Seite Polygramm.
Spielereien top
Zwei Figuren
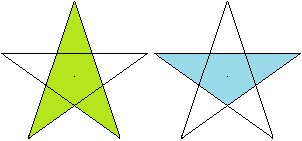 |
Das Pentagramm besteht aus einem konkaven Viereck und
einem gleichschenkligen Dreieck. |
Buchstabe
A
...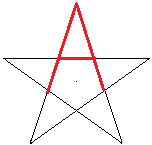 ... ... |
Im Pentagramm steckt fünfmal der große Buchstabe
A. |
Keltischer
Knoten
... ... ... |
Zeichnet man die Seiten des Pentagramms dicker und dann
abwechselnd Brücken und Unterführungen, so entsteht ein geflochtener
Stern. |
Drachenvierecke
...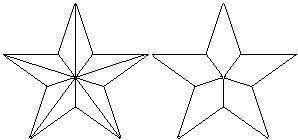 ... ... |
Zeichnet man die Diagonalen des Pentagramms, so gelangt
man zu fünf Drachenvierecken. |
Sterne
im Fünfeck
Überschlagene
regelmäßige Fünfecke
...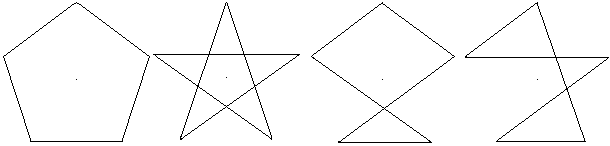 ... ... |
Das Pentagramm kann man auch als ein regelmäßiges
Fünfeck ansehen, bei dem die fünf Eckpunkte durch Linien verbunden
werden, die sich überschneiden.
Es gibt durch die fünf Eckpunkte zwei weitere Figuren. |
Die Figuren heißen auch unikursale Pentagone. Sie sind
Hamiltonkreise, da Punkte durch eine geschlossene Linie verbunden werden.
Fertige
Pentagramme
... ... ... |
Zu Windows 10 gehört das Zeichenprogramm MSPaint.
Es bietet die Möglichkeit, fertige Pentagramme aufzurufen.
 |
... ... ... |
Es gibt die Unicode-Zeichen Pentagramm (U+26E4)
und Umgekehrtes Pentagramm (U+26E7). |
Zehnecksterne
...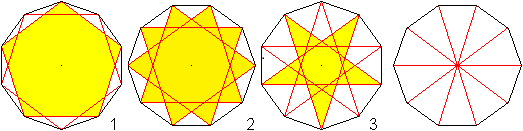 ... ... |
Im Zehneck liegen drei Sterne.
Im Zehneck 3 besteht er aus zwei Pentagrammen................ |
Figuren
zählen
Kepler-Poinsot-Körper
...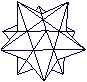 |
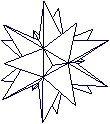 |
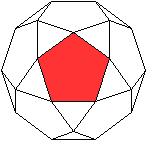
Das Kleine Sterndodekaeder und das Große
Sterndodekaeder werden von je 12 Pentagrammen erzeugt.
Näheres erfährt man auf meiner Seite Kepler-Poinsot-Körper. |
...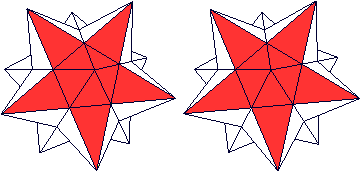 |
Hier wird beim Großen Dodekaeder ein Pentagramm
betont.
Auf ihm steht eine fünfseitige gerade Pyramide. |
Winkel top
...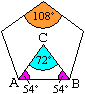 ... ... |
Im Grunddreieck ABC des regelmäßigen Fünfecks
ist der Mittelpunktswinkel gleich 360°/5 = 72°.
Damit sind die beiden Basiswinkel gleich 54°. Der
Innenwinkel des Fünfecks ist dann gleich 108°. |
...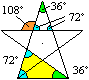 ... ... |
Nimmt man an, dass das Fünfeck im Inneren des Pentagramms
auch regelmäßig ist, so ist der gekennzeichnete Scheitelwinkel
gleich 108°. Der Zacken ist ein gleichschenkliges 72-36-72-Dreieck.
Unten liegt schräg ein zweites kleineres 72-36-72-Dreieck. |
Goldener
Schnitt top
...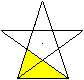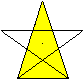 ... ... |
Die beiden gelben Dreiecke sind wegen entsprechender,
gleicher Winkel einander ähnlich.
So gelangt man im Folgenden zu Formeln. |
...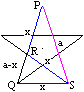 ... ... |
Wegen der Ähnlichkeit der gelben Dreiecke gilt PQ:QS=QS:QR
oder a:x=x:(a-x).
Diese Gleichung kann auf die Strecke PQ und den Teilungspunkt
R bezogen werden. Die ganze Strecke verhält sich zum größeren
Abschnitt wie dieser größere Abschnitt zum kleineren. Man kann
auch sagen: Der größere Abschnitt ist die mittlere Proportionale
des ganzen und des kleineren Abschnitts, in Formeln x=sqrt[a(a-x)]. |
Man sagt: In einem regelmäßigen
Fünfeck schneiden sich die Diagonalen im Goldenen Schnitt. Das Teilungsverhältnis
kann aus der Proportion s:a=a:(s-a) berechnet werden. Nach der Produktengleichung
ist a(a-x)=x². Dann ist x²+ax-a²=0. Löst man diese
quadratische Gleichung auf, so ergibt sich als positive Lösung x =[1/2*sqr(5)-1/2]a.
Das ist ungefähr 0,62a.
Ein Kapitel meiner Webseite Goldener
Schnitt.
Umkreis
und Inkreis top
... |
Der Umkreis des Pentagramms ist der Umkreis des umfassenden
Fünfecks.
Der Inkreis des Pentagramms ist der Inkreis des umfassenden
Fünfecks.
|
...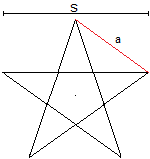 |
Das Pentagramm sei durch die Seitenlänge a des umfassenden
Fünfecks gegeben. |
Für
die Berechnung der Radien benötigt man man die Gleichungen
sin(36°) = (1/4)sqrt[10-2sqrt(5)]
oder besser 1/sin(36°) = csc(36°)= (1/5)sqrt[50+10sqrt(5)] und
cot(36°) = (1/5)sqrt[25+10sqrt(5)].
Radius des Umkreises R
... |
Man kann in einem gleichschenkligen Dreieck ein rechtwinkliges
finden und
sin(alpha) = (a/2)/R ablesen.
Dann ist R = (1/2)csc(36°)*a = (1/10)sqrt[50+10sqrt(5)]*a
oder angenähert R = 0,85a. |
Radius
des Inkreises r
... |
Im gleichen Dreieck kann man cot(alpha) = r/(a/2) ablesen.
Dann ist r = (1/2)cot(36°)*a = (1/10)sqrt[25+10sqrt(5)]*a
oder angenähert r = 0,69a. |
Ergebnis: R = (1/10)sqrt[50+10sqrt(5)]*a
und r = (1/10)sqrt[25+10sqrt(5)]*a
Flächeninhalt top
... ... ... |
Der Stern sei wieder durch die Seite a des umfassenden
Fünfecks gegeben. |
...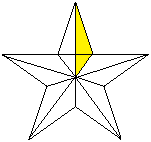 ... ... |
Es ist günstig, das Pentagramm in zehn kongruente
Dreiecke so aufzuteilen, dass man den Radius des Umkreises verwenden kann. |
...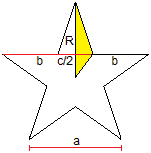 ... ... |
Das gelbe Dreieck hat den Flächeninhalt A' = (1/2)R(c/2),
das Pentagramm dann A = 10A' = (5/2)Rc.
Dabei sind R die Grundseite und c/2 die Höhe des
gelben Dreiecks. |
Der Radius des Umkreises
ist, wie oben gezeigt, R = (1/10)sqrt[50+10sqrt(5)]a.
Vor c bestimmt man über
den Goldenen Schnitt die Länge des Teilabschnittes b.
Es gilt (a+b):a = a:b.
Das führt zu (a+b)b = a² oder b²+ab-a²=0
oder b2 = -(1/2)a+(1/2)sqrt(5)a.
Aus a-b =c folgt c = (1/2)[3-sqrt(5)]a.
Es gilt A = (5/2)Rc
= (5/2)*(1/10)(1/2)sqrt[50+10sqrt(5)]a*[3-sqrt(5)]*a
= (1/8)sqrt[50+10sqrt(5)]*[sqrt[14-6sqrt(5)]a²
= (1/8)sqrt[400-160sqrt(5)]a²
= (1/2)sqrt[25-10sqrt(5)]a²
Ergebnis: Der Flächeninhalt des Pentagramms ist
A
= (1/2)sqrt[25-10sqrt(5)]a².
Nachbemerkung
...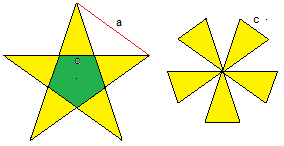 ... ... |
Es ist naheliegend, den Flächeninhalt des Pentagramms
mit Hilfe des inneren Fünfecks und der fünf Zacken zu bestimmen.
Dabei könnte man vielleicht verwenden, dass zehn gelbe Dreiecke ein
regelmäßiges Zehneck bilden.
Doch die Rechnung ist "a little bit lengthy". |
Eine Folge
von Pentagrammen top
 |
Man erhält eine Folge von Pentagrammen,
indem man das Pentagramm 1 vorgibt
und in dessen inneren Fünfeck das Pentagramm 2 einzeichnet.
Das dritte Pentagramm liegt im inneren Fünfeck des
Pentagramms 2.
Das kann man fortsetzen. |
Rechnungen dazu:
Seiten der umfassenden Fünfecke
der Sterne.
Oben steht die Formel c = (1/2)[3-sqrt(5)]a. Nach
dem goldenen Schnitt ist phi = (1/2)[-1+sqrt(5)] oder phi² = (1/2)[3-sqrt(5)].
Damit gilt c = (phi²)a. Für den dritten Stern
gilt dann d = (phi²)c.
So kann sukzessiv jedes Glied der Folge aus dem vorherigen
bestimmt werden.
Für Folgen ist es günstiger,
die Glieder der Folge zu nummerieren.
x(1) = a,
x(2) = (phi^2)a oder angenähert x(2) = 0,382a
x(3) = (phi^4)a = 0,146a
x(4) = (phi^6)a = 0,0556a
...
Das allgemeine Glied ist x(n) = [phi^(2n-2)]a.
Das ist eine konvergente geometrische Folge mit dem Quotienten
phi^2.
Der Grenzwert der zugehörigen Reihe ist [1/(1-q)]a
= [1/(1-phi^2)]a oder angenähert 1,618a.
Das ist die Summe der Längen aller Seiten.
Flächeninhalte
Der Flächeninhalt des ersten
Pentagramms wird oben bestimmt mit A(1) = (1/2)sqrt[25-10sqrt(5)]a².
Zur Abkürzung sei k =(1/2)sqrt[25-10sqrt(5)]. Somit
ist A(1) = ka²
 |
Das führt zur Folge
ka², k(phi^4)a², k(phi^8)a², ...
mit dem allgemeinen Glied A(n) = k[phi^(4n-4)]a². |
Es gilt A(1) : A(2)
:
A(3) = 1: [(phi^4] : [(phi^8)] oder angenähert
A(1) : A(2) : A(3) = 1 : 0,15 : 0,021 = 100
:
15
:
2,1.
Daten eines
Zackendreiecks top
...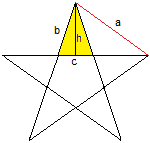 ... ... |
Der Stern sei wieder durch die Seite a des umfassenden
Fünfecks gegeben.
Das Zackendreieck oder kurz die Zacke ist gleichschenklig,
Die Grundseite ist c, die Schenkel b.
Der Winkel an der Spitze ist 36° groß. |
Grundseite
und Schenkel einer Zacke
 |
Die Seiten einer Zacke sind oben bereits bestimmt.
Es gilt c = (1/2)[3-sqrt(5)]a oder gerundet c
= 0,382a.
Es gilt b = (1/2)[-1+sqrt(5)]a oder gerundet b
= 0,618a. |
Höhe
einer Zacke
... ... ... |
Der Winkel an der Spitze ist 36° groß.
Es gilt im halben Zackendreieck cos(18°) = h/b ober
h = b cos(18°). |
Man weiß cos(18°) = (1/4)sqrt[10+2sqrt(5)]
Dann ist h = b cos(18°) = (1/8)[-1+sqrt(5)][10+2sqrt(5)]a
= (1/8)sqrt[6-2sqrt(5)][10+2sqrt(5)]a
= (1/8)sqrt[40-8sqrt(5)]a = (1/4)sqrt[10-2sqrt(5)]a
oder
gerundet h = 0,588a.
Flächeninhalt
einer Zacke
Es gilt A(Zacke) = (1/2)ch = (1/2)(1/2)[(3-sqrt(5)](1/4)sqrt[10-2sqrt(5)]a²
= (1/16)sqrt[200-88sqrt(5)]a² = (1/8)sqrt[50-22sqrt(5)]a²
oder gerundet A(Zacke) = 0,112a².
Besondere
Fünfzacksterne top
...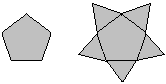 |
Es geht in diesem Kapitel um Sterne aus regelmäßigen
Fünfecken, auf dessen Seiten gleichseitige Dreiecke stehen. |
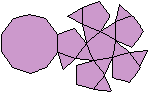
Drei
Johnson-Körper
Eine Reihe von Körpern enthalten diese Sterne,
wobei die Zacken hochgeklappt sind.
Da wird man bei den Johnson-Körpern fündig.
1 Fünfeckkuppel
J02
...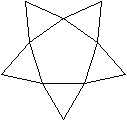 ... ... |
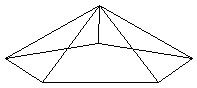 ... ... |
Die Spitzen der Zacken werden hochgeklappt bis sie sich
berühren. Der Körper ist eine fünfseitige gerade Pyramide
und heißt als Johnson-Körper Fünfeckkuppel. |
Körper, die nur von regelmäßigen Vielecken
begrenzt werden, heißen m.E. Johnson-Körper.
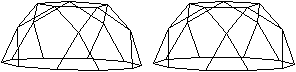
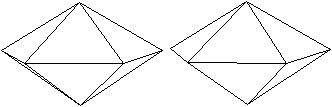
2 Fünfeckrotunde
J06
Der Körper entsteht, wenn man ein Ikosidodekaeder
halbiert.
Die beiden nebeneinander liegenden Bilder ermöglichen
eine dreidimensionale Ansicht.
3 Pentagonale
Bipyramide J13
Der Körper wird nur von Dreiecken begrenzt und zählt
deshalb auch zu den Deltaedern.
Man könnte diese Reihe
von Johnson-Körpern fortsetzen. Davon kann man sich auf meiner Seite
Johnson-Körper
überzeugen.
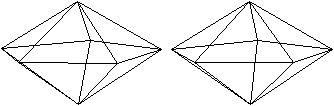
Pentagonales
Antiprisma
...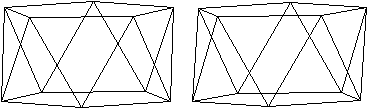 ... ... |
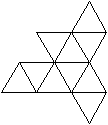
Für die Bildung des Pentagonalen Antiprismas
benötigt man zwei Sterrne. |
... ... ... |
Schaut man auf das Antiprisma, so erkennt man, dass die
Zacken beim Hochklappen nicht ganz 90° erreichen. |
Sternzahlen
top
...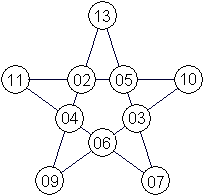 |
Mehr über den magischen Stern auf meiner Seite Magische
Quadrate.................................................... |
...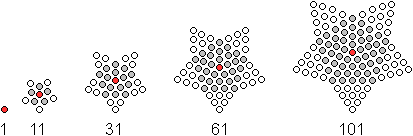 .. .. |
Bei dieser Folge von Sternen werden die Kreise gezählt.
Mehr auf meiner Seite Figurierte
Zahlen |
Fünfzacksterne
aus Perlen top
... ... ... |
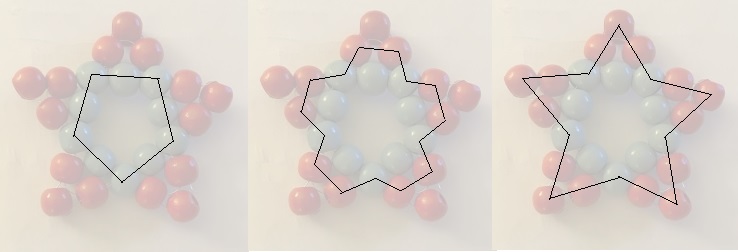
Man benötigt für diesen Stern 25 Holzperlen
und einen etwa 100 cm langen Draht mit einem Durchmesser von etwa 0,3 mm.
(Ich habe beides bei Kik gekauft.)
Der Draht wird zu drei geschlossenen Ringen gebogen und
nimmt dabei Perlen auf..
Für den ersten Umlauf zieht man 10 Perlen auf den
Draht auf und verdrillt die beiden Enden, wobei man das eine Ende kurz
wählt. Es entsteht der blaue Ring.
Beim zweiten Umlauf kommt 5x ein rotes Perlenpaar dazu.
Bei dritten Umlauf werden fünf rote Einzelperlen
hinzugefügt, die die Spitze einer Zacke bilden.
Zum Schluss werden die Drahtenden verdrillt und abgeschnitten. |
Bild
dazu
...
Schnell gemacht
...
Sternpyramide top
...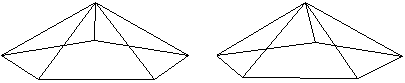 ... ... |
Vorgegeben ist eine gerade fünfseitige Pyramide.
Sie ist der Johnsonkörper J7. |
Man
zeichnet in das Fünfeck das Pentagramm.
...
Dann verbindet man die Eckpunkte
des Pentagramms mit der Spitze der Pyramide und löscht die Seiten
des Fünfecks. Es ist die "Sternpyramide" mit einem Pentagramm als
Grundfläche entstanden.
...
...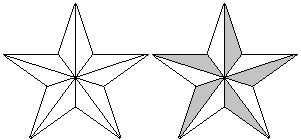 ... ... |
Zeichnet man in ein Pentagramm die Diagonalen ein und
färbt jedes zweites Dreieck grau, so hat man den Eindruck, die Sternpyramide
von oben zu sehen. |
... ... ... |
Diese einfache Faltfigur aus einem Fünfeck ist keine
Sternpyramide. Die Grundfläche ist nicht eben. |
Verschiedenes top
Lucky Star
Freihand
zeichnen
... ... ... |
Man kann das Pentagramm oder Sterne mit 5, 7, 9 , ...
Zacken mit etwas Übung aus freier Hand zeichnen, ohne den Stift abzusetzen. |
Fadenspiel
Pentagramm
aus fünf Trinkhalmen
...
Eine Anleitung findet man im Internet mit "Stern aus
Strohhalmen".
Gefalteteter
Fünfeckstern
 |
Kunstvolle fünfstrahlige Faltarbeit..................................................................... |
Mehr auf meiner Seite Fünfstrahlige
Figuren
Fünfeck-Leuchte
Text zu den Bildern findet man auf meiner Seite Pentagondodekaeder.
Drudenfuß
top
Das Pentagramm heißt auch Drudenfuß oder
Hexenstern.
Das ist ein Hinweis auf eine außerhalb der Mathematik
liegende Thematik.
Mein Beitrag wäre: Ich habe in den fünfziger
Jahren auf einem Bauernhof an der Tür des kombinierten Pferde-/Kuhstalls
ein Pentagramm gesehen. Es sollte Krankheiten vom Vieh fernhalten.
Es folgt noch ein Hinweis
auf meine Seite Regelmäßiges Fünfeck.
Pentagramm im
Internet top
Deutsch
alamy
Fünfeckstern
deschdanja
5
zackiger Stern
Online-Rechner
Pentagramm
Sternpyramide
Wikipedia
Pentagramm,
Pentagon,
Stern
(Geometrie), Roter
Stern, Davidstern,
Hippasos
von Metapont,
Youtube
schaeresteipapier
Origami
Stern,
Youtube
G Torbz Crafty Channel
3D STAR
MAKING WITH PAPER 3D STAR MAKING WITH PAPER
Englisch
Eric W. Weisstein (World of Mathematics)
Pentagram,
Pentagrammic
Prism, Pentagrammic
Antiprism,
Pentagrammic
Dipyramid, Star
Polygon
Harvey Heinz
Order
5 Magic Stars
Wikipedia
Pentagram,
Pentagon,
Pentagonal
pyramid,
Pentagrammic
prism, Pentagrammic
antiprism,
Pentagrammic
crossed-antiprism,Star
polygon, Red star,
Star
of David, Hippasus
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
11/2023 Jürgen Köller
top |






 ...
... ...
... .
. ...
... ...
... ...
...
 ...
... ...
... ...
...



 ...
... ...
...
 ...
... ...
...



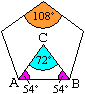 ...
...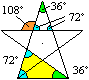 ...
... ...
...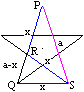 ...
...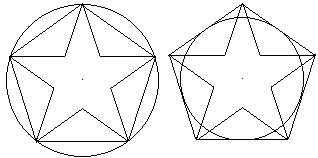



 ...
... ...
... ...
...
 ...
...
 ...
... ...
...
 ...............
...............
 ...
... ...
... 
 ..
.. ...
... ...
... ...
... ...
...
 ...
...