|
Was ist ein regelmäßiges
Zehneck?
|
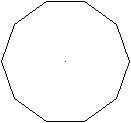
Das regelmäßige Zehneck ist ein Vieleck mit
zehn gleich langen Seiten und
zehn gleich großen Innenwinkeln. |
Das Zehneck heißt auch Dekagon.
Im Englischen ist wohl der Name Decagon üblich.
Man findet auch 10 sided figure.
Das erwähne ich hier, um die Suche im Internet zu
erleichtern.
Auf dieser Seite heißt
das regelmäßige Zehneck meist einfach Zehneck.
Größen
des Zehnecks
top
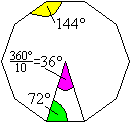
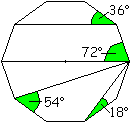
Winkel im Zehneck
Formeln
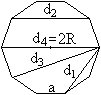
Seite und Diagonalen
|
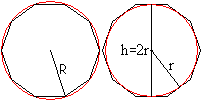
Radius des Umkreises, Radius des Inkreises, Höhe
|
Ist die Seite a gegeben, so lassen sich daraus
der Radius r des Inkreises, der Radius
R des Umkreises, die
Diagonalen
d1,d2
,
d3
und
d4,
die Höhe h, der Flächeninhalt
A und der Umfang
U
errechnen.
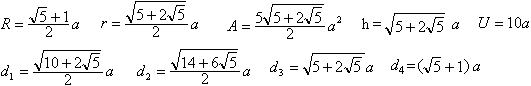
Herleitung der Formeln
Radius des Umkreises
... ... ...
|
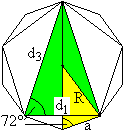
Im Zehneck liegt ein Fünfeck. Auf meiner Seite
regelmäßiges Fünfeck steht, dass die
Diagonale und die Seite im Verhältnis des Goldenen
Schnittes stehen.
Das heißt hier d3:d1=(1/2)[(sqrt(5)+1]:1.
Es gilt die Proportion d3:d1
= R:a wegen der Ähnlichkeit der farbigen Dreiecke.
Also ist auch R:a=(1/2)[sqrt(5)+1] oder R=(1/2)[sqrt(5)+1]a. |
Es gilt also der bekannte
Satz: Im Zehneck stehen Umkreisradius und Seite im Verhältnis des
Goldenen Schnittes.
Deshalb heißt das gelbe Dreieck auch das "Goldene
Dreieck".
Radius
des Inkreises
.. .... ....
|
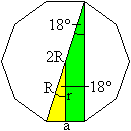
Es gilt cos18°=r/R oder r=R*cos18°.
Nach der Zeichnung ist sin18°=a/(2R) ab.
Mit R=(1/2)[sqrt(5)+1]a ergibt sich sin18°=(1/4)[sqrt(5)-1].
Aus sin²18°+cos218°=1 ergibt
sich cos18°=(1/4)sqrt[10+2sqrt(5)]. |
Dann ist nach längerer Rechnung
r=R*cos18°=(1/2)[sqrt(5)+1]a *(1/4)sqrt[10+2sqrt(5)]=(1/2)sqrt[5+2sqrt(5)]a.
Erste Diagonale
..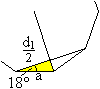 .... ....
|
Es gilt cos18°=d1/2a oder d1=2a*cos18°.
Es ist cos18°=(1/4)sqrt[10+2sqrt(5)].
Dann ist d1=(1/2)[10+2sqrt(5)]a. |
Zweite Diagonale
 ...... ......
|
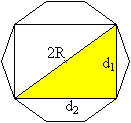
Nach dem Satz des Pythagoras ist d2²+d1²=(2R)².
Dann ist d2=sqrt(4R²-d1²)
mit R=(1/2)[sqrt(5)+1]a und d1=(1/2)[10+2sqrt(5)]a.
Nach längerer Rechnung ist d2=(1/2)sqrt[14+6sqrt(5)]a. |
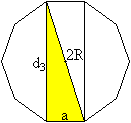
Dritte Diagonale
... ... ...
|
Nach dem Satz des Pythagoras gilt (2R)²=d3²+a².
Dann ist d3=sqrt(4R²-a²) mit R=(1/2)[sqrt(5)+1]a.
Nach längerer Rechnung ist d3=sqrt[5+2sqrt(5)]a. |
Vierte Diagonale und Höhe
Es gilt d4 =2R und
h=2r.
Flächeninhalt und Umfang
A=10*[(1/2)ar] = 10[(1/2)a*sqrt[5+2sqrt(5)]/2*a=(5/2)a²(sqrt[5+2sqrt(5)]
U=10a
Noch
eine Formel
... ... ...
|
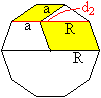
Im Zehneck liegen zwei Parallelogramme, so dass man die
Beziehung d2=R+a erkennt. |
Konstruktion
eines Zehnecks top
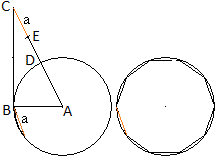 |
Zeichne einen Kreis um A mit dem Radius R=AB. Er wird
der Umkreis des Zehnecks werden.
Zeichne die Senkrechte durch B zu AB und trage die Strecke
BC =2R ab.
Verbinde die Punkte A und C und nenne den Schnittpunkt
mit dem Kreis Punkt D.
Halbiere die Strecke CD und nenne den Halbierungspunkt
E.
Trage die Strecke a=CE zehnmal auf dem Kreis ab.
Du erhälst so das Zehneck. |
Begründung
Die Konstruktion benutzt die Formel R=(1/2)[sqrt(5)+1]a
bzw. a=(1/2)[sqrt(5)-1)]R.
Das Dreieck ABC ist ein rechtwinkliges Dreieck mit den
Seiten R, 2R und nach dem Satz des Pythagoras sqrt(5)R.
Die Strecke CD=AC-AD ist sqrt(5)R-R. Die Strecke
CE ist dann a=(1/2)[sqrt(5)R-R] = (1/2)[sqrt(5)-1)]R.
Diagonalen top
Alle Diagonalen
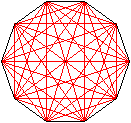
|
Das Zehneck hat 35 Diagonalen. |
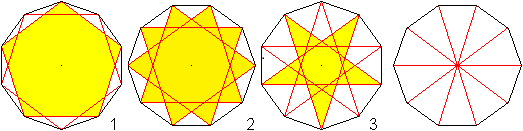 >Zehn Diagonalen verbinden jeden zweiten, zehn jeden dritten
und zehn jeden vierten Eckpunkt.
>Zehn Diagonalen verbinden jeden zweiten, zehn jeden dritten
und zehn jeden vierten Eckpunkt.
>Fünf Diagonalen verlaufen durch den Mittelpunkt.
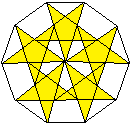
>Die Diagonalen bilden drei voneinander unabhängige
Sterne, die Dekagramme.
>Der linke Stern 1 besteht aus zwei regelmäßigen
Fünfecken,
die mit der Drehung eines Sterns um 36° zur Deckung gebracht werden
können.
>Der mittlere Stern 2 kann in einem Zug gezeichnet werden.
>Der mittlere Stern 3 besteht aus zwei Pentagrammen,
die mit der Drehung eines Sterns um 36° zur Deckung gebracht werden
können.
>Die Winkel an den Spitzen der Sterne sind 108°,
72° und 54°.
Figuren
aus Diagonalen oder Diagonalenabschnitten

Zehnecke bei Körpern
Zwei archimedische Körper
top
Pentagondodekaeder
...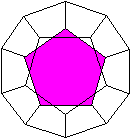 ... ... |
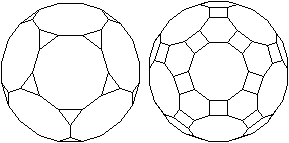
Liegt bei einer Parallelprojektion des Pentagondodekaeders
eine Fünfeckfläche parallel zur Zeichenebene, so ist der Umriss
ein Zehneck |
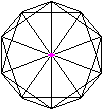
Ikosaeder
... ... ...
|
Steht bei einer Parallelprojektion des Ikosaeders
eine Ecke oben oder - anders ausgedrückt - eine Raumdiagonale senkrecht
zur Zeichenebene, so ist der Umriss ein Zehneck |
Regelmäßiges
Zehneck im Internet top
Deutsch
Christoph Pöppe (Spektrum der Wissenschaft)
Pflastern
Sie mit!
DER SPIEGEL
Quasi-Kristalle:
Die faszinierende Geometrie des Orient
Wikipedia
Zehneck
Englisch
Eric W. Weisstein (mathworld)
Decagon,
Decagram,
Golden
Triangle
Greg Frederickson
Frederickson's
Pentagram (Folding a Decagon to a Pentagram)
John Page
Decagon
Kate Jones (Kadon Enterprises, Inc.)
Tilings
and Designs (DEKA-MOSAIKTM, DEKA-STARTM,KITE-MOSAIKTM)
Kenneth James Michael MacLean
THE
DECAGON
Wikipedia
Decagon
Referenzen top
(1)W.Gellert (Hrsg.): Kleine Enzyklopädie Mathematik,
Leipzig 1986
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2005 Jürgen Köller
top |
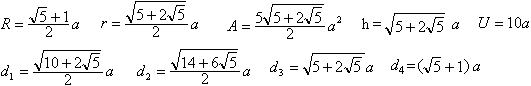



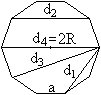
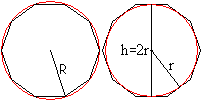
 ...
... ....
....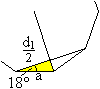 ....
.... ......
...... ...
... ...
...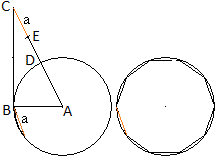


 ...
... ...
... ...
...