| .
Was ist ein Nonagramm?
... |
 |
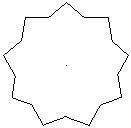
Ein Nonagramm ist ein regelmäßiger Stern mit
neun Zacken. |
.. .... |
 ... |
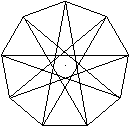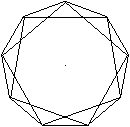
Es gibt zwei Möglichkeiten, die Eckpunkte eines
Neunecks so zu verbinden, dass ein Stern aus einer geschlossenen
Linie entsteht. Man überspringt beim Verbinden einen oder drei Punkte. |
Zusammengesetztes
Nonagramm
... |
Es gibt noch einen dritten regelmäßigen Stern
im Neuneck. |
... |
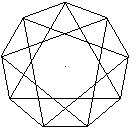Er entsteht, indem man in einem Neuneck beim Verbinden
der Punkte zwei überspringt. |
... ... |
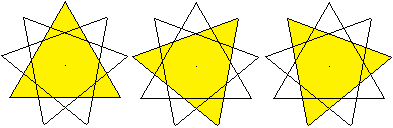Dieser Stern besteht aus drei Dreiecken.
Deshalb ist dieser Stern im Gegensatz zu den beiden oben
ein zusammengesetztes Nonagramm. Er zählt deshalb nicht zu den Nonagrammen
(ohne Zusatz). |
Unregelmäßiges
Nonagramm
... ... |
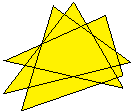Wenn man vom Wort her kommt, müsste man auch den
nebenstehenden Stern als Nonagramm bezeichnen, denn Nonagramm heißt
"mit neun Strichen". |
Neunzackstern
... ... |
Ein allgemeiner neunzackiger Stern entsteht, wenn man
auf ein konvexes Neuneck beliebige Dreiecke stellt. Diesen Stern sollte
man nicht mehr als Nonagramm bezeichnen. Er besteht nicht aus sechs, sondern
aus 27 Strichen oder Strecken.
Er heißt neuneckiger Stern, Neunzackstern, Neuneckstern
oder Neunstern. |
Einordnung
... ... |
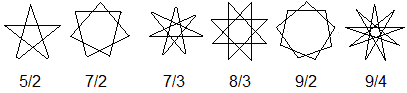Das Nonagramm gehört zu den Polygrammen,
die durch Brüche gekennzeichnet werden. |
Die erste Zahl gibt die Anzahl der
Eckpunkte des erzeugenden Vielecks an, die zweite die "Sprungweite" beim
Verbinden der Eckpunkte.
 |
Der Stern 9/3 ist ein zusammengesetztes
Polygramm und besteht aus drei gleichseitigen Dreiecken. |
Formeln
top
In diesem Kapitel geht es um Formeln für die drei
Nonagramme, den 9/2-Stern, den 9/3-Stern und den 9/4-Stern.
An einem Heptagramm werden
bekannte Größen eines Polygramms angezeigt.
... |
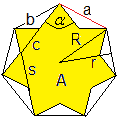alpha - Winkel an der Spitze
s - Seitenlänge
c - Grundseite einer Zacke
b - Schenkel einer Zacke |
R - Radius des Umkreises
r - Radius des Inkreises
A - Flächeninhalt des Sterns
a - Seitenlänge des umfassenden Fünfecks |
Wenn die Seite a des umfassenden
Vielecks (Polygons) gegeben ist, so gelten für den p/q-Stern die folgenden
Formeln.
Winkel an der Spitze alpha
Seitenlänge s
Grundseite einer Zacke c
Schenkel einer Zacke b
Radius des Umkreises R
Radius des Inkreises r
Flächeninhalt des Sterns A |
alpha = [(p-2q)/p]*180°
s = a*sin(180°q/p)/sin(180°/p)
c = a*{sin[(p-2q)/2p]*180°}/{cos[(q-1)/p]*180°}
b = (a/2)/{cos[(q-1)/p]*180°}
R = (a/2)/sin(180°/p)
r = (a/2)/tan(180°/p)
A = (1/4) {1/tan(180°/p)-tan[(q-1)/p*180°]}pa² |
Für den 9/2-Stern, also für p=9 und q=2, gilt:
| Winkel an der Spitze alpha = [(p-2q)/p]*180° = (5/9)*180°
= 100°
Seitenlänge s = a*sin(180°q/p)/sin(180°/p)
= a*(sin 40°/9)/(sin 20°)
Grundseite einer Zacke c = a*{sin[(p-2q)/2p]*180°}/{cos[(q-1)/p]*180°}
= a*sin 50°/cos 20°
Schenkel einer Zacke b = (a/2)/{cos[(q-1)/p]*180°}
= (a/2)/cos 20°
Radius des Umkreises R = (a/2)/sin(180°/p)
= (a/2)/sin 20°
Radius des Inkreises r = (a/2)/tan(180°/p) =
(a/2/tan 20°
Flächeninhalt A = (1/4) {1/tan(180°/p)-tan[(q-1)/p*180°]}pa²
= (9/4)(1/tan 20°-tan 20°) |
.Gerundete Werte.
.
.s = 1,87a ...........
.
.c = 0,81a
.
.b = 0,53a
.
.R = 1,46a
.
.r = 1,38a
.
.A = 5.36a² |
Für den 9/3-Stern, also für p=9 und q=3 gilt:
| Winkel an der Spitze alpha = [(p-2q)/p]*180° = (1/3)*180°
= 60°
Seitenlänge s = a*sin(180°q/p)/sin(180°/p)
= a*sin 60°/sin 20°
Grundseite einer Zacke c = a*{sin[(p-2q)/2p]*180°}/{cos[(q-1)/p]*180°}
= a*sin 30°/cos 40°
Schenkel einer Zacke b = (a/2)/{cos[(q-1)/p]*180°}
= (a/2)/(cos 40°)
Radius des Umkreises R = (a/2)/sin(180°/p)
= (a/2)/sin 20°
Radius des Inkreises r = r = (a/2)/tan(180°/p)
= (a/2)/tan 20°
Flächeninhalt A = (1/4) {1/tan(180°/p)-tan[(q-1)/p*180°]}pa²
= (9/4)(1/tan 20°-tan 40°) |
.Gerundete Werte.
.
.s = 2,53a ...........
.
.c = 0,65a
.
.b = 0,65a
.
.R = 1,46a
.
.r = 1,37a
.
.A = 4.25a² |
...
Für den 9/4-Stern, also für p=9 und q=4 gilt:
| Winkel an der Spitze alpha = [(p-2q)/p]*180° = (1/9)*180°
= 20°
Seitenlänge s = a*sin(180°q/p)/sin(180°/p)
= a*(sin 80°/sin 20°)
Grundseite einer Zacke c = a*{sin[(p-2q)/2p]*180°}/{cos[(q-1)/p]*180°}
= a*(sin 10°/cos 60°)
Schenkel einer Zacke b = (a/2)/{cos[(q-1)/p]*180°}
= (a/2)/cos 60° = a
Radius des Umkreises R = (a/2)/sin(180°/p)
= (a/2)/sin 20°
Radius des Inkreises r = r = (a/2)/tan(180°/p)
= (a/2)/tan 20°
Flächeninhalt A = (1/4) {1/tan(180°/p)-tan[(q-1)/p*180°]}pa²
= (9/4)/(1/tan 20°-tan 60°)a² |
.Gerundete Werte.
.
.s = 2,88a ...........
.
.c = 0,35a
.
.b = a
.
.R = 1,46a
.
.r = 1,37a
.
.A = 2,28a² |
Verschiedenes top
Alle Diagonalen
... |
... ... |
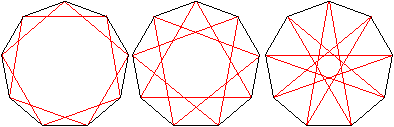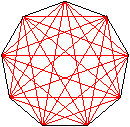Das sind noch einmal die drei Sterne im regelmäßigen
Neueneck.
Mehr auf meiner Webseite Regelmäßiges
Neuneck |
Drachenvierecke
... .... |
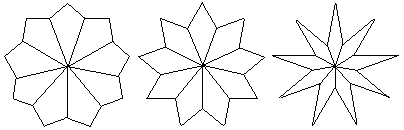Gibt man neun bestimmte Drachenvierecke vor, so kann
man aus ihnen ein Nonagramm legen. |
Räumlich
... ... |
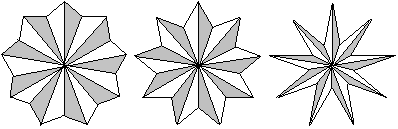Fügt man noch die langen Diagonalen hinzu und färbt
Dreiecke, so erscheinen die Sterne räumlich. |
Kombination
der Sterne
...
...
Keltischer
Knoten
... ... |
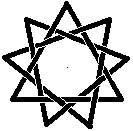Zeichnet man die Linien des zusammengesetzten Nonagramms
dicker und dann abwechselnd Brücken und Unterführungen, so entsteht
ein geflochtener Stern. |
Noch
zwei bunte Figuren
Überschagene
regelmäßige Neunecke top
... ... |
 ... |
. |
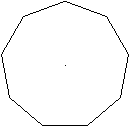
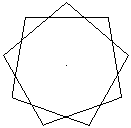
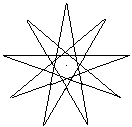
Die Nonagramme kann man auch als überschlagene Neunecke
ansehen, bei denen die neun Eckpunkte durch Linien verbunden werden, die
sich überschneiden. |
Es gibt noch weitere überschlagene Achtecke, darunter
sind bizarre Figuren.
...
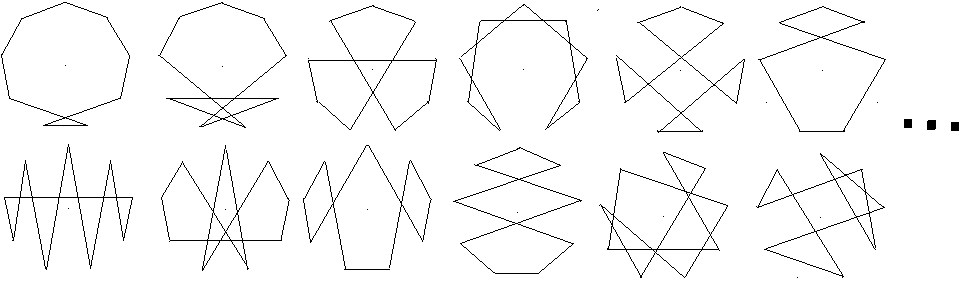
Sie sind Hamiltonkreise,
da Punkte durch eine geschlossene Linie verbunden werden.
Enneagramm
top
... ... |
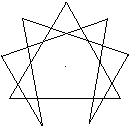Es sieht so aus, als sei die nebenstehende Figur eine
weitere Figur, die aus einer geschlossenen Linie entsteht. |
... |
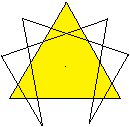Die Figur ist aber ein zusammengesetztes Nonagramm.
Sie besteht aus einer Figur mit sechs Ecken und einem
gleichseitigen Dreieck. |
Der
Name Enneagramm leitet sich aus dem Griechischem her und bedeutet nach
de.wikipedia Neun-Schrift.
Die Figur ist im Internet häufig
zu finden. Esoteriker benutzten sie, um die Zahl Neun in ihren Theorien
zu veranschaulichen.
Mehr kann man auf der deutschen
Wikipedia-Seite Enneagramm nachlesen.
Zum
Begriff
Folgt man den Wikipedia-Seiten
Enneagram_(geometry)
und Stern (Geometrie), so sollte diese Webseite nicht Nonagramm heißen,
sondern Enneagramm. Das ist wegen der Wortherkunft auch berechtigt, da
das Wort Nonagramm eine unschöne lateinisch/griechische Herkunft hat.
Doch ich folge Mathworld (URL unten).
Gefalteter Stern
top
... ... |
... ... |
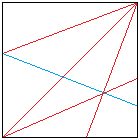Die Anleitung zu diesem einfachen und schönen Origami-Stern
ist im Internet z.B. mit "Gefalteter Stern mit neun Zacken" zu finden.
Er ist einfach zu falten, aber leider nicht sehr stabil. |
 |
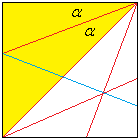Der Stern ist kein Nonagramm. Für diesen Stern ist
der Winkel an der Spitze 2*alpha = 45°. |
Nonagramm im Internet
top
Deutsch
Online-Rechner
Doppelter
Stern
Wikipedia
Stern
(Geometrie), Enneagramm
Englisch
Eric W. Weisstein (World of Mathematics)
Nonagram,
Nonagon,
Star
Polygon
Wikipedia
Enneagram
(geometry),
Star
polygon
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
01/2024 Jürgen Köller
top |
