|
Was ist ein regelmäßiges
Fünfeck?
|
Ein regelmäßiges Fünfeck oder regelmäßiges
Pentagon ist ein Vieleck mit
fünf gleich langen Seiten und
fünf gleich großen Innenwinkeln. |
Auf dieser Seite heißt das regelmäßige Fünfeck
meist einfach Fünfeck.
Größen
des Fünfecks
top
Winkel im Fünfeck
...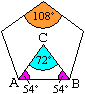 ... ... |
Der Winkel an der Spitze des Bestimmungsdreiecks bzw.
der Mittelpunktwinkel ist 360°/5=72°.
Dann sind die Winkel an der Basis 54°.
Der Innenwinkel eines Fünfecks hat folglich die
Größe 108°. |
Formeln
Ein regelmäßiges Fünfeck ist im Allgemeinen
durch die Seitenlänge
a gegeben.
Daraus lassen sich der Flächeninhalt A, der
Umfang
U, die Radien R und r von Um- und Inkreis,
die Länge
d der Diagonalen und die Höhe h berechnen.
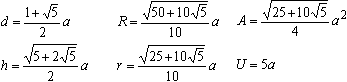
|
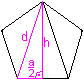
Diagonale und Höhe:
|
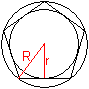
Umkreis und Inkreis:
|
Herleitung
der Formeln
Diagonale d
...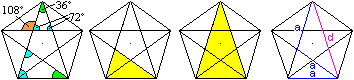 ... ... |
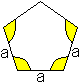
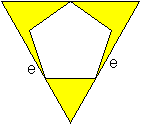
Mit Hilfe der Winkel erkennt man, dass die beiden gelben
Dreiecke gleichschenklig und ähnlich sind. Dann gilt (d-a):a=a:d oder
d(d-a)=a². Diese quadratische Gleichung in d hat die (positive) Lösung
d=[1+sqrt(5)]/2*a. |
Man kann aus der Rechnung ablesen, dass die Diagonalen sich
im Verhältnis des Goldenen Schnittes teilen. Mehr darüber findet
man auf meiner Seite
Sterne. Da wird auch das Pentagramm
besprochen, das von den Diagonalen gebildet wird.
Höhe h
.. .... ....
|
Es gilt d²=(1/4)[(1+sqrt(5)]²=[(1/4)[6+2sqrt(5)]a².
Nach dem Satz des Pythagoras gilt weiter h²+(a/2)²=d². |
Daraus folgt h²=d²-(a/2)²=(1/4)(4d²-a²)=(1/4)[5+2sqrt(5)]a².
Dann ist h=[sqrt(5+2*sqrt(5))]/2*a, wzbw.
Radius R des Umkreises, Radius r
des Inkreises, Flächeninhalt A
..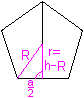 .... .... |
Nach dem Satz des Pythagoras gilt R²=(a/2)²+(h-R)².
Daraus folgt nach längerer Rechnung R=[sqrt(50+10*sqrt(5))]/10*a. |
Weiter gilt r=[sqrt(25+10*sqrt(5))]/10*a,
hergeleitet aus r²=R²-(a/2)².
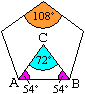 |
A=5*DreieckABC=5*ar/2=[sqrt(25+10*sqrt(5))]/4*a² |
Vom Vieleck zum
Fünfeck top
Das Fünfeck ist der Spezialfall n=5 des Vielecks.
Kennt man also Formeln des Vielecks, so kann man die
des Fünfecks berechnen.
Ist
für ein Vieleck die Seite a gegeben, so gilt
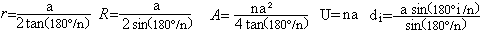
i=1,2,...n-1.
In der Rechnung treten für
n=5 drei Werte trigonometrischer Funktionen auf, nämlich tan(36°),
sin(36°) und sin(72°).
Es gilt tan(36°)=sqrt[5-2sqrt(5)], sin(36°)=(1/4)sqrt[10-2sqrt(5)]
und sin(72°)=(1/4)sqrt[10+2sqrt(5)].
Damit ergibt sich
r = a/[2tan(36°)] = (1/2)a/sqrt[5-2sqrt(5)]
R = a/[2sin(36°)] = (1/2)a/sqrt[10-2sqrt(5)]
A = 5a²/[4tan(36°)] =(5/4)a²/sqrt/[5-2sqrt(5)]
d2 = d = a sin(72°)/[sin((36°)] =(1/4)a
sqrt[10+2sqrt(5)]/sqrt[10-2sqrt(5)]
Formt man die Terme um, so ergeben sich die Werte oben.
Exemplarisch wird der Radius des Inkreises noch einmal
auf diesem Wege berechnet.
r= (1/2)a/sqrt[5-2sqrt(5)] = (1/2)a sqrt[5-2sqrt(5)]/[5-2sqrt(5)]
= (1/2)a sqrt[5-2sqrt(5)][5+2sqrt(5)]/5
=(1/10)a sqrt[5-2sqrt(5)]sqrt[45+20sqrt(5)] = (1/10)a
sqrt{[5-2sqrt(5)][45+20sqrt(5)]} =(1/10)a sqrt[25+10sqrt(5)]
Erzeugen eines
Fünfecks
top
Zeichnen mit Zirkel und Geodreieck
Das ist die einfachste Methode.
...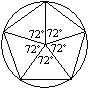 ... ... |
Zeichne 4 (besser zur Kontrolle 5) Winkel von 72°
nebeneinander mit einem gemeinsamen Scheitelpunkt. Beginne mit einem vertikalen
Schenkel.
Zeichne einen Kreis um den Scheitelpunkt. Die Schnittpunkte
des Kreises mit den Schenkeln sind die Eckpunkte eines Fünfecks. |
Konstruktion
Gegeben sei die Strecke a. Das
Fünfeck soll nur mit Zirkel und Lineal gezeichnet werden.
Man
nutzt in der folgenden Konstruktion aus, dass die Diagonalen im Fünfeck
gleich lang sind und sich im Verhältnis des Goldenen Schnittes teilen.
...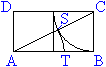 ... ... |
Gegeben sei die Strecke d=AB. Der
Punkt T teilt sie im Verhältnis des Goldenen Schnittes. Die Beschreibung
der Konstruktion findet man auf meiner Seite
Doppelquadrat.
Die Strecke AB wird die Diagonale eines Fünfecks. |
Die weitere Konstruktion:
...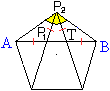 ... ... |
Die Punkte A, B und T sind also
gefunden.
Trage die Strecke TB von A aus
auf AB ab. Der Punkt P1 entsteht.
Zeichne um T und P1
Kreise mit dem Radius TB. Der Punkt P2
entsteht.
Verbinde den Punkt P2
mit A und B. Der Winkel AP2B ist
der Innenwinkel von 108° des Fünfecks. |
... ... ...
|
Trage an die gegebene Strecke a den Winkel von 108°
beidseitig an.
Trage die Strecke a auf den freien Schenkeln ab.
Trage wiederum an den neuen Strecken a den Winkel von
108° an.
Die freien Schenkel schneiden sich im fünften Eckpunkt
des Fünfecks. |
Basteln
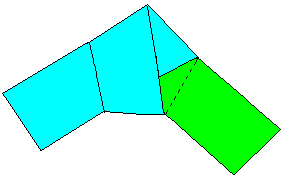
Bindet man mit einem Papierstreifen einen Knoten ("Überhandknoten")
und zieht vorsichtig an den Papierenden, so entsteht erstaunlicherweise
ein Fünfeck.
Zwei Quadrate
im Fünfeck
top
... ... ...
|
 ... ...
|
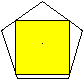
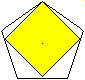
Es gibt zwei Möglichkeiten, ein möglichst großes
Quadrat in das Fünfeck einzupassen. |
...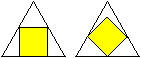 ... ... |
Wie beim gleichseitigen Dreieck
sind die Flächeninhalte nach der Zeichnung in etwa gleich, so dass
eine Rechnung klären muss, welche Größenbeziehung besteht. |
1) Eine Quadratseite liegt
parallel zur Grundseite des Fünfecks.
...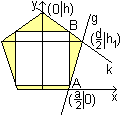 ... ... |
Man legt die Figuren in ein kartesisches Koordinatensystem.
Die Eckpunkte A und B des Quadrats liegen auf den Geraden
g und k.
Ihre Gleichungen werden bestimmt. |
g:
Es wird die Zwei-Punkte-Darstellung gewählt.
(y-0)/(x-a/2) = (h1-0)/(d/2-a/2) oder y =
2h1/(d-a)(x-a/2) oder y=2h1/(d-a)x-h1a/(d-a).
h:
Die Gleichung kann man direkt ablesen. y = -2(h-h1)/dx+h
Die Figur im Fünfeck ist ein Quadrat,
wenn die Differenz der y-Werte von A und B gleich dem doppelten x-Wert
ist.
Die Seitenlänge des Quadrates ist dann e=2x.
Das führt zum Ansatz
[-2(h-h1)/dx+h] - [2h1/(d-a)x+ah1/(d-a)]=
2x
<=> [-2(h-h1)/d-2h1/(d-a)-2]x
=-h-ah1/(d-a)
<=> [2(h-h1)/d+2h1/(d-a)+2]x
=h+ah1/(d-a)
<=> x=[h+ah1/(d-a)]/[2(h-h1)/d+2h1/(d-a)+2)]
Es ist wohl nicht möglich, den Term wesentlich zu vereinfachen.
Deshalb übernimmt ein Computer eine Zahlenrechnung.
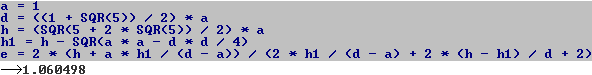
|
Die Quadratseite ist AB=1,0605a. |
2) Das Quadrat steht auf
der Spitze.
...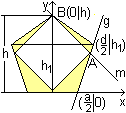 ... ...
|
Man legt die Figuren in ein kartesisches Koordinatensystem.
Der Eckpunkt A und B des Quadrats liegt auf den Geraden
g und k. Deshalb werden ihre Gleichungen bestimmt. |
g:
Wie oben gezeigt ist die Gleichung y=2h1/(d-a)x-h1a/(d-a)
m:
Die Gleichung kann man direkt ablesen. y = -x+h.
Punkt A ist der Schnittpunkt beider Geraden.
Dann ist 2h1/(d-a)x-h1a/(d-a)
= x+h oder 2h1/(d-a)x+x = h+h1a/(d-a) oder
x = [(h+h1a/(d-a)]/[2h1/(d-a)+1]
Die Seite des Quadrats ist dann e=sqrt(2)x.
Es ist wohl nicht möglich, den Term wesentlich zu
vereinfachen.
Deshalb übernimmt ein Computer eine Zahlenrechnung.
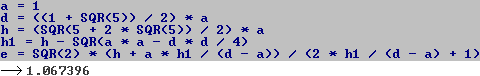
|
Die Quadratseite ist AB=1,0674a. |
Ergebnis: Das zweite Quadrat ist größer als das
erste, und zwar nur um 0,65%.
Dreieck
und Fünfeck
An Stelle des Quadrates können gleichseitige Dreiecke
im Fünfeck liegen.
Dreiecke um das Fünfeck zu legen ist vielleicht
auch interessant.
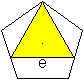
e=2 [(h+ah1/(d-a)]/([2h1/(d-a)+sqr(3)],
gerundet 1,280a
|
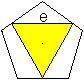
e=2h/[2(h-h1)/d+sqrt(3)]
gerundet 1,252a
|
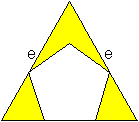
e=d+(2/3)sqrt(3)h1, gerundet 2,716a
|
e=d+(2/3)sqrt(3)(h-h1), gerundet 2,297a
|
Die Formeln für die Seitenlängen
der inneren Dreiecke leitet man wie bei den Quadraten im Fünfeck her.
Die Formeln der Umdreiecke ergeben sich aus dem zweiten Strahlensatz.
Figuren im Fünfeck
top

Folgen aus Fünfecken
top
Fünfeckszahlen top
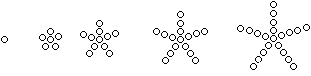
Die Folge ist
1, 6, 11, 16, 21, ... allgemein 5n-4 (n=1,2,3,...)
|
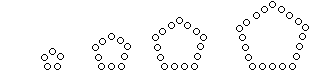
Die Folge ist
5, 10, 15, 20, ..., allgemein 5n
|
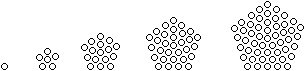
Die Folge ist
1, 6, 16,31, 51..., allgemein (5n²-5n)/2+1
|
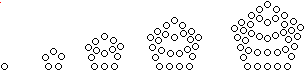
Die Folge ist
1, 5, 12, 22, 35,... allgemein (3n-1)n/2
|
Körper und Fünfecke
top
Deltaeder sind Körper, die nur von gleichseitigen
Dreiecken begrenzt werden. Unter ihnen gibt es zwei konvexe Körper,
bei denen das regelmäßige Fünfeck eine "tragende" Rolle
spielt.
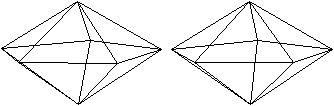
Der erste Körper ist die pentagonale
Doppelpyramide.
... ... ...
|
Auf ein Fünfeck werden zu
beiden Seiten hin gerade Pyramiden mit gleichseitigen Dreiecken als Seitenflächen
gesetzt. |
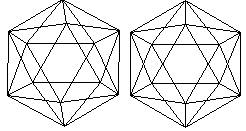
Der zweite Körper ist das Ikosaeder.
... ... ...
|
Ein Ikosaeder entsteht, wenn man zwei parallel liegende
Fünfecke um einen Winkel von 36° gegeneinander verdreht und mit
einem Netz aus zehn gleichseitigen Dreiecken verbindet. |
Es entsteht ein Antiprisma. Schließlich setzt man auf
die Fünfecke Pyramiden mit gleichseitigen Dreiecken als Seitenflächen.
Mehr über Deltaeder findet man an anderer Stelle.
Zwölf Fünfecke
bilden den platonischen Körper
Pentagondodekaeder.
Die archimedische Körper
Ikosidodekaeder,
kleines
Rhombenikosidodekaeder und abgeschrägtes
Dodekaeder enthalten Fünfecke.
Fünfeck
falten top
Exaktes Fünfeck
...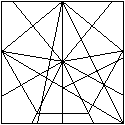 ... ... |
Es gibt auch die Möglichkeit, ein regelmäßiges
Fünfeck im Quadrat exakt zu falten.
Das Fünfeck entsteht nach 13 Faltungen.
Auf der folgenden Webseite findet man ein Anleitung und
etwas Mathematik dazu.
Link: Laszlo C Bardos Fold
a Regular Pentagon
Weiteter Link: Mathematikus Falten
eines Fünfecks |
Beinahe ein Fünfeck
Zum populären gefaltenen Fünfeckstern benötigt
man ein regelmäßiges Fünfeck. Es gibt eine Möglichkeit.
es schon mit fünf Faltungen herzustellen. Es ist kein exaktes regelmäßiges
Fünfeck, aber ein kennzeichnender Winkel von 36° ist 36,87°.
Das ist nur 2% zu groß. Das spielt beim Falten keine Rolle.
...... |
 |
Mehr auf meiner Webseite
Gefalteter
Fünfeckstern
Es folgt noch ein Hinweis auf meine neue Seite von 2023
Pentagramm.
Ungefähr ein
Fünfeck
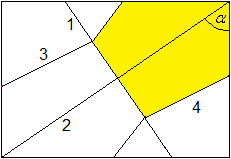 |
Bei einem A4-Blatt beträgt der Winkel alpha zwischen
der Diagonale und der kleineren Seite gerundet 54,7°.
Durch vier Tal-Faltungen in der Reihenfolge 1, 2, 3,
4 erzeugt man ein Fünfeck.
Bei einem regelmäßige Fünfeck beträgt
der Winkel an der Spitze 104° und alpha wäre 52°.
Ergebnis: Das gefaltete Fünfeck ist fast regelmäßig.
Die Abweichung beträgt 2,7°. |

Quelle: How
to fold PENTAGON from A4 (Video)
Weiterer Link: Folded
Pentagon
Fünfecke im
Internet top
Deutsch
Claus Schönleber / Frank Klinkenberg-Haaß
Goldene
Schnittmuster
Diana Todt
Falten
eines regelmäßigen Fünfecks (pdf-Datei)
Rainer Kaske
Konstruktion
eines Fünfecks
Wikipedia
Fünfeck,
Pentagramm,
Drudenfuß
(Symbol), Formelsammlung
Trigonometrie
Englisch
Alexander Bogomolny (Cut-the Knot)
Inscribing
a regular pentagon in a circle - and proving it (Scott E. Brodie)
cut-the-knot.org
Regular
Pentagon Inscribed in Circle by Paper Folding
David Dureisseix (Institut National des Sciences Appliquées
de Lyon)
Folding
optimal polygons from squares
Eric W. Weisstein (MathWorld)
Pentagon,
Pentagram,
Pentaflake,
Five
Disks Problem, Hoehns
Theorem
Wikipedia
Pentagon,
Pentagram,
Pentagrammic
prism
Referenzen top
Jan Gullberg: Mathematics- From the Birth of Numbers,
New York, London 1997 (ISBN0-393-04002-X)
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage
https://www.mathematische-basteleien.de/
©
2004 (ergänzt 2010) Jürgen Köller
top |




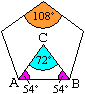 ...
...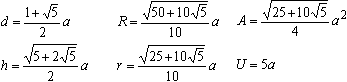


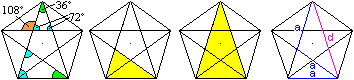 ...
... ....
.... ...
... ...
... ...
... ...
... ...
... ...
... ...
...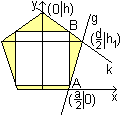 ...
...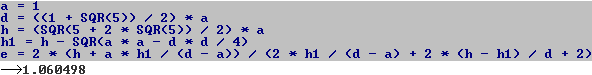
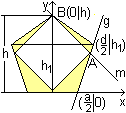 ...
...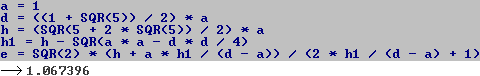





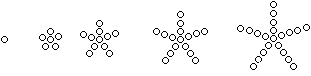
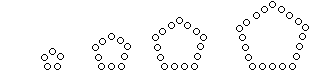
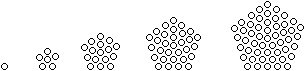
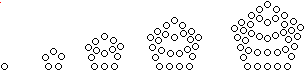
 ...
... ...
... ...
...

