|
Was ist eine figurierte Zahl?
... ... |
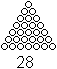Eine figurierte Zahl (oder Figurenzahl) ist eine natürliche
Zahl, die man durch eine Figur - zum Beispiel gelegt aus Kugeln - darstellen
kann.
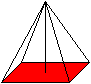
Das gleichseitige Dreieck stellt die Dreieckszahl 1+2+3+4+5+6+7=28
dar. |
Eine figurierte Zahl steht nicht
für sich allein, sie ist das Glied in einer Folge von Zahlen.
 ...
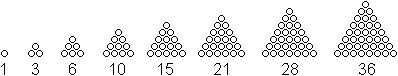So sind zum Beispiel die Vielfachen einer Zahl wie 6 und
sogar die natürlichen Zahlen figurierte Zahlen.
... ...
|
|
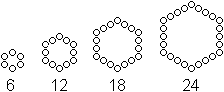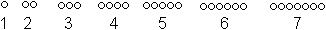
Doch man erwartet schon,
dass die Figuren komplexer sind. Figurierte Zahlen beziehen sich meist
- ausgehend von den Dreiecken oben - auf ausgefüllte regelmäßige
Vielecke und auf platonische Körper.
Sie heißen dann Polygonzahlen bzw. Polyederzahlen.
Figurierte Zahlen sind ein
beliebter Gegenstand der Unterhaltungsmathematik.
Ich begegnete ihnen immer wieder bei den Recherchen für
meine Seiten.
Hier sollen sie einmal im Zusammenhang vorgestellt werden.
Fast alle figurierten Zahlen
auf dieser Seite findet man auch in der Sammlung OEIS (The On-Line Encyclopedia
of Integer Sequences). Ich gebe hier die Verlagerung der externen Links
ans Ende auf und weise bei jeder Folge auf den Fundort bei OEIS hin. Es
ergeben sich leichte Abweichungen, da auf dieser Seite die Zahl 0 nicht
als erstes Glied der Folgen zugelassen wird, bei OEIS oft schon.
Polygonzahlen top
Wie man Polygonzahlen mit Hilfe regelmäßiger
Vielecke erzeugt, wird anhand der Sechseckzahl 45 erklärt.
... ... |
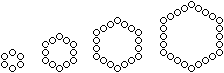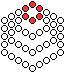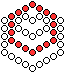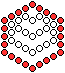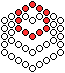
Man gibt vier sechseckige Rahmen aus Kugeln vor mit den
Seitenlängen 2, 3, 4 und 5. |
... ... |
... ... |
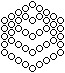Dann setzt man die drei kleineren Sechsecke nacheinander
in das große Sechseck der Seitenlänge 5 und schiebt sie in die
obere Ecke. Die endgültige Figur enthält dann 45 Kugeln. |
Mit dieser Methode ermittelt
man die Polygonzahlen, hier aufgeführt der Reihe nach.
Folge der Dreieckszahlen
 ...
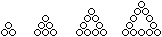bereitgestellt.
|
 ......
|
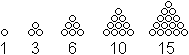Die Folge der Dreieckszahlen wird durch die Gleichung
D(n)=(1/2)n(n+1) beschrieben.
OEIS: A000217
Triangular numbers: a(n) = C(n+1,2) = n(n+1)/2 = 0+1+2+...+n.
Mehr findet man auf meiner
Seite
Dreieckszahlen.
Folge
der Quadratzahlen
 ...
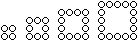bereitgestellt
|
 .....
|
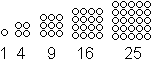Die Folge der Quadratzahlen
wird durch die Gleichung Q(n)=n² beschrieben.
OEIS: A000290
The squares: a(n) = n^2.
Mehr findet man auf meiner
Seite Quadratzahlen.
Folge
der Fünfeckzahlen
 ...
bereitgestellt.
|
 ...
|
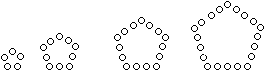
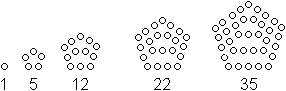
Die Folge der Fünfeckzahlen
wird durch die Gleichung F(n)=(1/2)n(3n-1) beschrieben.
OEIS: A000326
Pentagonal numbers: n*(3*n-1)/2.
Folge
der Sechseckzahlen
...
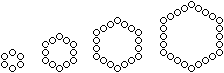bereitgestellt.
|
 ....
|
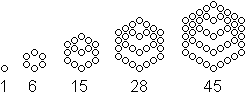Die Folge der Sechseckzahlen
wird durch die Gleichung S(n)=n(2n-1) beschrieben.
OEIS: A000384
Hexagonal numbers: n*(2*n-1).
Folge
der Achteckzahlen
Es folgen noch die Achteckzahlen. Sie tauchen weiter
unten als Sternzahlen wieder auf.
... ... |
Die Gleichung ist A(n)=n(3n-2). |
OEIS: A000567
Octagonal numbers: n*(3*n-2). Also called star numbers.
Weitere Folgen von Zahlen
mit ihren Figuren können so konstruiert werden.
Beweise top
Es stellt sich die Frage, wie man eine Formel für
das n-te Glied der Folge der Polygonzahlen herleitet und beweist. Das soll
zunächst an Hand der Sechseckzahlen dargestellt werden, und zwar auf
zwei Wegen.
Erster Beweis
der Formel S(n)=n(2n-1)
Die Sechseckzahlen bilden eine arithmetische Folge zweiter
Ordnung. Bildet man nämlich die Differenzen nebeneinander liegender
Glieder und dann von dieser Differenzenfolge wiederum die Differenzen,
so erhält man die konstante Folge mit der Konstanten 4.
01 06 15
28 45 66
91 120 ...
05 09
13 17 21 25
29 ...
04 04 04
04 04 04 ...
Folgen dieser Art haben die Darstellung S(n)=an²+bn+c.
Die Variablen a, b und c bestimmt man mit Hilfe der ersten
drei Glieder.
Es gilt S(1)=1,
S(2)=6
und S(3)=15. |
oder (I) a+b+c=1,
(II) 4a+2b+c=6
und (III) 9a+3b+c=15. |
(II)-(I) ergibt 3a +b=5 (IV).
(III)-(II) ergibt 5a+b=9 (V).
(V)-(IV) ergibt 2a=4 oder a=2. |
(IV) ergibt 6+b=5 oder b=-1.
(I) ergibt 2-1+c=1 oder c=0.
Ergebnis: S(n)=2n²-n=n(2n-1) |
Zweiter
Beweis der Formel S(n)=n(2n-1)
... ... |
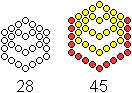Man macht sich zunutze, dass jedes Glied der Folge aus
dem vorhergehenden entsteht.
Die 5. Figur entsteht z.B., indem man zur 4. Figur 4*4+1
Kugeln hinzufügt. |
Die (n+1)-te Figur entsteht, indem man zur n-ten Figur 4*n+1
Kugeln hinzufügt.
Nach dieser Vorbereitung
wird die Methode der vollständigen Induktion angewandt.
Die Formel S(n)=n(2n-1) gilt
für n=1 und n=2:
S(1)=1*(2-1)=1 und S(2)=2*(2*2-1)=6.
Es muss gezeigt werden, dass
die Formel auch gilt, wenn man in der Formel n durch n+1 ersetzt unter
der Voraussetzung, dass sie für n gilt.
Zu zeigen ist also: S(n+1)=(n+1)[2(n+1)-1] oder S(n+1)=(n+1)(2n+1)
oder S(n)=2n²+3n+1.
Es gilt tatsächlich
S(n+1)=S(n)+4n+1=n(2n-1)+4n+1=2n²-n+4n+1=2n²+3n+1,
wzbw.
Verallgemeinerung
Es gibt eine Formel, nach der das n-te Glied der r-ten
Polyederzahl Fr(n) mit einem Term angegeben werden kann.
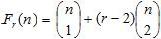(1), Seite 52
Überprüfung für
r=6
F6(n)=n!/(n-1)!+(6-2){n!/[(n-2)!2!]}=n+4*[n(n-1)/2]=n+2n(n-1)=2n²-n=n(2n-1)=S(n)
Der Beweis der Formel gelingt wieder
mit der Methode der vollständigen Induktion. Man muss sich dazu klar
machen, dass die (n+1)-te Figur entsteht, indem man zur n-ten Figur (r-2)*n+1
Kugeln hinzufügt.
Zentrierte
Polygonzahlen top
|
......
|
... ... |
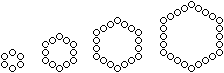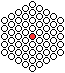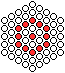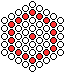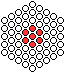Zentrierte Polygonzahlen entstehen, indem man eine Kugel
vorgibt und um sie herum größer werdende Vielecke legt, immer
mit einer um 1 größeren Seitenlänge. |
Das sind die ersten zentrierten
Polygonzahlen.
Folge der zentrierten Dreieckszahlen
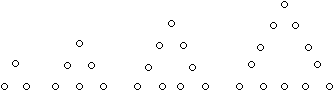
bereitgestellt
|
|
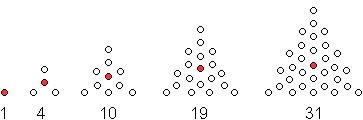
Die Gleichung ist
ZD(n)=(1/2)(3n²-3n+2). |
OEIS: A005448
Centered triangular numbers: 3n(n-1)/2 + 1.
Folge
der zentrierten Quadratzahlen
 ...
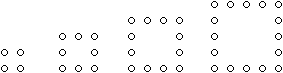bereitgestellt
|
 ...
|
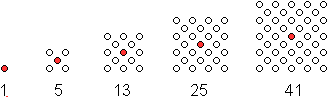
Die Gleichung ist
ZQ(n)=2n²-2n+1. |
OEIS: A001844
Centered square numbers: 2n(n+1)+1
Folge
der zentrierten Fünfeckzahlen
...
bereitgestellt
|
 ...
|
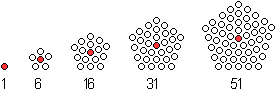
Die Gleichung ist
ZF(n)=(1/2)(5n²-5n+2). |
OEIS: A005891
Centered pentagonal numbers: (5n^2+5n+2)/2
Folge
der zentrierten Sechseckzahlen (auch Hexnumber bei Mathworld genannt)
...
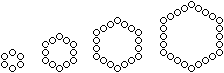bereitgestellt
|
 ...
|
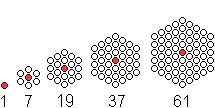
Die Gleichung ist
ZS(n)=3n²-3n+1
|
OEIS: A003215
Hex (or centered hexagonal) numbers: 3*n*(n+1)+1
Folge
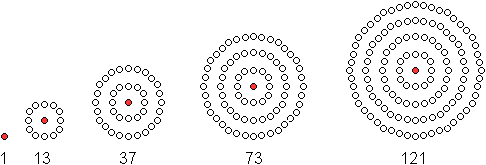
der zentrierten Zwölfeckzahlen
Es folgt noch die Folge der Zwölfeckzahlen.
Sie
tauchen weiter unten als Sternzahlen wieder auf.
... ...
|
Die Gleichung ist
ZZ(n)=6n(n-1)+1. |
OEIS: A003154
Centered 12-gonal numbers. Also star numbers: 6*n*(n-1) + 1.
Weitere Folgen von Zahlen
mit ihren Figuren können so konstruiert werden.
Verallgemeinerung
Will man eine Formel für das n-te Glied der Folge
der zentrierten Zahlen herleiten, geht man am besten auf die Dreieckszahlen
zurück.
... ... |
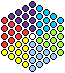Für der Zeichnung gilt ZS(5)=6*D(4)+1. Die Verallgemeinerung
ist ZS(n)=6*D(n-1)+1. |
So wie das Sechseck kann man jede Figur der zentrierten Zahlen
in Dreiecke aufteilen.
Es gilt allgemein für die k-te zentrierte Zahl ZFk(n)=k*D(n-1)+1
mit D(n-1)=(1/2)n(n-1).
Das führt zu ZFk(n)=(1/2)[kn(n-1)+2].
Pyramidenzahlen top
Die Pyramidenzahlen entstehen, wie der Name sagt, mit
Hilfe von Pyramiden.
Es hat sich so ergeben, dass
in den folgenden Zeichnungen die Kreise durch Rechtecke ersetzt werden.
Folge
der Tetraederzahlen
... ...... |
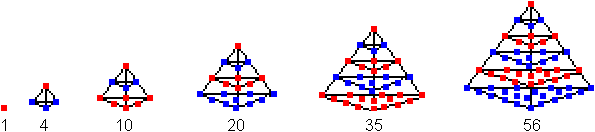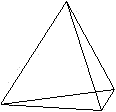
Die Folge der Tetraederzahlen
ist die Reihe zur Folge der Dreieckszahlen. |
Aus 1, 3, 6, 10, 15, 21 wird 1, 1+3, 1+3+6, 1+3+6+10, 1+3+6+10+15,
1+3+6+10+15+21, ....
Die ersten Tetraederzahlen sind also 1, 4, 10, 20, 35,
56, 84, 120, 165, 220, ...
Die allgemeine Formel ist
T(n)=(1/6)n(n+1)(n+2).
OEIS: A000292
Tetrahedral (or triangular pyramidal) numbers: a(n) = C(n+2,3) = n*(n+1)*(n+2)/6.
Folge
der quadratischen Pyramidenzahlen
... ...... |
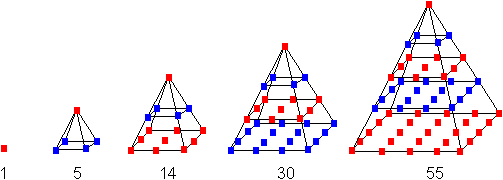Die Folge der quadratischen Pyramidenzahlen
ist die Reihe zur Folge der Quadratzahlen.
Aus 1, 4, 9, 16, 25 wird
1, 1+4, 1+4+9, 1+4+9+16, 1+4+9+16+25,
... |
Die quadratischen Pyramidenzahlen sind
also
1, 5, 14, 30, 55, 91, 140, 204, 285, 385, ...
Die allgemeine Formel ist
QP(n)=(1/6)n(n+1)(2n+1).
OEIS: A000330
Square pyramidal numbers: 0^2 + 1^2 + 2^2 +...+ n^2 = n*(n+1)*(2*n+1)/6.
Folge
der fünfseitigen Pyramidenzahlen
... ... |
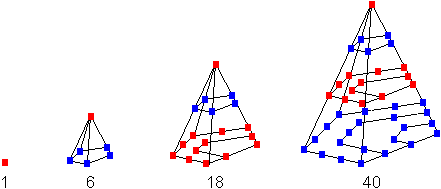Die Folge der fünfeckigen
Pyramidenzahlen
ist die Reihe zur Folge der Fünfeckzahlen.
Aus 1, 5, 12, 22, ... wird
1, 1+5, 1+5+12, 1+5+12+22, .... |
Das n-te Glied der Folge
der fünfseitigen Pyramidenzahlen ist FP(n)=(1/2)n²(n+1).
Die ersten
fünfseitigen Pyramidenzahlen sind also 1, 6, 18, 40, 75, 126, 196,
288, 405, 550, ...
OEIS: A002411
Pentagonal pyramidal numbers: n^2*(n+1)/2.
Verallgemeinerung
| Das n-te Glied der r-seitigen Pyramidenzahl ist |
 |
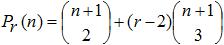(1), Seite 52
Überprüfung für
r=5
P5(n)=(n+1)!/[(n-1)!2!]+3*{(n+1)!/[(n-2)!3!]}=(1/2)[n(n+1)+(n+1)n(n-1)]=(1/2)(n³+n²)=(1/2)[n²(n+1)]
Herleitung der Formel für
r=5, also FP(n)=(1/2)n²(n+1)=(1/2)n³+(1/2)n²
Das k-te Glied der Fünfeckzahlen ist (1/2)k(3k-1).
| Die Reihe dazu ist |
 |
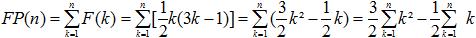Dann ist weiter FP(n) = (3/2)[(1/6)n(n+1)(2n+1)]-(1/2)[(1/2)n(n+1)]
= ... = (1/2)n³+(1/2)n², wzbw.
Auf dem gleichen Wege kann
man die allgemeine Formel für die r-seitige Pyramidenzahl herleiten,
doch mit viel mehr Aufwand.
Polyederzahlen top
Die Polyederzahlen entstehen mit Hilfe platonischer Körper.
Folge der Tetraederzahlen
| ...... |
Die Tetraederzahlen werden im Kapitel Pyramidenzahlen
vorgestellt |
Folge
der Oktaederzahlen
Das Oktaeder entsteht, indem man
die quadratische Pyramide an der Grundfläche spiegelt.
... ...... |
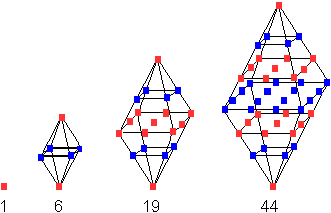Die quadratischen Pyramidenzahlen sind
1, 5, 14, 30, 55, ...
Durch das Spiegeln an der Grundfläche der quadratischen
Pyramide erhält man die Oktaederzahlen. Man addiert dazu zu jeder
quadratischen Pyramidenzahl die vorhergehende.
Das führt zu 1, 5+1, 14+5, 30+14, 44+19, ...
Die allgemeine Formel ist O(n)=(1/3)(2n³+n). |
Die ersten Oktaederzahlen
sind also 1, 6, 19, 44, 85, 146, 231, 344, 489, 670, ...
OEIS: A005900
Octahedral numbers: (2n^3 + n)/3.
Folge
der zentrierten Oktaederzahlen
... ...... |
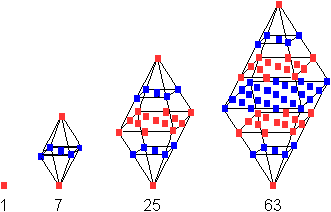Die Figur zu den zentrierten Oktaederzahlen entsteht
aus den Oktaederzahlen, indem man in jedes elementare 2x2 Quadrat einer
Ebene in die Mitte einen weiteren Stein hinzufügt.
Die allgemeine Formel ist ZO(n)=(1/3)(2n-1)(2n²-2n+3). |
Die ersten zentrierten Oktaederzahlen
sind 1, 7, 25, 63, 129, 231, 377, 575, 833, 1159, ...
OEIS: A001845
Centered octahedral numbers
Die folgenden Darstellungen
der Oktaederzahlen als Kugel- und Würfelpackungen machen klar, warum
es neben den Polyederzahlen die zentrierten
Polyederzahlen gibt.
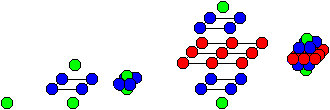
Oktaederzahlen 1, 6 und 19
|
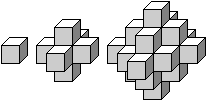
Zentrierte Oktaederzahlen 1, 7 und 25
|
Folge
der Kubikzahlen
Die Kubikzahlen werden
durch Würfel oder Kuben veranschaulicht.
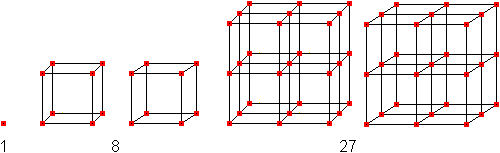
Die ersten Kubikzahlen sind
1, 8, 27, 64, 125, 216, 343, 512, 729, ...
OEIS: A000578
The cubes: a(n) = n^3.
Folge der zentrierten
Kubikzahlen
Addiert man zwei aufeinander folgende Kubikzahlen, so
entstehen die zentrierten Kubikzahlen.
|
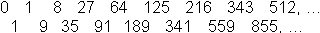
Das Bildungsgesetz ist ZK(n)=2n³-3n²+3n-1
=(2n-1)(n²-n+1)=n³+(n -1)³ |
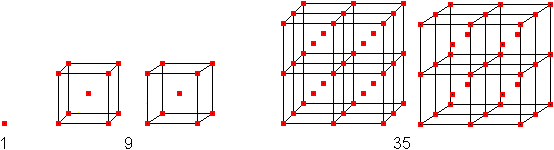
Die ersten zentrierten Kubikzahlen
sind 1, 9, 35, 91, 189, 341, 559, 855, ...
OEIS: A005898
Centered cube numbers: n^3 + (n+1)^3.
Sternzahlen top
... ... |
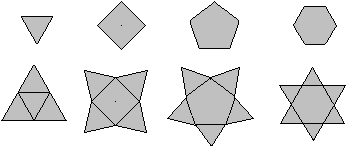Das ist eine Möglichkeit, Sterne
zu erzeugen:
Man gibt ein regelmäßiges Vieleck vor und setzt
auf die Seiten gleichseitige Dreiecke. |
Folge
der Zahlen des Dreieckssterns
... ...... |
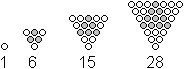Aus einem Dreieck und 3 weiteren Dreiecken entsteht ein
dreizackiger Stern.
Die sich daraus ergebende Folge wird mit dem Term
V(n) = D(n)+3*D(n-1) = (1/2)n(n+1)+3*(1/2)(n-1)n
= 2n²-n beschrieben. |
Es ergibt sich eine Teilfolge der Folge
der Dreieckszahlen, nämlich die mit ungeraden Nummern.
Folge der
Zahlen des Vierzacksterns
... ...... |
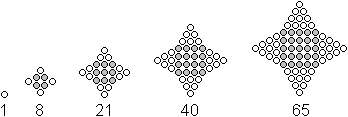Aus einem Quadrat und 4 Dreiecke entsteht ein vierzackiger
Stern.
Die sich daraus ergebende Folge wird mit der Formel
V(n) = Q(n)+4*D(n-1) = n²+4*(1/2)(n-1)n
= 3n²-2n
beschrieben. |
OEIS: A000567
Octagonal numbers: n*(3*n-2). Also called star numbers.
Folge
der Zahlen des Fünfzacksterns
... ...... |
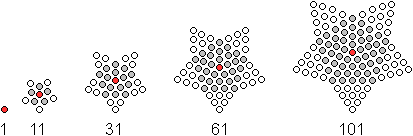Aus einem Fünfeck der zentrierten Fünfeckzahlen
und 5 Dreiecken entsteht ein fünfzackiger Stern. Die sich daraus ergebende
Folge wird durch die Formel
FS(n) = ZF(n)+5*D(n-1) = 5n²-5n+1
beschrieben. |
Bei OEIS steht nur: A062786
Centered 10-gonal numbers.
Sternzahlen
(Folge der Zahlen des Sechszacksterns)
... ...... |
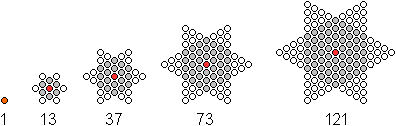Aus einem Sechseck der zentrierten Sechseckzahlen und
6 dreiecken entsteht ein sechszackiger Stern.
Die sich daraus ergebende Folge wird durch die Formel
SS(n) = ZS(n)+6*D(n-1) = 6n²-6n+1
beschrieben. |
OEIS: A003154
Centered 12-gonal numbers. Also star numbers: 6*n*(n-1) + 1.
Dreiecke und Quadrate
top
Folge zu einem Dreieck mit drei
Quadraten
... ...... |
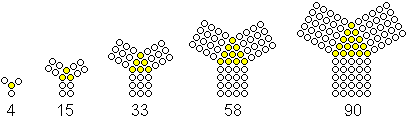Setzt man auf ein gleichseitiges Dreieck Quadrate, so
entsteht eine nebenstehende Figur. Sie erinnert an ein Bild zum Satz des
Pythagoras, bei dem aber in der Mitte ein rechtwinkliges Dreieck liegt. |
Die Zahlenfolge wird durch den Term D(n)+3*Q(n)=(1/2)n(7n+1)
beschrieben.
OEIS: A022265
n*(7n+1)/2.
Folge
zu einem Dreieck mit einem Quadrat
... ...... |
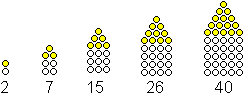Setzt man auf ein Quadrat nur ein Dreieck, so entsteht
ein unregelmäßiges Fünfeck.
Die Zahlen werden durch den Term
D(n)+Q(n)=n²+(1/2)n(n-1)=(1/2)(3n²+n) beschrieben. |
OEIS: A005449
Second pentagonal numbers: n * (3*n + 1) / 2.
Folge
der Schmetterlingszahlen
... ...... |
Setzt man auf ein Dreieck zwei Quadrate, so entsteht
ein konkaves Siebeneck. Die Folge wird durch den Term D(n)+2*Q(n)=(1/2)n(5n+1)
beschrieben. |
OEIS kennt diese Folge nicht: "Sorry, but the terms do not
match anything in the table."
Folge
zu einem Quadrat mit zwei Dreiecken
... ...... |
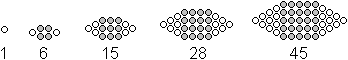Setzt man auf ein Quadrat zwei Dreiecke, so entsteht
ein konvexes Sechseck. Die Folge wird durch den Term Q(n)+2*D(n-1)=n²+2(1/2)(n-1)n=2n²-n
beschrieben. |
| ......... |
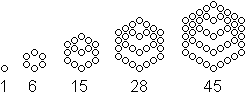Auch die Folge der Sechseckzahlen besteht aus diesen
Zahlen. |
OEIS: A000384
Hexagonal numbers: n*(2*n-1).
Folge
zu einem Quadrat mit drei Dreiecken
... ... |
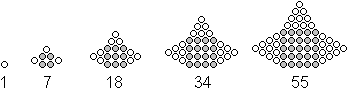Setzt man auf ein Quadrat drei Dreiecke, so entsteht
ein konkaves Siebeneck. Die Folge wird durch den Term Q(n)+3*D(n-1)=n²+3*(1/2)(n-1)n=(1/2)n(5n-3)
beschrieben. |
OEIS: A000566
Heptagonal numbers (or 7-gonal numbers): n(5n-3)/2.
Sonstige figurierte
Zahlen top
Folge der Rechteckzahlen
... ...... |
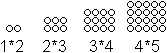Man kann sich beliebig viele Rechteckzahlen vorstellen.
Der Begriff wird eindeutig, wenn man fordert, dass die Seitenlängen
in der Folge der natürlichen Zahlen hintereinander stehen. |
Die Zahlen heißen 2, 6, 12, 20, 30, 42, 56, 72, 90,
110, ... mit der Beschreibung RE(n)=n(n+1).
Vielleicht tauchen sie nur
wegen ihrer Nähe zu den Dreieckszahlen in den Sammlungen figurierter
Zahlen auf.
... ... |
Es gilt RE(n)=2*D(n), wie in der Zeichnung illustriert. |
OEIS: A002378
Oblong (or promic, pronic, or heteromecic) numbers: n*(n+1).
Tannenbaum-Folge
... ... |
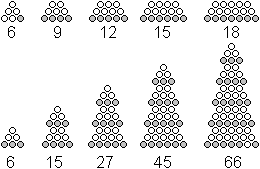Gibt man die arithmetische Folge mit 3n+3 von Trapezzahlen
vor, so bildet die zugehörige Reihe eine "Tannenbaum-Folge".
Das n-te Glied der Tannenbaum-Folge ist
(3*1+3)+(3*2+3)+(3*3+3)+...+(3*n+1)=3*(1+2+3...+n)+3n
=3*(1/2)n(n+1)+3n=(3/2)n(n+3) |
OEIS: Für die Zahlenfolge
wurde leider keine Übereinstimmung gefunden.
Folge
der dritten Fünfeckzahlen
... ...... |
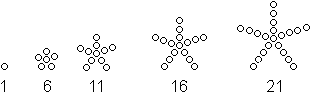Die Verbindungslinien zwischen dem Mittelpunkt eines
Fünfecks und den Eckpunkten bilden sternförmige Figuren.
Die zugehörige Folge ist arithmetisch und wird durch
den Term 5n-4 beschrieben. |
Folge
der Rhombendodekaeder-Zahlen
... ... |
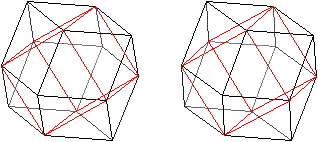Das Rhombendodekaeder
kann als ein Würfel aufgefasst werden, auf dessen Seitenflächen
quadratische Pyramiden aufgesetzt werden. |
Mit dieser Vorlage gelangt man zu den
Rhombendodekaeder-Zahlen.
... ... |
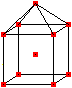Man gibt einen Würfel der zentrierten Kubikzahlen
vor, und setzt auf ein Quadrat eine Pyramide mit ihren quadratischen Pyramidenzahlen. |
... ... |
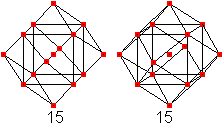Wiederholt man das für alle Würfelflächen,
so entsteht der nebenstehende Körper.
Das ist die Darstellung der zweiten Rhombendodekaeder-Zahl
15. |
Die n-te Rhombendodekaeder-Zahl erhält
man über die Formel RD(n)=ZK(n)+6*QP(n-1)
=(2n-1)(n²-n+1)+6*(1/6)(n-1)n(2n-1)=(2n-1)[(n²-n+1)+(n-1)n]=(2n-1)(2n²-2n+1).
Die
Anfangsglieder der Folge sind 1, 15, 65, 175, 369, 671, ...
OEIS: A005917
Rhombic dodecahedral numbers: n^4 - (n-1)^4.
Beziehungen
zwischen figurierten Zahlen top
Es ist ein beliebtes Thema, Beziehungen zwischen figurierten
Zahlen zu finden und zu veranschaulichen.
1
... ... |
In der Zeichnung gilt Q(5)=D(5)+D(4). Die Verallgemeinerung
ist Q(n)=D(n)+D(n-1). |
In Worten: Die Summe zweier aufeinander folgender Dreieckszahlen
ist eine Quadratzahl.
... ...... |
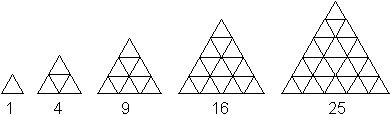Man kann deshalb die Quadratzahlen auch durch eine Folge
von Dreiecken aus Dreiecken illustrieren. |
2
... ... |
Für der Zeichnung gilt Q(5)=9+7+5+3+1. Die Verallgemeinerung
ist Q(n)=1+3+5+...+(2n-1). |
... ... |
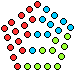Für der Zeichnung gilt F(5)=D(5)+2*D(4). Die Verallgemeinerung
ist F(n)=D(n)+2*D(n-1). |
3
| ...... |
Für der Zeichnung gilt ZS(5)=6*D(4)+1. Die Verallgemeinerung
ist ZS(n)=6*D(n-1)+1. |
4
... ... |
Es ist übrigens möglich, die Formel zu den
zentrierten Sechseckzahlen, nämlich ZS(n)=3n(n+1)+1, über drei
Parallelogramme herzuleiten. |
5
Es folgt noch ein Satz ohne Zeichnung.
Die Summe zweier aufeinander folgender Tetraederzahlen
ist eine quadratische Pyramidenzahl.
Herleitung
T(n)+T(n+1)=n*(n+1)*(n+2)/6 + (n+1)*(n+2)*(n+3)/6 = [(n+1)(n+2)/6]*(n+n+3)=(n+1)(n+2)(2n+3)/6=QP(n+1),
wzbw.
Besondere Dreieckszahlen
top
Es ist eine Spielerei herauszufinden, ob z.B. eine Dreieckszahl
auch in einer anderen Folge der Polygonzahlen vorkommt.
Mit dem Computer fand ich heraus:
Dreieckszahlen
Quadratzahlen
Fünfeckzahlen
Sechseckzahlen
Siebeneckzahlen
Achteckzahlen
...
|
(1/2)n(n+1)
n²
(1/2)n(3n-1)
n(2n-1)
(1/2)n(5n-3)
n(3n-2)
...
|
1 3 6 10 15 21 28...
1 4 9 16 25 36 49...
1 5 12 22 35 51 70...
1 6 15 28 45 66 91...
1 7 18 34 55 81 112...
1 8 21 40 65 96 133...
...
|
Es fällt auf, dass jede
zweite Dreieckszahl auch eine Sechseckzahl ist.
Schreibt man den Term n(2n-1) zu (1/2)n(4n-2) um,
so sieht man deutlicher die Darstellung einer Dreieckszahl mit ungerader
Nummer.
Mehr Zahlen findet man bei
OEIS
OEIS: A001110
These are the numbers that are both triangular and square.
OEIS: A046174
Indices of pentagonal numbers which are also triangular.
OEIS: A046194
Heptagonal triangular numbers.
OEIS: A046181
Indices of octagonal numbers which are also triangular.
Man kann in einer Verallgemeinerung
der Dimension 2 (Dreieckszahlen) auf höhere Dimensionen ausdehnen:
Dreieckszahlen
Tetraederzahlen
Hypertetraederzahlen
...
|
(1/2)n(n+1)
(1/6)n(n+1)(n+2)
(1/24)n(n+1)(n+2)(n+3)
...
|
1 3 6 10 15 21...
1 4 10 20 35 56...
1 5 15 35 70 126...
...
|
Folgen
im pascalschen Dreieck top
Im pascalschen
Dreieck findet man Folgen, die oben als figurierte Zahlen vorgestellt
wurden.
... ... ... |
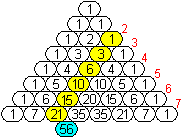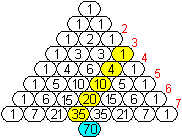In den Spalten stehen Folgen, nämlich
> in der 0.Spalte die stagnierende Folge von Einsen,
> in der 1.Spalte die Folge der natürlichen Zahlen,
> in der 2. Spalte die Folge der Dreieckszahlen,
> in der 3. Spalte die Folge der Tetraederzahlen,
> in der 4. Spalte die Folge der Zahlen
zum 4.dimensionalen Tetraeder,
> in der 5. Spalte die Folge der Zahlen zum 5.dimensionalen
Tetraeder usw. |
Offenbar können Polygon-
und Polyederzahlen auch für höhere Dimensionen definiert werden.
Figurierte
Zahlen im Internet top
Deutsch
georg wengler
Figurierte
oder geometrische Zahlen (.pdf-Datei)
Jutta Gut
Figurierte
Zahlen - die Arithmetik der Spielsteinchen
Martina Schettina
Psephoi
(Zählsteine)
matroid
Figurierte
Zahlen, Pentagon,
Kartenhaus und Summenzerlegung
Wikipedia
Pentatopzahl,
Pyramidenzahl
Englisch
Eric W. Weisstein (MathWorld)
Heptagonal
Triangular Number, Square
Triangular Number, Pentagonal
Triangular Number,
Octagonal
Triangular Number, Rhombic
Dodecahedral Number, Pyramidal
Number
James A. Sellers
Beyond the Basel Problem: Sums
of Reciprocals of Figurate Numbers (.pdf file)
Kate Hobgood and Clay Kitchings (Jim Wilson's Home Page)
Investigating
Figurate Numbers With Technology
OEIS (The On-Line Encyclopedia of Integer Sequences)
Centered
polygonal numbers
Wikipedia
Octagonal
number,
Centered
octagonal number, Nonagonal
number
Referenzen top
(1) F. Ringleb: Mathematische Formelsammlung, Sammlung
Göschen 51, Berlin 1956
(2) Jan Gullberg: Mathematics - From the Birth of Numbers,
New York / London (1997)
[ISBN 0-393-04002-X] Seite 298 ff.
(3) Albert A. Gächter: Figurenzahlen, 2012, www.didamath.com
[ISBN 978- 3 - 9523962-0-9]
Feedback: Emailadresse auf meiner Hauptseite
URL meiner Homepage:
https://www.mathematische-basteleien.de/
© Jürgen Köller
- Juli 2012
top |
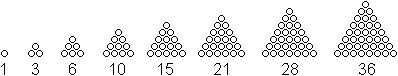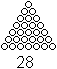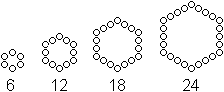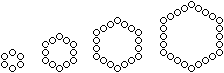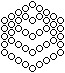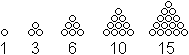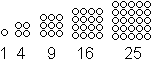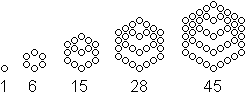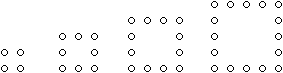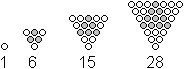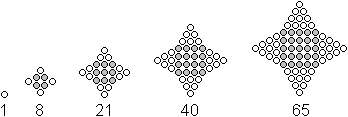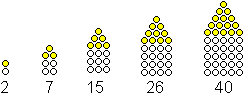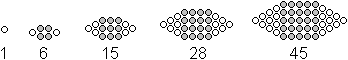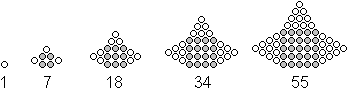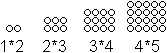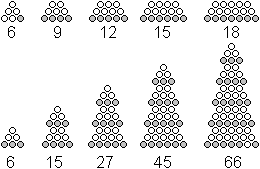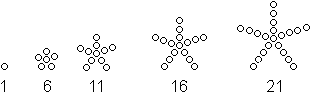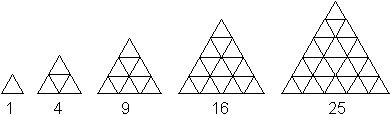