|
Was ist das Pentagondodekaeder?
...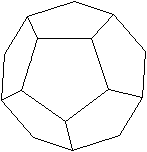 .... .... |
Das Pentagondodekaeder (Kurzform
Dodekaeder) ist ein Körper, der von 12 regelmäßigen
Fünfecken
gebildet wird.
Pentagondodekaeder heißt
Fünfeck-Zwölf-Flächner.
| Das Pentagondodekaeder ist
ein platonischer Körper. |
 |
|
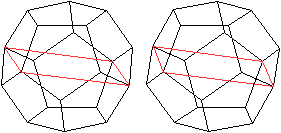
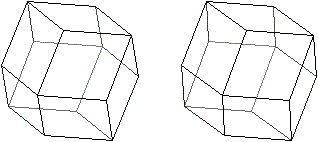
Die folgenden Bildpaare ermöglichen
eine dreidimensionale Sicht des Körpers.
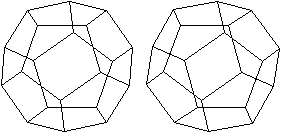
durchsichtig
|
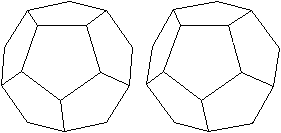
undurchsichtig
|
Im Englischen heißt
der Körper
Regular Dodecahedron, meist abgekürzt als Dodecahedron.
Offensichtlich in Anlehnung daran findet man statt des
Wortungetüms Pentagondodekaeder auch
die Bezeichnung Regelmäßiges Dodekaeder wie z.B. bei
de.wikipedia.
Beschreibungen top
Daten
Das Dodekaeder hat k=30 Kanten, f=12 Flächen und
e=20 Eckpunkte.
Es gilt der eulersche Polyedersatz e+f=k+2.
In jedem Eckpunkt treffen drei Kanten und drei Flächen
aufeinander.
Aufbau
...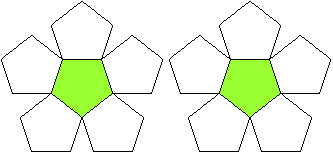 ... ... |
Sechs regelmäßige Fünfecke bilden in
der Ebene eine Rosette.
Klappt man die äußeren Fünfecke nach oben,
so dass sie sich berühren, entsteht eine Schale. |
...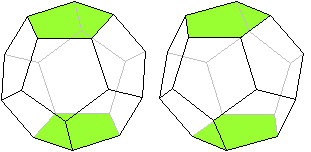 ... ... |
Legt man zwei Schalen verdreht aufeinander, erhält
man das Dodekaeder.
Zwei Fünfecke liegen parallel und sind um 36°
gegeneinander verdreht. Sie bilden die Grundflächen. Dazwischen liegt
im Zickzack ein Band aus zehn Fünfecken. |
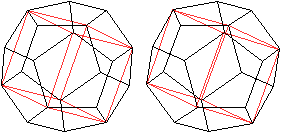
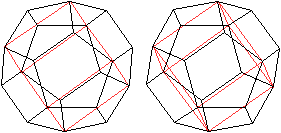
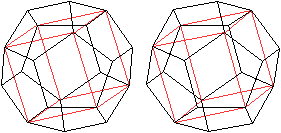
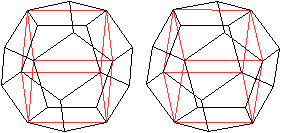
Zwei
Rechtecke
In das Dodekaeder lassen sich wegen
der parallelen Gegenflächen u.a. die folgenden Rechtecke einpassen.
Anzahl
der Raumdiagonalen
...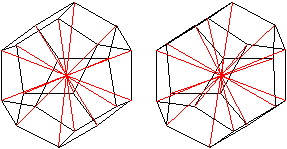 ... ... |
Verbindet man die 20 gegenüberliegenden Eckpunkte,
entstehen 10 Raumdiagonalen.
Sie verlaufen durch den Mittelpunkt des Dodekaeders. |
Es gibt noch zwei Sorten
kürzerer Raumdiagonalen.
...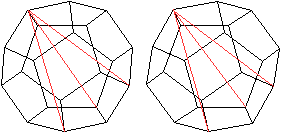 ... ... |
Von einem Punkt gehen 3 Diagonalen einer mittleren Länge
aus.
Da es 20 Ecken gibt, macht das 3*20=60 Diagonalen.
Dabei wird jede Diagonale doppelt gezählt.
Es gibt also 30 Raumdiagonalen dieser Art. |
...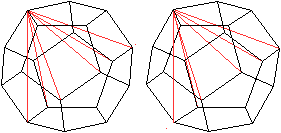 ... ... |
In jedem Punkt beginnen 6 kurze Diagonalen.
Da es 20 Ecken gibt, macht das 6*20=120 Diagonalen.
Dabei wird jede Diagonale doppelt gezählt.
Es gibt also 60 Raumdiagonalen dieser Art. |
Auf die Anzahl 10+30+60=100
Raumdiagonalen kommt man auch auf einem anderen Wege.
Das Dodekaeder hat 20 Eckpunkte.
Verbindet man alle Punkte, so erhält man "20 über
2" oder 190 Linien.
Die Anzahl der Raumdiagonalen ergibt sich, wenn man die
Anzahl der Kanten (30) und die Anzahl der Flächendiagonalen (12*5=60)
abzieht. Das ergibt 100.
Halbierung
des Dodekaeders
...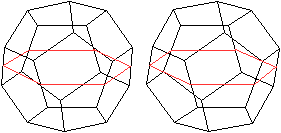 ... ... |
Verbindet man die Mittelpunkte von sechs passenden Kanten,
erhält man ein regelmäßiges Sechseck.
Eine Ebene durch das Sechseck halbiert das Dodekaeder. |
...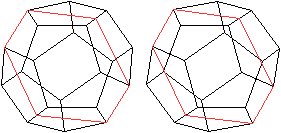 ... ... |
Diese Halbierung ermöglicht einen Zugang zu den
Formeln des Pentagondodekaeders (s.u.). |
Parallelprojektionen
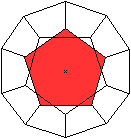
Ein Fünfeck vorne
.
|
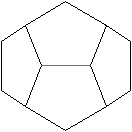
Eine Kante vorne
.
|
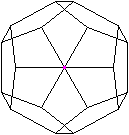
Eine Ecke vorne
.
|
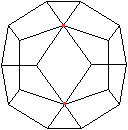
Je zwei Eckpunkte liegen
hintereinander
|
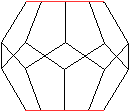
Zwei Gegenflächen werden
zu Strecken
|
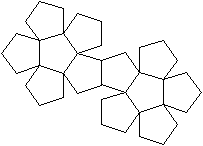
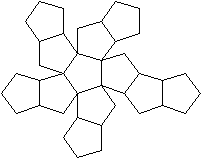
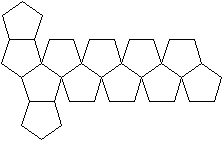
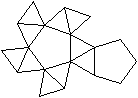
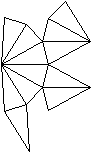
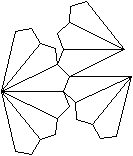
Netze
Das sind drei von 43380 Netzen.
Schlegel-Diagramm
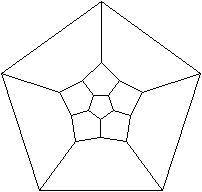
Symmetrien top
Das Dodekaeder hat einen Mittelpunkt.
Er ist das Symmetriezentrum.
... ... ... |
Schaut man auf ein Fünfeck, so stellt sich das Dodekaeder
als eine fünfstrahlige oder fünfzählige, drehsymmetrische
Figur dar.
Die Drehachse ist in der Zeichnung nur ein Punkt. |
...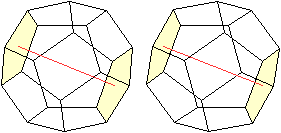 ... ... |
Da es sechs Paare von Fünfecken gibt, gibt es auch
sechs Drehachsen. Sie verlaufen durch die Mittelpunkte der Fünfecke.
Links ein Beispiel |
... ... ... |
Schaut man so auf das Dodekaeder, dass zwei gegenüberliegende
Kanten zusammenfallen, ergibt sich die nebenstehende achsensymmetrische
Figur.
Auf das Dodekaeder übertragen heißt das, dass
eine Ebene durch diese Kanten Symmetrieebene ist. |
...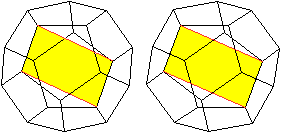 ... ... |
Es gibt 30 Kanten oder 15 Paare von Kanten.
In der linken Zeichnung wird die Symmetrie-Ebene durch
ein Rechteck gekennzeichnet.
Das ist ein Beispiel. |
...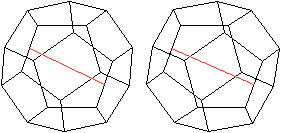 ... ... |
Verbindet man die Mittelpunkte gegenüberliegender
Kanten, so stehen sie für weitere 15 zweistrahlige Achsensymmetrien.
Links ein Beispiel |
... ... ... |
Schaut man auf eine Ecke des Dodekaeders, so stellt es
sich als eine dreistrahlige, drehsymmetrische Figur dar. Diese Symmetrie
überträgt sich auf das Dodekaeder.
Die Drehachse zeigt sich in der Zeichnung als Punkt in
der Mitte. |
..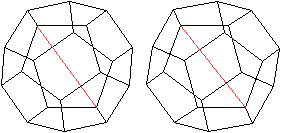 .... .... |
Es gibt 20 Eckpunkte und damit 10 Paare von gegenüberliegenden
Eckpunkten. Durch sie verlaufen die Drehachsen.
Es sind also die längeren Raumdiagonalen.
Links ein Beispiel |
Zusammenfassung: Das Dodekaeder
ist in höchstem Maße symmetrisch.
Es gibt 6+15+10=31 Achsen und 15 Symmetrieebenen.
Ein Würfel
im Dodekaeder
top
Es ist möglich, in ein Dodekaeder
einen Würfel einzuzeichnen, indem man bestimmte Eckpunkte miteinander
verbindet. Dann erscheint das Dodekaeder als ein Würfel, auf dessen
Seitenflächen Walmdächer aufgesetzt sind.
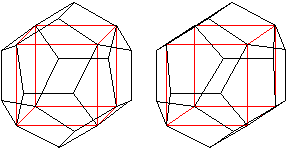
Der Übersichtlichkeit
halber wird nur ein Walmdach eingezeichnet. Von den anderen Dächern
erscheinen nur die Höhe und der First.
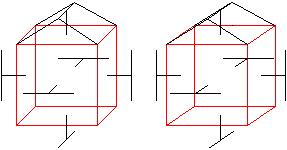
... ... ...
|
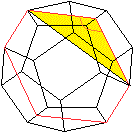
Ein Walmdach besteht aus einem dreiseitigen Prisma und
zwei schiefen Rechteckpyramiden. Die Rechtecke sind gelb gefärbt. |
Unten wird gezeigt, dass man auf diesem Wege das Volumen
des Dodekaeders bestimmen kann.
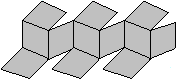
Konkaves
Dodekaeder
...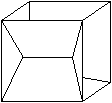 ... ... |
Wenn man einen Würfel vorgibt und die sechs Walmdächer
nach innen richtet, entsteht ein sogenanntes konkaves Dodekaeder.
Will man den dreidimensionalen Raum lückenlos mit
Dodekaeder ausfüllen, so kann man diesen Körper für die
Lücken verwenden. |
Größen top
Das Dodekaeder hat die Kantenlänge a, das
Volumen
V, die Oberfläche O, den Radius R der
Umkugel, den Radius
r der Inkugel und den Radius rkder
Kantenkugel.
Ist die Kantenlänge a gegeben, so gilt für
die übrigen Größen:
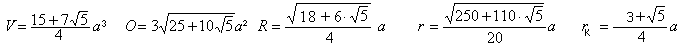
Herleitungen
... ... ...
|
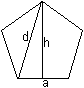
Man verwendet folgende Formeln des regelmäßigen
Fünfecks.
d = (1/2)[1+sqrt(5)]a
h = (1/2)sqrt[5 + 2sqrt(5)]a
[folgt aus d² = h²+(1/4)a²]
rf = (1/10)sqrt[25+10sqrt(5)]a
Af = (1/4)sqrt[25+10sqrt(5)]a² |
Volumen
V
... ... ...
|
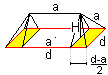
Das Dodekaeder setzt sich aus einem Würfel der Kantenlänge
d und sechs Walmdächern zusammen. Ein Walmdach besteht aus einem Prisma
und zwei schiefen Rechteckpyramiden.
V = d³+6*(1/2)(dH)a+2d(d-a)H
Die Höhe H der Rechteckpyramide wird wie folgt bestimmt: |
... ... ...
|
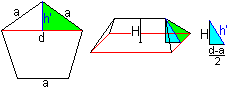
Man benötigt die Dreieckshöhe h', die im regelmäßigen
Fünfeck auftaucht.
Es gilt nach dem Satz des Pythagoras h'² = a²-d²/4.
Weiter ist H² = h'²-(d-a)²/4 = (a²-d²/4)-(d-a)²/4
und
schließlich mit d = [1+sqrt(5)]/2*a die Aussage
H =(1/2)a. |
Man setzt d = [1+sqrt(5)]/2*a
und H = a/2 in die Volumenformel V = d³+6(dH/2)a+12d(d-a)H/3 ein.
Es ergibt sich
V = d³+6*[1+sqrt(5)]/8+12*a³/12 = [15+7sqrt(5)]/4*a³
oder ungefähr V = 7,7a³.
Einfacher kann man das Volumen
wohl über die zwölf fünfseitigen Pyramiden, die durch die
Raumdiagonalen erzeugt werden, bestimmen (s.u.).
Oberfläche
O
O = 12Af = 12*sqrt[25+10sqrt(5)]/4*a²
= 3sqrt[25+10sqrt(5)]a² oder ungefähr O = 20,6a²
Radius
R der Umkugel
... ... ... |
Man legt durch die Mitte des Körpers einen Schnittebene,
in der die Kugeln als Kreise erscheinen. |
...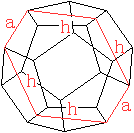 ... ... |
Die Schnittfläche ist ein Sechseck, das aus vier
Fünfeckhöhen und zwei Kanten des Dodekaeders gebildet wird. |
...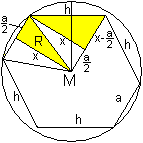 ... ... |
Den Radius R der Umkugel bestimmt man, indem man nach
dem Satz des Pythagoras zunächst die Hilfsstrecke x bestimmt. Es gilt
h²=x²+(x-a/2)². Nach längerer längerer Rechnung
erhält man
x = (1/4)a+(1/4)[sqrt(9+4sqrt(5))]a
= (1/4)a+(1/4)[2+sqrt(5)] = (1/4)a[3+sqrt(5)].
Dann gilt wieder nach dem Satz des Pythagoras R²
= (1/4)a²+x² oder
R = (1/4)sqrt[18+6sqrt(5)]a gerundet 1,4a. |
Radius
r der Inkugel
Man betrachtet wieder das Sechseck,
das das Pentagondodekaeder halbiert.
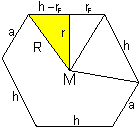 |
Da befindet sich ein rechtwinkliges Dreieck, in dem der
Radius r der Inkugel als Kathete erscheint. Die andere Kathete liegt im
regelmäßigen Fünfeck und ist gleich der Differenz aus seiner
Höhe und seinem Radius des Inkreises. Die Hypotenuse ist R.
Es gilt r² = R²-(h-rF)²
. Nach längerer Rechnung ist r²/a² = (5/8)+(11/40)sqrt(5)
= 250/400+110/400sqrt(5).
Das führt zu r = (1/20)sqrt[250+110sqrt(5)]a. |
Radius
der Kantenkugel
Die Kantenkugel ist die Kugel durch alle Kantenmitten.
...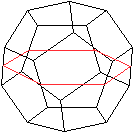 ... ... |
Man erhält den Radius, indem man ein Sechseck des
Dodekaeders, das es halbiert, betrachtet und dann den Umkreis des Sechsecks.
Dessen Radius ist der Radius der Kantenkugel. |
...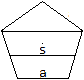 ... ... |
Der Radius ist eine Strecke im Fünfeck. Teilt man
das Fünfeck durch eine Diagonale in ein Dreick und ein Trapez, so
ist die Seite des Sechsecks die Mittellinie im Trapez.
Die Diagonale ist d = (1/2)[1+sqrt(5)]a. Die Mittellinie
ist s = (1/2)(a+d5) = (1/4)[3+sqrt(5)]a.
Der Radius des Umfangskreises eines Sechsecks ist gleich
der Seitenlänge. Damit ist rk = s = (1/4)[3+sqrt(5)]a. |
Winkel
zwischen zwei Fünfeckflächen
... ... ... |
Für die Berechnung des Radius der Umkugel legt man
eine Schnittebene durch das Dodekaeder. Da tritt der gesuchte Winkel alpha
in einem Dreieck an einer Kante auf. Das Dreieck hat als Seiten die Höhen
des Fünfecks und den Abstand gegenüberliegender Kanten. Das sind
h, h und 2rk.
Nach dem Kosinussatz gilt 4rk² = 2h²-2h²cos(alpha).
Dann ist cos(alpha) = (2h²-4rk²)/(2h²).
Setzt man h = (1/2)sqrt[5+2sqrt(5)]a und rk
= (1/4)[3+sqrt(5)]a ein und vereinfacht, so ergibt sich nach längerer
Rechnung cos(alpha) = -(1/5)sqrt(5). Dann ist gerundet alpha = 116,6°. |
Winkel
zwischen Kante und Fünfeckfläche
... ... ... |
Im Sechseck tritt auch der Winkel beta zwischen einer
Kante a und einer Höhe h einer Fünfeckfläche auf und zwar
viermal. Seinen Wert bestimmt man zum Beispiel über die Winkelsumme
im Sechseck, Sie beträgt 4*180°=720°.
Es gilt 4*beta+2*alpha =720°. Daraus folgt beta =(360°-alpha)/2
oder gerundet beta = (360°-116,6°)/2 = 121,7°. |
Mehrere
Würfel im Dodekaeder top
Zwillingswürfel
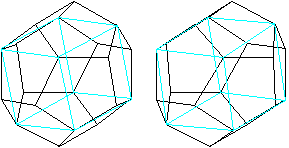
Wie oben erwähnt, ist es möglich, einem Dodekaeder
einen Würfel einzubeschreiben.
Hier sind zwei Würfel dieser Art.
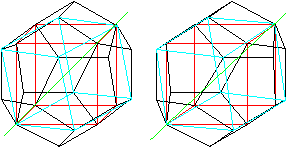
Legt man die Bilder übereinander, so sieht man, dass
die Würfel eine gemeinsame Raumdiagonale (grün) haben und um
diese gegeneinander gedreht sind. In Buch (1) kann man nachlesen, dass
der Drehwinkel 60° beträgt.
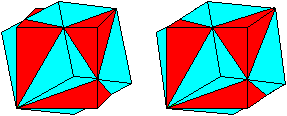
Lässt man das Dodekaeder weg und färbt die
sichtbaren Teile der Würfel unterschiedlich, so entsteht ein Köper,
der nach (2) Seite 455f. twin cube bzw. Zwillingswürfel heißt.
Sternpolyeder
mit 360 Flächen (Cube 5-Compound)
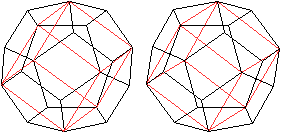
Es gibt fünf Möglichkeiten, einen Würfel
in das Dodekaeder zu legen (1, Seite 103ff.).
...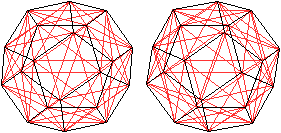 ... ... |
Legt man die fünf Würfel übereinander,
so entsteht ein kompliziert aufgebauter Körper. Man
käme ihm näher, verbände man noch passende Schnittpunkte
miteinander. Selbst dann könnte man sich von ihm wegen der Vielzahl
der Linien kein Bild machen.
Wozu gibt es Computer-Programme? |
...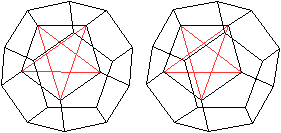 ... ... |
Bei aller Unübersichtlichkeit erkennt man in der
Zeichnung mit allen Würfeln, dass man jede Kante eines Würfels
in der Diagonale eines Fünfecks wiederfindet.
Allgemeiner: Alle Diagonalen der 12 Fünfecke werden
zu einer Kante eines der fünf Würfel. - Die Bilanz stimmt, 5*12=60. |
... ... ... |
Ich empfehle, mit
folgender Grafik zu spielen.
Eric W. Weisstein (Graphics Gallery) Cube 5-Compound
(URL unten)
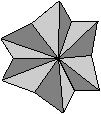
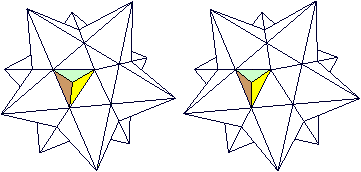
Der Körper aus den fünf Würfeln ist ein
Sternpolyeder mit 30 körperlichen Ecken (Bild), die sich an den Kanten
des Dodekaeders ausbilden. Der Körper hat 30*12= 360 Seitenflächen. |
Es ist bewundernswert zu
lesen, wie Hugo Steinhaus in seinem Buch (1) aus Vor-Computer-Zeiten ein
Bild des Körpers auf sechs Seiten entwickelt.
Bemerkung zum Namen
Den Namen Sternpolyeder mit
360 Flächen habe ich dem Buch (1) entnommen. Das Buch ist eine
Übersetzung aus dem Polnischen. Ich glaube nicht, dass dieser Begriff
die Eigenschaften des Compound erfasst.
Bei en.wikipedia kann man folgende
Beschreibung finden. "Polyhedral compound, a polyhedron composed
of multiple polyhedra sharing the same centre of attention."
Ich kenne keine treffende Übersetzung von Compound.
Weitere
Körper im Dodekaeder top
Tetraeder im Dodekaeder
...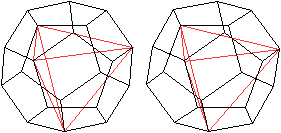 ... ... |
Verbindet man vier passende Eckpunke des Dodekaeders,
so entsteht innen ein Tetraeder.
Insgesamt gibt es 40/4=10 verschiedene Tetraeder. |
Sie bilden zusammen einen
Sternkörper, den Tetrahedron 5-Compound.
Mehr dazu auf meiner Seite Tetraeder.
Antiprisma
im Dodekaeder
...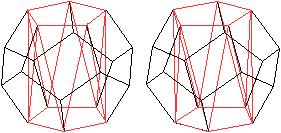 ... ... |
Verbindet man die Eckpunkte gegenüberliegender Fünfecke
durch eine Zickzacklinie, entsteht ein fünfseitiges Antiprisma.
Insgesamt gibt es sechs verschiedene Antiprismen. |
Zwölf
fünfseitige Pyramiden
... ... ... |
Zeichnet man die Diagonalen ein, die durch den Mittelpunkt
des Dodekaeders verlaufen, so erkennt man:
Das Dodekaeder wird von 12 fünfseitigen kongruenten
Pyramiden gebildet, deren Spitzen sich in der Mitte treffen. |
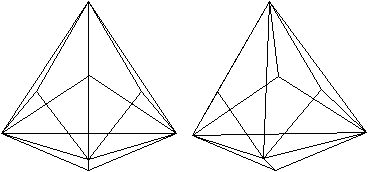
Sechsseitige
Pyramide im Dodekaeder
...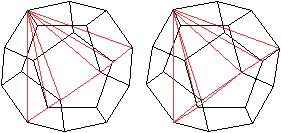 ... ... |
Zeichnet man sechs kurze Raumdiagonalen ein, die von
einem Eckpunkt ausgehen und verbindet die freien, nebeneinanderliegenden
Endpunkte miteinander, entsteht eine gerade Pyramide. Die Grundfläche
ist ein unregelmäßiges Sechseck abwechselnd aus drei Kanten
und drei Flächendiagonalen.
20 Spitzen sind möglich und somit gibt es 20 Pyramiden. |
Ikosaeder
im Dodekaeder
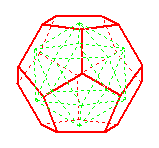
Verbindet man die Mittelpunkte
der Seitenfünfecke eines Dodekaeders,
entsteht ein Ikosaeder.
|
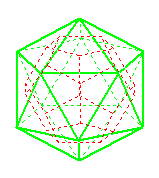
Verbindet man die Mittelpunkte
der Seitendreiecke eines Ikosaeders,
entsteht ein Dodekaeder.
|
Dodekaeder
und Ikosaeder sind duale Körper.
Die beiden letzten Zeichnungen
stellte mir Christian Grünwaldner zur Verfügung.
Vom
Dodekaeder zu weiteren Körpern top
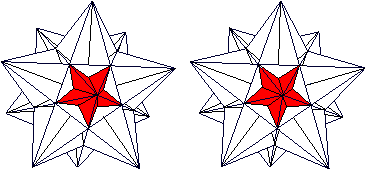
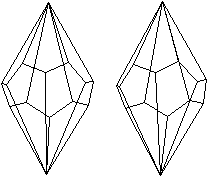
Kleines
Sterndodekaeder
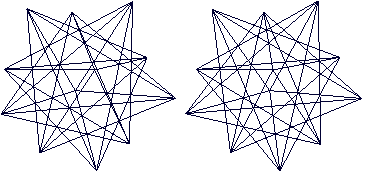
durchsichtig
|
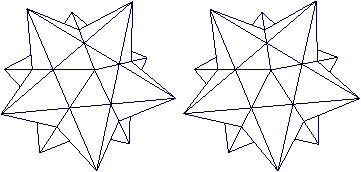
undurchsichtig
|
Vom Kleinen Sterndodekaeder zum Großen
Ikosaeder
Vier
Johnson-Körper
Johnson-Körper
sind konvexe Körper aus verschiedenen regelmäßigen
Vielecken.
Vier (von 92) entstehen aus einem Dodekaeder.
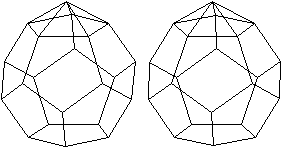
J 58 Erweitertes Dodekaeder
... ... ... |
...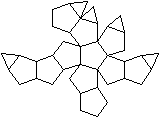 ... ... |
Dem Körper liegt ein Pentagondodekader zugrunde.
Auf eine Seitenflächen wird eine fünfseitige
Pyramide gesetzt. |
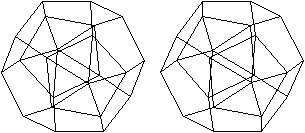
J 59 Doppelt erweitertes
Dodekaeder (para)
... ... ...
|
...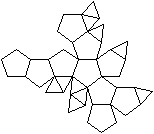 ... ... |
Dem Körper liegt ein Pentagondodekader zugrunde.
Auf zwei gegenüberliegende Seitenflächen wird
eine fünfseitige Pyramide gesetzt. |
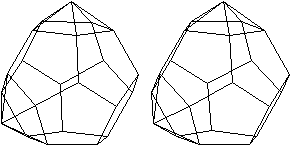
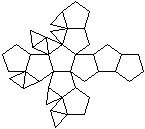
J 60 Doppelt erweitertes
Dodekaeder (meta)
... ... ...
|
... ... ...
|
Dem Körper liegt ein Pentagondodekader zugrunde.
Auf zwei nicht gegenüberliegende Seitenflächen
wird eine fünfseitige Pyramide gesetzt. |
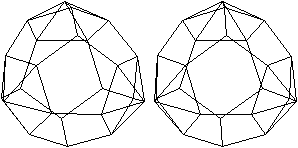
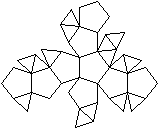
J 61 Dreifach erweitertes Dodekaeder
...  ... ... |
... ...
... |
Dem Körper liegt ein Pentagondodekader zugrunde.
Auf drei Seitenflächen wird eine fünfseitige
Pyramide gesetzt. |
Weitere Dodekaeder
top
Ein Dodekaeder ist ein Zwölfflächner.
Es folgen einige bekannte Körper, die auch von 12
Vielecken gebildet werden.
Es folgen vier Johnson-Körper.
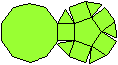
Fünfeckskuppel (J05)

j
|
Verlängerte tetragonale
Bipyramide (J15)
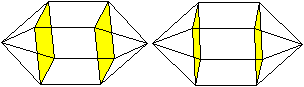
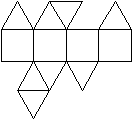
|
Doppelt beschnittenes Ikosaeder (J62)
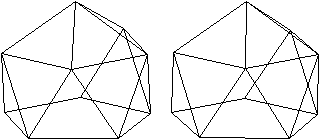
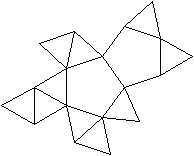
|
Trigondodekaeder (J84)
.
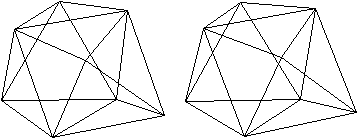
|
Basteleien top
Fünfeckleuchte
... ... ... |
Zu Weihnachten erhielt ich einmal eine Leuchte in Form
eines Dodekaeders. |
...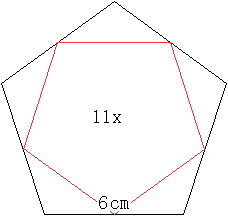 ... ... |
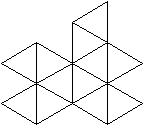
Man stellt die Leuchte aus 11 einzelnen gleichen Fünfecken
aus Karton z.B. der Seitenlänge 6,0 cm her.
Zum Zusammenkleben befinden sich auf den Seiten gleichschenklige
Dreiecke, die durch das Mittenfünfeck entstehen. |
Wie man ein Fünfeck zeichnet, wird auf meiner Seiteregelmäßiges
Fünfeck beschrieben.
... ... ... |
Das Besondere an dieser Leuchte ist, dass sich auf den
Fünfecken durch die Klebflächen ein Sternmuster bildet.
Die Sterne werden sichtbar, wenn man in den oben offenen
Behälter ein brennendes Teelicht stellt. |
Haube

|
Die Gewächshaus-Haube für ein Rundbeet entsteht
in Schweden.
Zur Verfügung gestellt von Bernd Schneider. |
Referenzen top
(1) Hugo Steinhaus: 100 Aufgaben, Leipzig-Jena-Berlin,
1968
(2) Jan Gullberg: Mathematics - From the Birth of Numbers,
New York - London 1997 [ISBN0-393-04002-X]
Pentagondodekaeder
im Internet top
Deutsch
H. B. Meyer (Polyeder aus Flechtstreifen)
Dodekaeder
Gerd Müller
Platonische
Körper in Stereodarstellung
Ingo Roth
Wie erzeuge ich
ein Pentagon-Dodekaeder?
Walter Fendt
Das
Dodekaeder (.pdf-Datei)
Wikipedia
Dodekaeder,
Pentagondodekaeder
(Römer), Trigondodekaeder
Englisch
Eric W. Weisstein (MathWorld)
Dodecahedron,
Cube
5-Compound,
Tetrahedron
5-Compound,
Small
Stellated Dodecahedron
H. B. Meyer (Polyeder aus Flechtstreifen)
Dodecahedron
Marcus Hutter (Marcus' Puzzles Games Pages)
Rubik's
Dodekahedron
Paul Kunkel
The
Dodecahedron
Poly (Pedagoguery Software Inc.)
A program
for downloading (Poly is a shareware program for exploring and constructing
polyhedra)
Die meisten Bilder dieser Seite wurden mit diesem
Programm erzeugt.
Wikipedia
Dodecahedron,
Polyhedral
compound, Snub
disphenoid, Pentagonal
antiprism, Decagonal
prism, Pyritohedron
Französisch
Robert FERRÉOL (MathCurve)
DODÉCAÈDRE
Feedback: Emailadresse auf meiner
Hauptseite
URL meiner Homepage:
https://www.mathematische-basteleien.de/
© 2004,
erweitert 2012, Jürgen Köller
top |


 ....
....


 ...
... ...
...
 ...
... ...
... ...
... ...
... ...
...




 ...
... ...
... ...
... ....
....
 ...
... ...
... ...
... ...
... ...
... ...
...
 ...
... ...
... ...
...
 ...
... ...
... ...
... ...
... ...
... ...
...

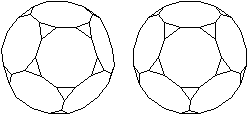
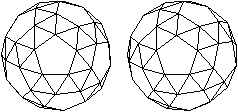
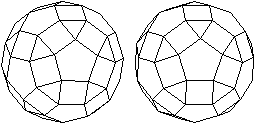


 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
...







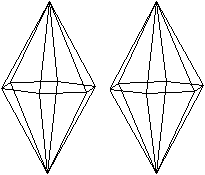
 ...
... ...
... ...
...