|
Was ist Tetra One?
 Tetra One ist nach Cube One
ein weiteres Puzzle des Grafik-Designers, Malers und Zeichners Dieter A.W.
Junker aus Kassel.
Tetra One ist nach Cube One
ein weiteres Puzzle des Grafik-Designers, Malers und Zeichners Dieter A.W.
Junker aus Kassel.
Das Ziel ist es, aus zwei 12-gliedrigen Kaleidozyklen
(Ketten von Dreieckspyramiden) ein Tetraeder zu bauen.
Erste
Beschreibung
top
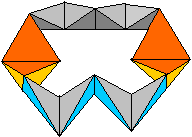
Beide Kaleidozyklen bestehen aus je 12 dreieckigen Pyramiden,
vier großen und acht kleinen. Sie bilden sechs Paare zueinander spiegelbildlicher
Pyramiden.
Die großen Pyramiden sind in Rottönen gehalten,
die kleinen Pyramiden tragen die Farben rot, blau, hell- und dunkelgrau.
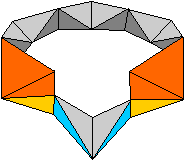
Die beiden Kaleidozyklen unterscheiden sich nur in der
Anordnung der Pyramiden. Einmal liegen zwischen den großen Pyramiden
je vier kleine, einmal sechs und zwei.
Mathematischer
Hintergrund top
Das gelöste Tetraeder zeigt, dass die folgende Aufteilung
des Tetraeders dem Puzzle zugrunde liegt.
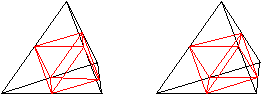
Das Bildpaar ermöglicht eine dreidimensionale Sicht.
Durch die Verbindungslinien der Kantenmitten entstehen
in der Mitte ein Oktaeder und in den vier Ecken vier Tetraeder mit halber
Kantenlänge.
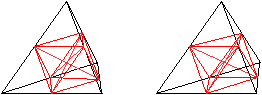 Zeichnet man in das Oktaeder die drei Raumdiagonalen ein,
so ergibt sich eine Aufteilung des Oktaeders in acht Viertelpyramiden.
Zeichnet man in das Oktaeder die drei Raumdiagonalen ein,
so ergibt sich eine Aufteilung des Oktaeders in acht Viertelpyramiden.
Somit ist das Gesamttetraeder in 4+8=12 Pyramiden aufgeteilt.
Bei Tetra One kommt man auf insgesamt 24 Pyramiden, weil jede Pyramide
noch halbiert wird.
Halbierungen
der Dreieckspyramiden top
Ecktetraeder
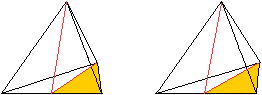 Von einer Kantenmitte aus werden die Verbindungslinien zu
zwei Eckpunkten gezeichnet. Es ergeben sich zwei halb so große Halbtetraeder.
Das gemeinsame Dreieck ist bei Tetra One rot.
Von einer Kantenmitte aus werden die Verbindungslinien zu
zwei Eckpunkten gezeichnet. Es ergeben sich zwei halb so große Halbtetraeder.
Das gemeinsame Dreieck ist bei Tetra One rot.
Viertelpyramiden
Hier ist noch einmal das zentrale Oktaeder in der Aufteilung
in acht Viertelpyramiden.
... ...T ...T |
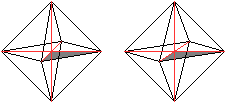
Die Viertelpyramide wird halbiert, indem man wieder von
einer Kantenmitte aus die Verbindungslinien zu zwei Eckpunkten zeichnet.
Es ergeben sich zwei halb so große Achtelpyramiden.
Das gemeinsame Dreieck ist bei Tetra One rot. |
Die oben genannten großen und kleinen Pyramiden der
Kaleidozyklen heißen also treffender Halbtetraeder und Achtelpyramiden.
Netze
top
Das sind die Netze der Pyramiden, die die Ketten bilden.

Halbtetraeder
|
Achtelpyramide
|
Vergleich
der Volumina top
Das Tetraeder
hat allgemein das Volumen VT=(1/12)sqrt(2)a³, das Oktaeder
VO=(1/3)sqrt(2)a³.
Dabei ist a die Kantenlänge
dieser Körper.
Für
das Halbtetraeder heißt das V1=(1/2)(1/12)sqrt(2)(a/2)³=(1/192)a³
Für die Achtelpyramide heißt
das V2=(1/16)(1/3)sqrt(2)(a/2)³=(1/384)a³.
Damit ist das Halbtetraeder doppelt
so groß wie die Achtelpyramide.
Eine
Spitze für Tetra One top
...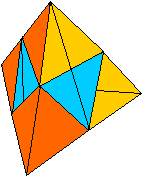 ... ... |
Bei Betrachtung des gelösten Tetraeders fällt
auf, dass die Ecktetraeder und auch die Viertelpyramiden, die außen
blau gefärbt sind, in unregelmäßiger Weise halbiert sind.
Um die Lage der Halbierungslinien besser beschreiben zu
können, soll für
Tetra One eine Spitze definiert werden. |
... ... ... |
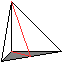
Alle Eckpyramiden sind mit einem Scharnier mit dem Oktaeder
verbunden. Eine Eckpyramide wurde links entfernt. Eingezeichnet ist nur
das Scharnier als rote Strecke. Man kann nun in Pfeilrichtung eine Viertelpyramide
(oder zwei Achtelpyramiden) hochheben. Das ist nur an einer Ecke möglich.
Diese Ecke soll die Spitze von Tetra One sein. |
Lage
der Halbierungen top
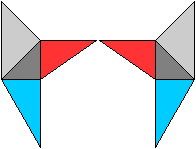
Die Skizze zeigt die Lage der Halbierungslinien der Ecktetraeder.
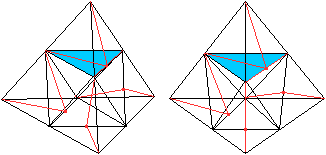 Das blaue Dreieck gehört zum "Deckel", der Viertelpyramide,
die man hochheben kann.
Das blaue Dreieck gehört zum "Deckel", der Viertelpyramide,
die man hochheben kann.
Halbierungslinien der Viertelpyramiden
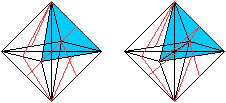 Die Ecktetraeder werden weggelassen.
Die Ecktetraeder werden weggelassen.
Das blaue Dreieck ist wieder der Deckel der Viertelpyramide.
Die roten Linien sind die Halbierungslinien, die man
außen sehen kann.
Lage
des Kaleidozyklus II in Tetra One top
.. .... .... |
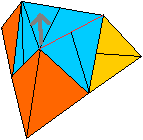
Klappt man die Spitze nach vorne rechts und die Viertelpyramide
nach hinten rechts, so kann man das Kaleidozyklus I herausheben. |
...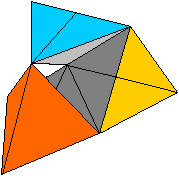 ... ... |
Dann ergibt sich das nebenstehende Bild, wenn man die
obere Viertelpyramide wieder zurückklappt.
So liegt Kaleidozyklus II in Tetra One. |
Vielleicht wird die Lage
dieses Kaleidozyklus deutlicher, wenn man wieder alle Ecktetraeder weglässt
und das Oktaeder in der Aufsicht zeigt.
...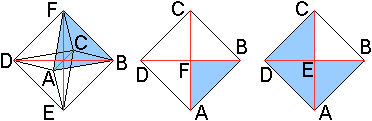 ... ... |
Das Dreieck ABF gehört zum Deckel von Tetra One.
Die restlichen Viertelpyramiden liegen unten wie auch
zwei Ecktetraeder, die hier nicht eingezeichnet sind. |
Kaleidozyklus I ergänzt dann II zu Tetra One.
Viel Spaß beim Lösen von Tetra One. Trotz
meiner Beschreibung bleibt die Lösung eine Herausforderung.

Weitere Puzzles mit Tetraedern findet man auf meiner
Seite Tetraeder-Puzzles.
Tetra
One im Internet top
Dieter A.W. Junker
Flyping Games
(Deutsch/Englisch)
Feedback: Emailadresse
auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2007 Jürgen Köller
top |


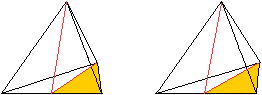






 ...T
...T

 ...
... ...
... ...
...