|
Was ist eine achtstrahlige Figur?
... ... |
Eine achtstrahlige Figur ist eine drehsymmetrische Figur
der Ordnung acht.
Das heißt, dass sie ein Drehzentrum hat und dass
sie bei jeder Achteldrehung um dieses Zentrum in sich selbst übergeht. |
... ...
|
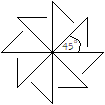In Anlehnung an das Englische nennt man die Drehsymmetrie
auch Rotationssymmetrie.
... ... |
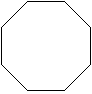Das regemäßige Achteck ist ebenfalls achtstrahlig.
Bei ihm kommen noch 16 Achsensymmetrien hinzu. |
... ...
|
... |
Zu jeder achtstrahligen Figur gibt es ein Spiegelbild.
 |
Diese Seite hat den gleichen
Aufbau wie meine Seiten
Dreistrahlige Figuren,
Vierstrahlige
Figuren, Fünfstrahlige Figuren,
Sechsstrahlige
Figuren. Siebenstrahlige Figuren,
Beispiele
achtstrahliger Figuren top
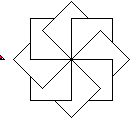
Vorweg: Linien im Achteck
...
... |
Ein Fund im Internet............................................................................................ |
|
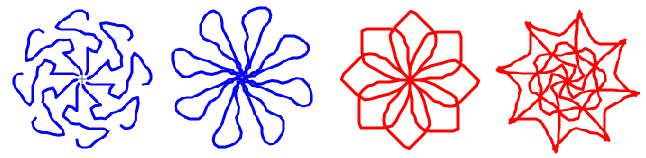Die vier Figuren erzeugte
das Programm Symmetry Artist
der Seite Maths Is Fun (URL unten) |
Epizykloiden top
Eine Herausforderung liegt darin, achtstrahlige Figuren
mit Hilfe von Formeln zu zeichnen.
Da bieten sich die Zykloiden
an.
Epizykloide
... ... |
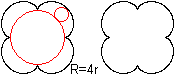Man stelle sich vor, ein Kreis liege fest und ein zweiter
Kreis mit einem viermal so kleinen Radius rolle um einen großen Kreis
(Leitkreis) herum. Verfolgt man dabei einen Punkt auf der Kreislinie des
beweglichen Kreises, so beschreibt er eine geschlossene Linie mit vier
Einkerbungen. Diese Linie heißt Zykloide, genauer Epizykloide. Die
Figur ist vierstrahlig. |
Beschreibt man das Abrollen durch Formeln, so ergibt
sich:
Epizykloide, allgemein
 |
Epizykloide für r=1 und R=8
x(t)=cos(t/8)-a*cos(9t/8)
y(t)=sin(t/8)-a*sin(9t/8)
|
Dabei sind R und r die Radien der Kreise. Die Variable a
gibt die Entfernung des Kurvenpunktes vom Mittelpunkt des beweglichen Kreises
an.
Es folgen Epizykloiden für verschiedene Parameter a.
Gezeichnet mit dem Freeware-Programm Winplot von Richard
Parris (URL unten)
Hypozykloiden
top
... ...
|
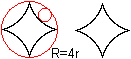Rollt man den kleinen Kreis innen ab, so entsteht eine
Figur mit vier Spitzen, die Hypozykloide. |
Beschreibt man das Abrollen durch Formeln, so ergibt
sich:
Hypozykloide, allgemein
|
Achtstrahlige Hypozykloide
für r=1 und R=8
x(t)=cos(t/8)+a*cos(7t/8)
y(t)=sin(t/8)-a*sin(7t/8)
|
Dabei sind R und r die Radien der Kreise. Die Variable a
gibt die Entfernung des Kurvenpunktes vom Mittelpunkt des beweglichen Kreises
an.
Es folgen Hypozykloiden
für verschiedene Parameter a.
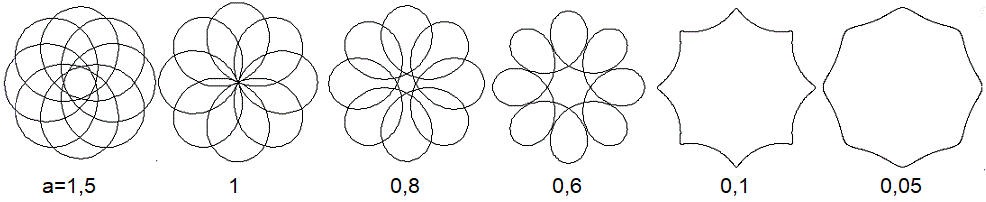
Gezeichnet mit dem Freeware-Programm Winplot von Richard
Parris (URL unten)
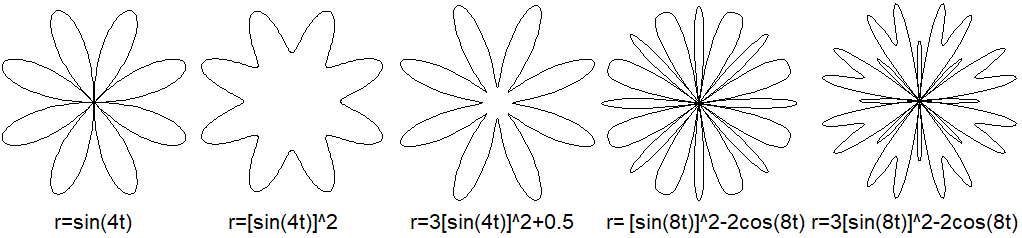
Polargleichungen top
Beispiele
achtstrahliger Körper top
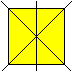
Zur Definition
|
|
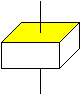
Verschiebt man eine Figur in Normalrichtung, so entsteht
ein Prisma.
Ist die Figur vierstrahlig wie hier das gelbe Quadrat,
so ist auch das Prisma vierstrahlig.
Dabei wird der Drehpunkt durch eine Drehachse ersetzt. |
... ...
|
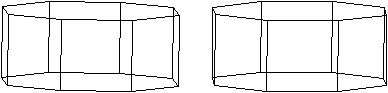
Ersetzt man das Quadrat durch ein regelmäßiges
Achteck, entsteht ein achtseitiges, regelmäßiges Prisma. Die
Gerade durch die Mittelpunkte der Sechsecke ist die Drehachse.
Die Bildpaare ermöglichen ein 3D-Bild. |
... ... |
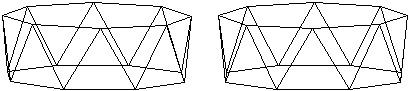Auch das Antiprisma
kann als Grund- und Deckfläche ein regelmäßiges Achteck
haben. Die Seitenflächen sind gleichseitige Dreiecke. |
... ... |
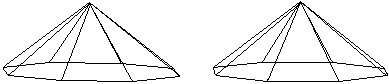Die Gerade achtseitige Pyramide ist achtstrahlig................................................................. |
... |
 |
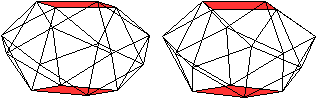
Ferner hat das Abgeschrägte
quadratische Antiprisma
als Parallelprojektion eine achtstrahlige
Figur. |
... |
|
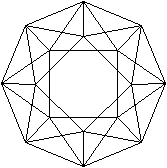
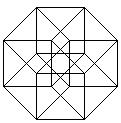
Ein Achteck mit Innenlinien kann
das Bild des vierdimensionalen Würfels, des Hyperwürfels,
sein. |
Vermischtes top
Achtstrahliges aus der Natur
...
Scharbockskraut
|
Mädchenauge
|
Clematis
|
... |
Aus der Werkstatt von Willi Jeschke |
... |
Karen's Quilt.......................................................... |
... ...
Achtstrahlige Blüte von David Collier,
gefaltet von Volker Sayn
|
Achtstrahliger Stern von Tomoko Fuse,
gefaltet von Volker Sayn
|
Hier noch der Hinweis auf
meine Seite Regelmäßiges Achteck.
Achtstrahlige
Figuren im Internet top
Deutsch
Wikipedia
Symmetrie
(Geometrie), Zykloide,
Epizykloiden,
Englisch
Eric W.Weisstein (MathWorld)
Epicycloid,
Hypocycloid
MathsIsFun.com
Symmetry
Artist
Richard Parris (Freeware-Programme)
winplot
Tine Pape (Youtube)
Origami
Kalami Star
Wikipedia
Rotation,
Rotational
symmetry, Rotation
group, Rotation
(mathematics), Epicycloid,
Hypocycloid,
Xah Lee
Epicycloid
and Hypocycloid
Französisch
Robert FERRÉOL
Epitrochoid,
Hypotrochoid
Referenzen top
(1) I.N.Bronstein, K.A.Semendjajew: Taschenbuch der Mathematik,
Leipzig 1987
Feedback: Emailadresse
auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2023 Jürgen Köller
top |
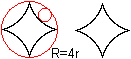