|
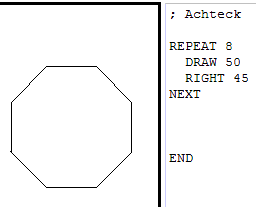
Was ist ein regelmäßiges Achteck?
|
Das regelmäßige Achteck ist ein Vieleck mit
acht gleich langen Seiten und
acht gleich großen Innenwinkeln. |
Das regelmäßige
Achteck heißt nach dem Duden auch Oktogon oder Oktagon.
Auf dieser Seite heißt
es der Einfachheit halber meist nur Achteck.
Eine Formel zum
Achteck top
... ... ...
|
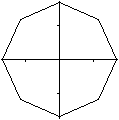
Es ist möglich, ein Achteck in einem Koordinatensystem
durch nur
eine Gleichung zu beschreiben.
2(|x|+|y|)+sqrt(2)(|x-y|+|x+y|)=8
|
Größen
des Achtecks
top
Ist die Seite a gegeben, so lassen sich daraus der Flächeninhalt
A, der Umfang U, der Radius r des Inkreises, der Radius R des Umkreises
und die Längen der Diagonalen d, e und f berechnen.
Es gelten die Formeln:
Herleitung der Formeln
Radius des Umkreises
...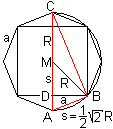 ... ... |
Das Dreieck ABC ist nach dem Satz des Thales ein rechtwinkliges
Dreieck mit der Kathete AB=a, der Hypotenuse AC=2R und dem Hypotenusenabschnitt
AD=R-s. Es gilt der Kathetensatz a²=2R(R-s).
Daraus folgt mit s=sqrt(2)/2*R die Formel R=sqrt[4+2sqrt(2)]/2*a. |
Radius des
Inkreises
|
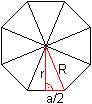
Nach dem Satz des Pythagoras gilt r²=R²-(a/2)².
Daraus folgt r=sqrt[3+2sqrt(2)]/2*a=sqrt[(1+sqrt(2))²]/2*a=(1/2)[sqrt(2)+1]a. |
Flächeninhalt und Umfang
...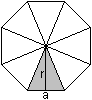 |
A=8[(ar)/2]=2[1+sqrt(2)]a²
U=8a |
Sind die Radien R und r gegeben,
so heißen die Flächenformeln A=2sqrt(2)R² und A=8[sqrt(2)-1]r².
Quelle: (1), Seite 384
Diagonalen
...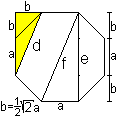 |
Es gilt d²=(a+b)²+b². Daraus folgt d=sqrt[2+sqrt(2)]a.
e=a+2b=[1+sqrt(2)]a
f=2R=sqrt[4+2sqrt(2)]a. |
Winkel
|
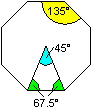
Mittelpunktswinkel: 360°/8=45°
Basiswinkel des Bestimmungsdreiecks des Achtecks: (180°-45°)/2=67,5°
Innenwinkel: 2*67.5°=135° |
Vom Vieleck zum
Achteck top
Das Achteck ist der Sonderfall n=8 des Vielecks.
Kennt man die Formeln des allgemeinen Vielecks, so kann
man die des Achtecks berechnen.
Ist
für ein Vieleck die Seite a gegeben, so gilt
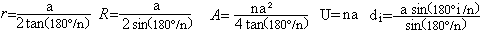
i=1,2,...n-1.
In der Rechnung treten für
n=8 drei Werte trigonometrischer Funktionen auf, nämlich tan(22,5°),
sin(22,5°) und sin(45°).
Es gilt tan(22,5°)=sqrt(2)-1, sin(22,5°)=(1/2)sqrt[2-sqrt(2)]
und sin(45°)=(1/2)sqrt(2).
Damit ergibt sich
r = a/[2tan(22,5°)] = a/[2(sqrt(2)-1)] = (1/2)[sqrt(2)+1]a
R = a/[2sin(22,5°)] =a/sqrt[2-sqrt(2)] =sqrt[2-sqrt(2)]/[2-sqrt(2)]a
= (1/2)sqrt{[2-sqrt(2)][6+4sqrt(2)]}a
= (1/2)sqrt[4+2sqrt(2)]a
A = 8a²/[4tan(22,5°)] = 8a²/[4(sqrt(2)-1)]
= 2[sqrt(2)+1] a²
d2 = d = a sin(45°)/[sin(22,5°)] =
[a(1/2)sqrt(2)]/[(1/2)sqrt[2-sqrt(2)] = ... = sqrt[2+sqrt(2)]a
d3 = e = a sin(67,5°)/[sin(22,5°)]
= a sin(3*22,5°)/[sin(22,5°)]={3sin(22,5°)-4sin³(22,5°]/[sin(22,5°)]}a
= [3-4sin²(22,5°)]a = {3-4(1/4)[2-sqrt(2)]}a
= [sqrt(2)+1]a
d4 = f = a sin(90°)/[sin(22,5°)] =
a/{(1/2)sqrt[2-sqrt(2)]} = ... = sqrt[4+2sqrt(2)]a
Zeichnen eines
Achtecks top
Erste Zeichnung
...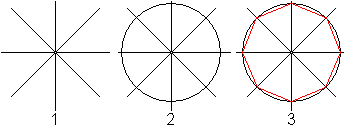 ... ... |
(1) Zeichne eine vertikale und horizontale Gerade und
halbiere die rechten Winkel.
(2) Zeichne einen Kreis um den Schnittpunkt der Geradenkreuzung
mit einem beliebigen Radius.
(3) Verbinde die Schnittpunkte "Kreis/Gerade". |
Die Verbindungslinien sind die Seiten eines Achtecks.
Zweite Zeichnung
...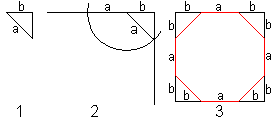 ... ... |
(1) Zeichne ein gleichschenklig-rechtwinkliges Dreieck.
(2) Zeichne einen Kreis um einen Endpunkt der Hypotenuse.
(3) Ergänze die Figur zu einem Quadrat mit der Seitenlänge
b+a+b und zeichne Dreiecke in die drei übrigen Ecken. |
Es entsteht ein Achteck.
Dritte Zeichnung
...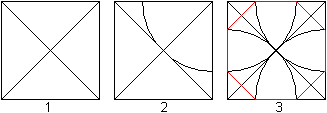 ... ... |
(1) Zeichne ein Quadrat und die beiden Diagonalen.
(2) Zeichne einen Kreis um einen Eckpunkt des Quadrates
mit dem Radius "halbe Diagonale".
(3) Zeichne den gleichen Kreis um die übrigen Eckpunkte
und verbinde entsprechende Schnittpunkte. |
Es entsteht ein Achteck.
Die drei roten Achtecke können
mit Zirkel und Lineal gezeichnet, also konstruiert werden.
Diagonalen im Achteck
top
Das Achteck hat 20 Diagonalen.
...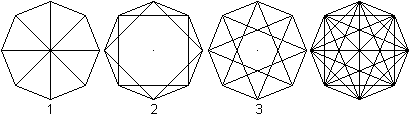 ... ... |
Vier Diagonalen verbinden gegenüberliegende Eckpunkte,
acht jeden zweiten und acht jeden dritten Eckpunkt. |
Achtecke
im Achteck top
...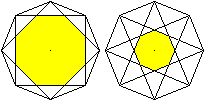 ... ... |
Die kurze und die lange Diagonale erzeugen zwei regelmäßige
Achtecke im Achteck, das große und das kleine Achteck. |
Seitenlänge
des großen Achtecks
...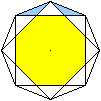 ... ... |
Das obere Dreieck, das durch die kurze Diagonale d vom
Ausgangs-Achteck abgetrennt wird, kann in ein gleichschenklig-rechtwinkliges
und zwei gleichschenklige Dreiecke zerlegt werden. |
...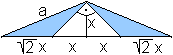 |
Dann gilt d = sqrt(2)x+x+x+sqrt(2)x.
Daraus ergibt sich x=d/[2sqrt(2)+2] = ... = (1/2)sqrt[2-sqrt(2)]a. |
Ergebnis: Die Seitenlänge
des großen Achtecks ist dann 2x = sqrt[2-sqrt(2)]a.
Seitenlänge
des kleinen Achtecks
...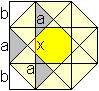 |
Die drei grauen Dreiecke sind kongruent. Ihre Hypotenuse
ist a.
Dann gilt x=(a+2b)-2a = 2b-a = sqrt(2)a-a = [sqrt(2)-1]a,
wzbw. |
Ergebnis: Das innere Achteck
hat die Seitenlänge x=[sqrt(2)-1]a.
Muster im Achteck top

Acht
Achtecke im Achteck
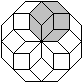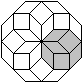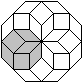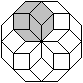
|
Mit Hilfe der 45°-Raute
baut man Achtecke. |
Eine
Spielerei
 |
Die Figur habe ich mehrfach im Internet gefunden.
Das Farbenspiel hat keinen tieferen Sinn, aber System. |
Annäherung an Pi
top
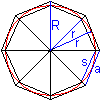
Erste Näherung: Der Kreis
liegt zwischen zwei Achtecken.
|
Umfang des äußeren Achtecks: U=8a
Umfang des inneren Achtecks: u=8s=4sqrt[2+sqrt(2)]a oder
etwa 7,39a
Mittelwert: 7,70a |
Umfang des Kreises:2kr=k[1+sqrt(2)]a oder etwa 2,41ka
Das führt angenähert zu Pi: k=3,20.
Abweichung von Pi: (k-Pi)/Pi=1,9%
Zweite Näherung:
Das lateinisches Kreuz hat einen "Inkreis".
...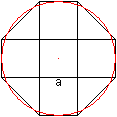 |
Umfang des Kreises: U=2*k*(1.5*a)=3*k*a
Umfang des Achtecks: u=4*a+4*sqrt(2)*a=4*[1+sqrt(2)]*a=9,66*a
Das führt angenähert zu Pi: k=3,22.
Abweichung von Pi: (k-Pi)/Pi=2,5% |
Gleichseitiges
Achteck im Quadrat top
...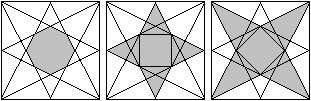 ... ... |
Verbindet man die Seitenmitten eines Quadrats mit den
gegenüberliegenden Eckpunkten, so entstehen ein konvexes Achteck und
zwei vierzackige Sterne, deren Innenfigur Quadrate
sind. |
Gleichseitigkeit
...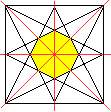 ... ... |
Da die Diagonalen und die Verbindungslinien der Seitenmitten
des Quadrates Symmetrieachsen sind, hat das Achteck gleich lange Seiten. |
Länge
der Seiten
Zur Bestimmung der Seitenlänge AB des Achtecks bestimmt
man die Koordinaten der Punkte A und B.
...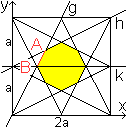 ... ... |
Punkt A ist der Schnittpunkt der Geraden g und h, Punkt
B der von g und k.
g: y=2x und h: y=(1/2)x+a führt zu 2x = (1/2)x+a
oder (3/2)x=a oder xA=(2/3)a. Dann ist yA=(4/3)a.
g: y=2x und k: y=a führt zu xB=(1/2)a
und yB=a. |
AB=sqrt[(xA-xB)²+(yA-yB)²]
= sqrt[(a/6)²+(a/3)²] = sqrt[6a/36)²+(4a/36)²] = sqrt[(5/36)a²]
Dann ist AB=(1/6)sqrt(5)a oder gerundet AB=0,37a.
Innenwinkel
Offenbar ist der Innenwinkel des Achtecks mit dem Scheitelpunkt
A größer als der Innenwinkel mit B.
...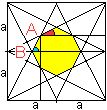 ... ... |
Das zeigt auch die folgende Rechnung.
Der gekennzeichnete rote Winkel ist arc tan(1/2)=26,6°.
Der Innenwinkel ist dann 2*26,6°+90°=143,1°. Der gekennzeichnete
blaue Winkel ist arc tan (2)=63,4°.
Der Innenwinkel bei B ist dann 126,9°. |
Kleiner
Stern
Zur Bestimmung der Seitenlänge AB der Sternfigur
bestimmt man die Koordinaten der Punkte A und B.
...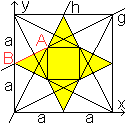 ... ... |
Punkt A ist der Schnittpunkt der Geraden g und h, Punkt
B hat die Darstellung B(0|a).
g: y=(1/2)x+a und h: y=2x führt zu xA=(2/3)a
und yA=(4/3)a.
AB=sqrt[(xA-xB)²+(yA-yB)²]
= sqrt[(4a/9)²+(3a/9)²] = sqrt[(5/9)a²].
Dann ist AB=(1/3)sqrt(5)a oder gerundet AB=0,75a. |
Großer
Stern
...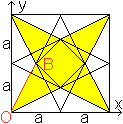 ... ... |
Die Seitenlänge der Sternfigur ist OB.
Der Punkt B die Darstellung B[(1/2)a|a].
Dann ist OB=sqrt[xB²+yB²]
= sqrt[(a/4)²+(a)²] =sqrt[(5a/4)²]=(1/2)sqrt(5)
oder gerundet OB=1,12a. |
Achteckzahlen top

Varianten
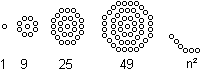
Zentrierte Achteckzahlen
|
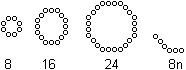
"Achteckrand-Zahlen"
|
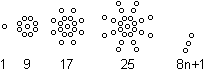
"Achtzackzahlen"
|
Mehr auf meiner Seite Figurierte
Zahlen.
Achtecke aller Art
top
Die folgenden Figuren aus Quadraten und gleichschenklig-rechtwinkligen
Dreiecken sind Achtecke. Sie heißen Polyominos und Polyabolos.

Ein räumliches "Achteck" mit gleich langen Seiten
|

Ein "Achteck" aus acht Halbkreisen
|
... ... ... |
Eigentlich kann auch der Würfel als Achteck bezeichnet
werden, wenn man nur auf die Anzahl der Ecken achtet.
Ein ähnliches Beispiel ist das Oktaeder mit
acht Flächen. |
Parkettierung top
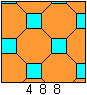
Legt man Achtecke aneinander, so entstehen quadratische
Lücken.
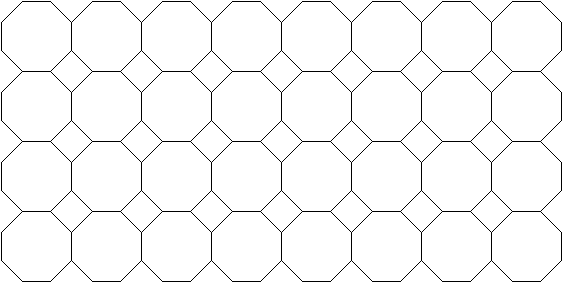
Bei Fußböden sind die Quadrate oft kleiner.

Venedig, Canale Grande 6/2004
Aus der Werkstatt von Willi
Jeschke
Achtecke
in meiner Homepage
top
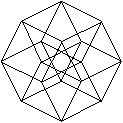
Hyperwürfel
Achtecke mit Innenlinien können
Bilder des vierdimensionalen Würfels, des Hyperwürfels, sein.
Näheres findet man auf meiner Seite über den Hyperwürfel.
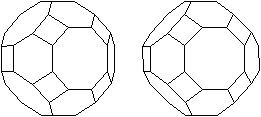
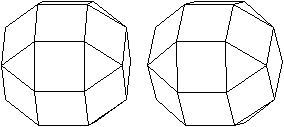
Drei archimedische
Körper
Oktogon top
Ein Oktogon im engeren Sinne ist ein achteckiges Bauwerk.
Meine Auswahl mit Links auf Wikipedia-Seiten
| Baujahr
669 bis 692
798 bis 804
um 1180
1240 bis um 1250
1338-1359
1700 bis 1717
1878
1937
1958-1963
1959-1962
1960-1969 |
Bauwerk
Felsendom
Mittelraum
der Pfalzkapelle Karls des Großen
Turm der Gaukirche
Castel
del Monte
Baptisterium
am Dom
Oktogon
des Herkulesbauwerks
Café
Achteck ;-)
Kirche
auf dem Berg der Seligpreisungen
PanAm Building, jetzt MetLife
Building
Hauptbau der Kaiser-Wilhelm-Gedächtniskirche
Zentralbau der Verkündigungsbasilika |
Ort
Jerusalem, Israel
Aachen, Deutschland
Paderborn, Deutschland
Apulien, Italien
Florenz, Italien
Kassel, Deutschland
Berlin, Deutschland
bei Kapernaum, Israel
New York City, USA
Berlin, Deutschland
Nazareth, Israel |

Kapelle oberhalb des Touristendörfchens
Vitt auf Rügen (1816)
|

Kiosk Oktagon in Berlin-Friedrichshain
Warschauer Straße
|
Warum in die Ferne schweifen?

Das Gartenhaus meines Nachbarn
... ... ... |
Das achteckige Vogelhaus steht in Schweden.
Zur Verfügung gestellt wird es von Bernd Schneider. |
Achteck im Internet
top
Deutsch
Wikipedia
Achteck,
Achterstern,
Oktogon
(Architektur), Rub
al-hizb, Café
Achteck
Englisch
Antonio Gutierrez (GoGeometry)
Problem 287: Regular
Octagon, Diagonals
Eric W. Weisstein (MathWorld)
Octagon,
Octagram,
Star
of Lakshmi, Stomachion
John Page
Octagon
Wikipedia
Octagon,
Octagram,
Octagonal
number,
Centered
octagonal number, Octagon
house, Rub
el Hizb
Referenzen top
(1) H.Kreul [u.a.]: Lehrgang der
Elementarmathematik, Leipzig 1986 [ISBN 3-343-00140-6]
Feedback: Emailadresse
auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2004 (ergänzt 2010) Jürgen Köller
top |






 ...
...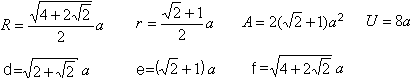
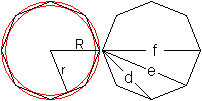
 ...
...



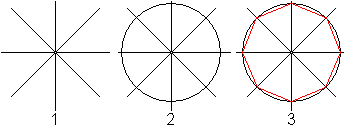 ...
... ...
... ...
... ...
... ...
... ...
...






 ...
... ...
... ...
... ...
... ...
... ...
...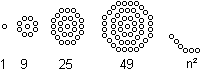
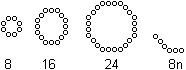
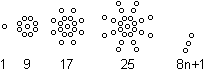


 ...
...
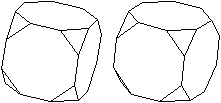


 ...
...