|
Was ist eine Ellipse?
...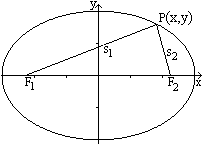 ... ... |
Ein Ellipse besteht aus allen Punkten, deren Summe der
Entfernungen von zwei festen Punkten F1 und F2 gleich
ist.
Die Summe ist in der Zeichnung s1+s2.
Die beiden festen Punkte heißen Brennpunkte. |
Mittelpunktgleichung
top
Mit diesem Ansatz gelangt man zu der "Mittelpunktgleichung"
der Ellipse: x²/a²+y²/b²=1.
Die Variablen a und b stehen für positive reelle
Zahlen.
Herleitung der Mittelpunktgleichung
... .... ....
|
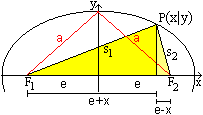
Die Entfernung der Brennpunkte sei 2e und a
sei die Entfernung eines Ellipsenpunktes auf der Mittelsenkrechten der
Brennpunkte von einem Brennpunkt.
Es gilt s1+s2=sqrt[y²+(x+e)²]+sqrt[(y²+(x-e)²]
Ist x=0, so ist s1+s2=2a.
Somit ist sqrt[y²+(x+e)²]+sqrt[(y²+(x-e)²]=2a
die Bestimmungsgleichung der Ellipse. |
Durch zweimaliges Quadrieren werden die Wurzelterme entfernt.
Dabei ist zu beachten, dass Wurzelterme jeweils auf einer Seite der Gleichung
stehen. Die Gleichung heißt dann
a²x²-e²x²+a²y²+a²e²-(a²)²=0
<=> (a²-e²)x²+a²y²=a²(a²-e²)
Führt man die Variable b über b²=a²-e²
ein, so vereinfacht sich die Gleichung zu b²x²+a²y²=a²b²
oder x²/a²+y²/b²=1, wzbw..
Zahlenbeispiel
...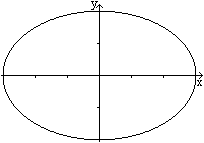 ... ... |
Die Gleichung heißt x²/9+y²/4=1.
Der Definitionsbereich ist Dx={x |-3<=x<=3}
und Dy={y |-2<=x<=+2}.
Es gilt a=3 und b=2. |
Diskussion
der Ellipsengleichung
top
Definitionsbereich
Die Gleichung x²/a²+y²/b²=1 ergibt,
nach y aufgelöst, y=+(b/a)sqrt(a²-x²) und y=-(b/a)sqrt(a²-x²).
Die Relation ist definiert für x²<=a²
oder |x|<=a oder -a<= x <=a, denn für diese Werte ist der
Term a²-x² unter der Wurzel nicht negativ. Die Ungleichung -a<=
x <=a führt zu -b<= y <=b.
So ergibt sich |Dx={x |-a<=x<=a} und
|Dy={y |-b<=x<=+b}.
Deutung
von a und b
...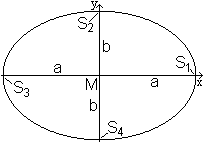 ... ... |
Ist y=0, so ergeben sich aus x²/a²+y²/b²=1
die x-Werte x=a oder x=-a.
Das führt zu den Hauptscheitelpunkten S1(a|0)
und S3(-a|0).
Ist x=0, so ergeben sich aus x²/a²+y²/b²=1
die y-Werte y=b oder y=-b.
Das führt zu den Nebenscheitelpunkten S2(0|b)
undS4(0|-b).
Im Nullpunkt des Koordinatensystems liegt der Mittelpunkt
M der Ellipse.
Die Variable a heißt große Halbachse, die
Variable b kleine Halbachse. |
Zur Entfernung der Brennpunkte 2e
...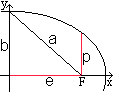 ... ... |
Oben wurde für die Entfernung der Brennpunkte die
Variable 2e eingeführt.
Es gilt b²=a²-e² oder e²=a²-b².
Die Gleichung x²/a²+y²/b²=1 führt
dann für xe=e zu (a²-b²)/a²+y²/b²=1
oder ye=b²/a (oder ye=-b²/a).
Die Strecke ye=b²/a heißt Halbparameter
p der Ellipse. |
Symmetrie
Da die Gleichung x²/a²+y²/b²=1
sich nicht ändert, wenn man x durch -x und/oder y durch -y ersetzt,
ist die Ellipse symmetrisch bezüglich der Achsen.
Ellipsenscharen top
Alle Formen der Ellipse
...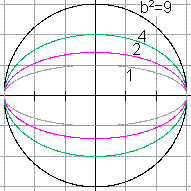 ... ... |
Man erhält alle Formen der Ellipse, wenn man in
x²/a²+y²/b²=1 die Halbachse a festhält und b alle
positiven reellen Zahlen durchlaufen lässt.
Das veranschaulicht die Zeichnung für a=3 und b=1,
sqrt(2), 2 und 3. |
Ist a=b, so artet die Ellipse zu einem Kreis aus.
Alle
Lagen der Ellipse
Wird in einem Koordinatensystem das Symmetriezentrum
nach S(x0|y0) verschoben, so führt das zu den
Gleichungen (x-x0)²/a²+(y-y0)²/b²=1.
Drehungen der Ellipsen werden unten im Kapitel "Ellipse
als Kegelschnitt" angesprochen.
Ellipsen
mit gleichen Brennpunkten
...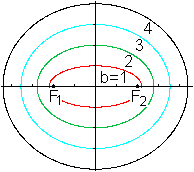 ... ... |
Aus x²/a²+y²/b²=1 wird x²/(e²+b²)+y²/b²=1,
wenn man a²=e²+b² setzt.
In der nebenstehenden Zeichnung ist die Entfernung der
Brennpunkte 2e=4 konstant und für die Halbachse gilt beispielsweise
b=1, 2, 3 und 4.
|
Vier
Scharen von Ellipsen
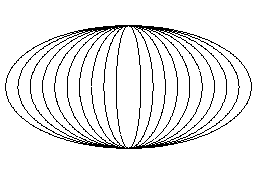
x²/k²+y²/1²=1
|
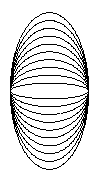
x²/1²+y²/k²=1
|
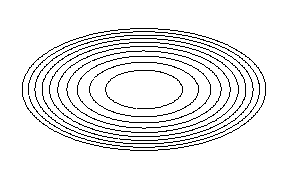
x²/2²+y²/1²=k
|
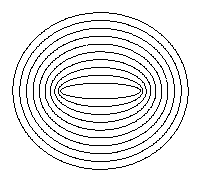
x²/(1+k²)+y²/k²=1
|
Für die Parameterdarstellungen gilt: 0 >= k <=
2 und Schrittlänge 10.
Eine
weitere Definition der Ellipse top
Für die mit der Ellipse verwandte
Parabel gilt der folgende kennzeichnende Satz.
Alle Punkte, die von einer Gerade
l und von einem Punkt F die gleiche Entfernung haben, liegen auf einer
Parabel. Die Gerade heißt Leitlinie und der Punkt Brennpunkt.
Einen
ähnlichen "notwendig und hinreichenden Satz" gibt es auch für
die Ellipse. Da sind die Entfernungen nicht gleich, sondern sie stehen
in einem konstanten Verhältnis zueinander.
...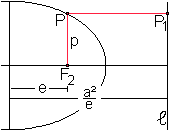 ... ... |
Man zeichnet parallel zur Achse eine Gerade im Abstand
a²/e.
Für den Ellipsenpunkt P(e|p) oberhalb des Brennpunktes
F2 gilt
PP1:PF2= (a²/e-e):p.
Setzt man p=b²/a=(a²-e²)/a, so ist PP1:PF2=a:e. |
...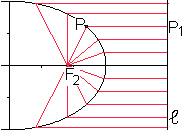 ... ... |
Ist P ein beliebiger Ellipsenpunkt, und verbindet man
ihn mit einem Brennpunkt und zeichnet zu ihm die Senkrechte zur "Leitlinie"
l, so gilt auch PP1:PF2=a:e. |
Herleitung
...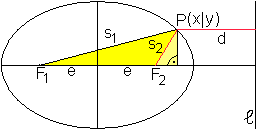 ... ... |
P sei ein beliebiger Ellipsenpunkt. Dann gilt s1+s2=2a.
Nach dem Satz des Pythagoras gilt weiter y²=s1²-(e+x)²
und y²=s2²-(e-x)².
Daraus folgt s1²-(e+x)²=s2²-(e-x)²
oder s1²-s2²=(e+x)²-(e-x)² oder
s1²-s2²=4ex.
Wegen s1²-s2²=(s1+s2)(s1-s2)
und s1+s2=2a ist 2a(s1-s2)=4ex
oder s1-s2=2ex/a. |
Die Gleichungen s1-s2=2ex/a und
s1+s2=2a führen zu x=(a²-s2a)/e.
Für den Abstand des Ellipsenpunktes von der Leitlinie
gilt d=a²/e-x=a²/e-(a²-s2a)/e=as1/e.
Damit ergibt sich die Proportion d:s2=a:e.
Das Verhältnis ist damit unabhängig von der Lage des Ellipsenpunktes
und ist für alle Punkte gleich.
Es lässt sich in der Umkehrung zeigen, dass aus
d/s2=a/e die Gleichung s1+s2=2a folgt.
Folglich könnte man
die Ellipse auch so definieren.
Die Ellipse ist der geometrische Ort aller Punkte, für
die das Verhältnis ihres Abstands d von einer Leitlinie und ihrer
Entfernung s von einem Brennpunkt einen konstanten Wert annimmt.
(5), Seite 329f.
Gerade und Ellipse
top
...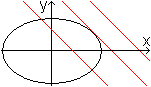 ... ... |
Eine Ellipse und eine Gerade schneiden
sich in zwei Punkten, in einem Punkt oder gar nicht. |
Der Fall eines Schnittpunktes wird weiter verfolgt.
Tangentengleichung
...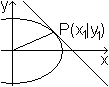 ... ...
|
Lautet die Ellipsengleichung x²/a²+y²/b²=1
und ist der Berührpunkt P(x1| y1),
so ist die Gleichung der Tangente
xx1/a²+yy1/b²=1
|
Herleitung
>Die Ellipsengleichung ist in der Form b²x²+a²y²=a²b²
handlicher.
Die Ableitung beider Seiten ergibt 2b²x+2a²yy'=0
oder nach y' aufgelöst y'=-(b²x)/(a²y).
>Für eine Gerade gilt die Punktrichtungsform (y-y1)/(x-x1)=y'.
Dabei ist P(x1| y1) der Berührpunkt
und y' die Steigung der Ellipse im Punkte P.
>Eine Kombination der Gleichungen führt zur Tangentengleichung
(y-y1)/(x-x1)=-(b²x)/(a²y) und weiter zu
xx1/a²+yy1/b²=1, wzbw..
Ellipse zeichnen top
1.Fall: Gegeben sind die Brennpunkte
der Ellipse und die große Halbachse a.
Fadenkonstruktion
...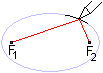 ... ... |
>Befestige die Enden eines Fadens in den Punkten F1
und F2. Der Faden hat die Länge 2a.
>Stecke in die Schlaufe einen Stift und zeichne die Ellipse.
Achte darauf, dass der Faden gespannt ist.
Diese Zeichnung wird durch die Definition der Ellipse
erklärt. |
2.Fall Gegeben sind die Halbachsen
a und b.
Punktweise Konstruktion
...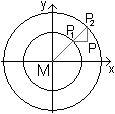 ... ... |
>Zeichne in ein Koordinatensystem zwei konzentrische
Kreise mit den Radien a und b.
Die Mittelpunkte liegen im Nullpunkt des Koordinatensystems
>Zeichne einen Radius des großen Kreises ein. Er
schneidet die Kreise in P1 und P2.
>Zeichne durch P1 eine Horizontale und durch
P2 eine Vertikale.
>Bezeichne den Schnittpunkt dieser Geraden mit Punkt
P. P ist der Punkt einer Ellipse. |
Beweis
...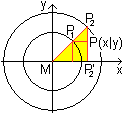 ... ... |
Nach dem ersten Strahlensatz gilt die Proportion P2'P:P2'P2=MP1:MP2.
Darin ist P2'P=y, MP1=b und MP2=a.
Nach dem Satz des Pythagoras ist P2'P2=sqrt(a²-x²).
Das führt zu y:sqrt(a²-x²)=b:a
oder ay=b*sqrt(a²-x²) oder x²/a²+y²/b²=1,
wzbw.. |
Weitere Konstruktionen findet man auf der Webseite der GRAZ-ORTWEINSCHULE
und bei Steven Dutch (URL unten).
Zeichnung
mit Paint
Die meisten Ellipsen auf dieser Seite entstanden mit
Hilfe des Zeichenprogramms Paint. Man findet es bei Windows versteckt mit
dem Pfad Startmenü/Zubehör/Paint.
[Stiftung Warentest bezeichnete es einmal in einem Test
als ein Programm für Vierjährige ;-).]
...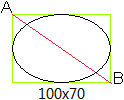 ... ... |
Es soll eine Ellipse mit den Halbachsen a=50 Pixel, b=35
Pixel gezeichnet werden.
>Gehe auf das Feld Ellipse der Toolbox.
>Starte in A und gehe diagonal mit gedrückter Maustaste
auf Punkt B zu.
>Lasse die Maustaste los, wenn auf der Statusleiste unten
rechts 100x70 erscheint.
>Die Ellipse ist fertig. |
Zwei
weitere Formen der Ellipsengleichung top
Parameterform
...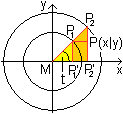 ... ... |
Oben wurde gezeigt, dass man einen Ellipsenpunkt mit
Hilfe zweier konzentrischer Kreise mit den Radien a und b konstruieren
kann.
Führt man den Winkel t ein, wie aus der Zeichnung
zu ersehen, so lassen sich die Koordinaten eines Ellipsenpunktes durch
diesen Winkel und den Halbachsen ausdrücken.
Im Dreieck MP2'P2 gilt x=a*cos(t),
im Dreieck MP1'P1 gilt y=b*sin(t). |
Das ist die Parameterdarstellung der Ellipse: x=a*cos(t)
/\ y=b*sin(t).
Polarform
...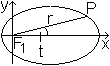 ... ... |
Eine Ellipse wird im allgemeinen durch die Mittelpunktgleichung
x²/a²+y²/b²=1 gegeben. Nun kann man einen Punkt auch
durch seine Entfernung vom Nullpunkt des Koordinatensystems und durch den
Winkel t mit der positiven x-Achse geben. Das sind die Polarkoordinaten. |
Legt man den Nullpunkt in einen Brennpunkt der Ellipse, so
ändert sich die Ellipsengleichung zu (x-e)²/a²+y²/b²=1.
Die Polargleichung ist dann relativ einfach. Sie lautet
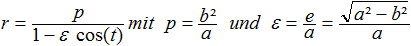 Epsilon heißt die numerische Exzentrizität der
Ellipse. Es gilt epsilon<1.
Epsilon heißt die numerische Exzentrizität der
Ellipse. Es gilt epsilon<1.
Zur Herleitung
Setzt man die beiden Gleichungen x=a*cos(t) /\
y=b*sin(t) der Parameterform in (x-e)²/a²+y²/b²=1,
so erhält man
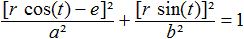 Das ist eine quadratische Gleichung in r. Die positive Lösung
ist die gesuchte Polarform der Ellipsengleichung.
Das ist eine quadratische Gleichung in r. Die positive Lösung
ist die gesuchte Polarform der Ellipsengleichung.
Flächeninhalt
und Umfang
top
Eine Ellipse wird im Allgemeinen durch die beiden Halbachsen
a und b festgelegt.
Dann stellt sich das Problem, aus den beiden Größen
den Flächeninhalt und den Umfang zu berechnen.
Der Flächeninhalt ist
A=pi*ab.
Herleitung
...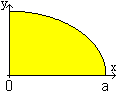 ... ... |
Es genügt, die Viertelellipse im ersten Quadranten
zu betrachten.
Es folgt aus x²/a²+y²/b²=1
die Funktionsgleichung y=(b/a)sqrt(a²-x²). Dann gilt
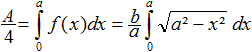
|
Das Integral kann durch die Substitution x=a*sin(t) berechnet
werden.
Es gilt dann sqrt(a²-x²)=a*cos(t) und dx=a*cos(t)dt.
Das führt zu neuen Grenzen: Statt x=0 setzt man
t=0 und statt x=a setzt man t=pi/2 wegen a=a*sin(t) bzw. sin(t)=1.
Für das Intergral heißt das
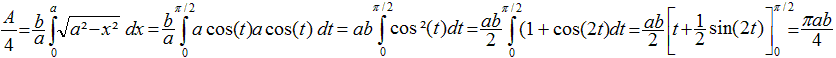 Damit ist A=pi*ab.
Damit ist A=pi*ab.
nach (4), Seite 852f.
Der Umfang
kann nicht durch eine elementare Funktion angegeben werden, nur als "elliptisches"
Integral
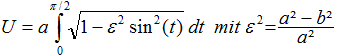 Man kann das Integral näherungsweise über eine
Reihenentwicklung des Integranden bestimmen. Man erhält z.B.
Man kann das Integral näherungsweise über eine
Reihenentwicklung des Integranden bestimmen. Man erhält z.B.
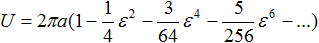
Mehr bei (2), Seite 265
Sammlung
von Aussagen zur Ellipse top
... ... ... |
Eine Ellipse entsteht als Schnittlinie, wenn man durch
einen geraden Kreiszylinder einen schrägen Schnitt legt. |
... ... ... |
Stellt man die Zeichnung auf den Kopf, so bietet sich
die folgende Deutung an.
Ein Kreis wird auf eine schräge Ebene parallel projiziert.
In ihr liegt dann eine Ellipse. |
Mittelpunkte
paralleler Sehnen
...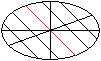 ... ... |
Eine Strecke innerhalb der Ellipse durch den Mittelpunkt
(rot) heißt Durchmesser.
Zeichnet man zu einem Durchmesser die Parallelen, so
liegen die Mittelpunkte der Sehnen auf einem zweiten Durchmesser, dem konjugierten
Durchmesser. |
Mittelpunkte
paralleler Sehnen zum konjugierten Durchmesser
...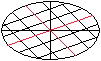 ... ... |
Zeichnet man zum konjugierten Durchmesser wiederum die
Parallelen und halbiert sie, so liegen die Halbierungspunkte wieder den
ursprünglichen Ellipsendurchmesser. |
Zwei Anmerkungen
>Die beiden Achsen der Ellipse sind auch konjugierte
Durchmesser.
>Projiziert man einen Kreis auf eine schiefe Ebene und
erzeugt so eine Ellipse, so werden dabei aufeinander senkrecht stehende
Durchmesser zu konjugierten Durchmessern.
Zwei
Formeln zu konjugierten Durchmessern
...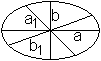 ... ... |
Sind m1 und m2 die Steigungen konjugierter
Durchmesser, so gilt m1m2=-b²/a².
Sind a1und b1 zugeordnete Halbmesser,
so gilt a²+b²=a1²+b1². |
Reflexion
von Brennstrahlen
...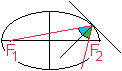 ... ... |
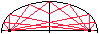
Verbindet man die Brennpunkte der Ellipse mit einem ihrer
Punkte, so entsteht ein Winkel. Dieser Winkel wird von einer Normalen,
einer Senkrechten zur Tangente, halbiert. - So kann ein Flüstergewölbe
wie rechts erklärt werden. Die Köpfe von Sprecher und Hörer
befinden sich in den Brennpunkten. |
... ... ... |
Krümmungskreise
...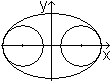 ... ... |
În den Hauptscheitelpunkten der Ellipse links sind
zwei Kreise eingezeichnet, die die Ellipse in diesen Punkten gut annähern.
Die Radien sind r=b²/a. |
Hüllkonstruktion
der Ellipse
...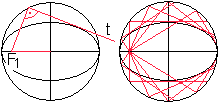 ... ... |
Zeichnet man von einem Brennpunkt der Ellipse aus die
Senkrechte zur Tangente, so liegt der Fußpunkt des Lotes auf dem
Hauptkreis der Ellipse. Das ist der Kreis mit dem Radius a und demselben
Mittelpunkt wie die Ellipse.
Aus diesem Satz folgt die Hüllkonstruktion der Ellipse. |
Größtes
Rechteck in der Ellipse
Passt man in eine Ellipse ein Rechteck
ein, so stellt sich die Frage nach dem größten Rechteck.
...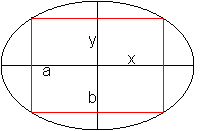 ... ... |
Die Zielfunktion heißt A=4xy oder A²=16x²y².
Die Ellipsengleichung liefert die Nebenbedingung x²/a²+y²/b²=1
oder y²=b²-(b²/a²)x².
Dann ist A²=16x²[b²-(b²/a²)x²]
oder A2=16b2x2-(16b2/a2)x4
Weiter ist die erste Ableitung (A²)'=32b²x-(64b²/a²)x³=32b²x(1-2x²/a²).
(A²)'=0 führt zu 1-2x²/a²=0
oder x²=(1/2)a² oder x=(1/2)sqrt(2)a oder 2x=sqrt(2)a.
Die Gleichung y²=b²-(b²/a²)x²
führt zu y=(1/2)sqrt(2)b odr 2y=sqrt(2)b.
Die zweite Ableitung (A²)''=-4x/a²<0 stellt
sicher, dass das Rechteck wirklich maximal ist. |
Artet die Ellipse zu einem
Kreis aus, gilt also a=b=r, so ist 2x=2y=sqrt(2)r und aus dem maximalen
Rechteck wird ein
Quadrat.
Ellipse als
Kegelschnitt top
Kegelschnitte
...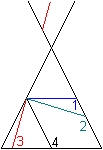 ... ... |
Legt man durch einen geraden Doppelkegel ebene Schnittflächen,
so entstehen im wesentlichen vier Arten von Linien.
1 Ein Schnitt parallel zum Grundkreis führt zum
Kreis.
2 Eine Schnittebene, die den zweiten Einzelkegel nicht
trifft, erzeugt eine Ellipse.
3 Eine Schnittebene, die beide Einzelkegel erreicht,
erzeugt eine Hyperbel.
4 Ein Schnitt parallel zu einer Mantellinie ergibt eine
Parabel.
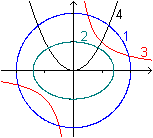
Rechts die vier Linien in der bekannten Darstellung in
einem Koordinatensystem. |
... ... ... |
Scheitelgleichungen
der Kegelschnitte
...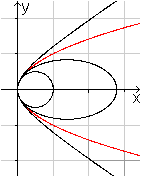 ... ... |
Die Scheitelgleichung für Kegelschnitte lautet:
y²=2px+(epsilon²-1)x²
Es ergeben sich
> der Kreis für epsilon = 0
> die Ellipse für epsilon = 0,8
> die Parabel für epsilon = 1
> die Hyperbel für epsilon = 1,2. |
Quadratische
Gleichung mit zwei Variablen
...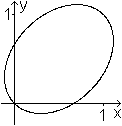 ... ... |
Alle Kegelschnitte erfasst man auch durch die Gleichung
Ax²+Bxy+Cy²+Dx+Ey+F=0.
Eine Ellipse liegt vor, wenn im wesentlichen 4AC-B²>0
ist (3).
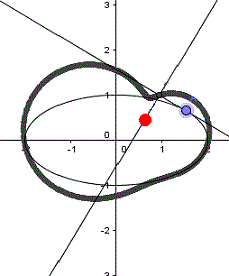
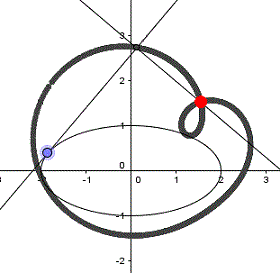
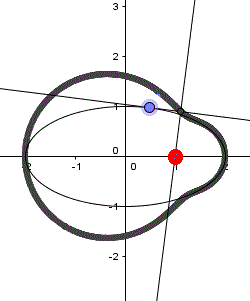
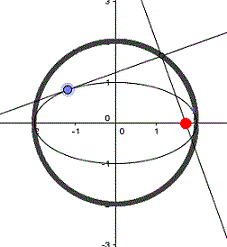
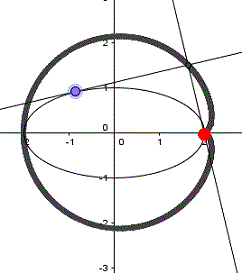
Die nebenstehende Ellipse ist der Graph der Relation 3x²-2xy+3y²-2x-2y=0.
Es ist 4AC-B²=4*3*3-2²=32>0
Offensichtlich bewirkt der Term mit xy eine Neigung der
Symmetrieachsen.
Quelle: (2) Aufgabe 991a |
Kurven zur Ellipsetop
Fußpunktkurven
Mehr auf meiner Seite Fußpunktkurve
Evolute
...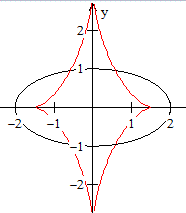 ... ... |
Eine Evolute ist der geometrische Ort der Mittelpunkte
der Krümmungskreise einer Kurve.
Die Evolute der Ellipse mit x²/4+y²/1=1 ist
die Astroide mit x(t) = (3/2) cos³(t) und y(t)
= -3 sin³(t). |
Mehr auf meiner Webseite Evolute
Ellipsen im Internet
top
Deutsch
Wikipedia
Ellipse,
Rotationsellipsoid,
Flüstergewölbe,
Superellipse,
Superformel,
Krümmungskreis,
Englisch
Gary S. Stoudt (Convergence MAA)
Can
You Really Derive Conic Formulae from a Cone?
Eric W. Weisstein (MathWorld)
Ellipse,
Ellipsoid,
One-Seventh
Ellipse, Curvature,
Circumellipse,
Steiner
Circumellipse
John J O'Connor and Edmund F Robertson (The MacTutor History
of Mathematics archive)
Ellipse
Richard Parris (Freeware-Programme)
winplot
Xah Lee
Ellipse
Wikipedia
Ellipse,
Ellipsoid,
Whispering
gallery, Superellipse,
Superformula,
Osculating
circle
Französisch
Robert FERRÉOL (mathcurve)
Ellipse
Referenzen top
(1) Otto Zoll: Mathematisches Lehr- und Arbeitsbuch für
höhere Lehranstalten, Oberstufe, Braunschweig 1940
(2) Autorengemeinschaft: Algebra und Geometrie
für Ingenieure, Frankfurt/M Zürich 1966 [ISBN 978-3-87144-107-3]
(3) I.N.Bronstein, K.A.Semendjajew: Taschenbuch der Mathematik,
Leipzig 1987
(4) Jan Gullberg: Mathematics - From the Birth of Numbers,
New York - London 1997 (ISBN0-393-04002-X)
(5) W.Gellert (Herausgeber u.a.): Kleine Enzyklopädie
Mathematik, Leipzig 1986
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
http://www.mathematische-basteleien.de/
©
2007 Jürgen Köller
top |
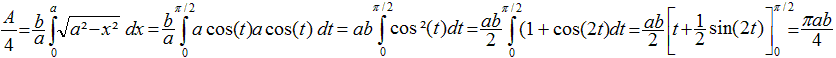
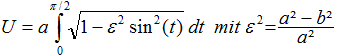

 ...
... ....
.... ...
... ...
... ...
... ...
... ...
...



 ...
... ...
... ...
... ...
...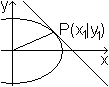 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
...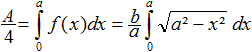
 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
...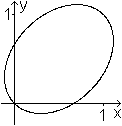 ...
...
 ...
...