|
Was ist eine Parabel?
...... ... ... |
Eine Parabel ist eine mathematische Kurve............................................................................. |
...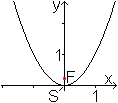 ... ... |
Man erhält eine einfache Parabel, die Normalparabel,
als Graph der quadratischen Funktion mit f(x)=x².
Wie alle Parabeln ist sie achsensymmetrisch, hat einen
Scheitelpunkt S und einen Brennpunkt F. |
Für diese Seite habe
ich Bekanntes zur Parabel ausgewählt und knapp beschrieben.
Parabelschar
top
...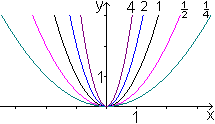 ... ... |
Man erhält alle Formen der Parabel, wenn die Variable
a alle positiven reellen Zahlen in der Funktionsgleichung f(x)=ax²
durchläuft.
In der Zeichnung sind es stellvertretend fünf Zahlen. |
So wie die Kreise sind alle Parabeln ähnlich, wenn es
auch nicht so aussieht.
Zwei Figuren sind ähnlich, wenn sie durch eine einfache
Verkleinerung oder Vergrößerung ineinander übergeführt
werden können. Das erreicht man durch eine Maßstabsänderung.
Man wählt x=(1/a)X und y=(1/a)Y. Dann wird
y=ax² zu (1/a)Y=a[(1/a)X]² oder Y=X².
Aus jeder Parabel kann also eine Normalparabel werden.
(4)
Scheitelform
top
...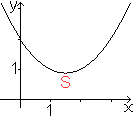 ... ... |
Verallgemeinert man f(x)=ax² zur Gleichung einer
quadratischen Funktion f(x)=ax²+bx+c, so liegt der Scheitelpunkt nicht
mehr unbedingt im Nullpunkt.
Die nebenstehende Parabel wird durch die Gleichung f(x)=0,5x²-1,5x+2
beschrieben. |
Mit Hilfe der "quadratischen
Ergänzung" kann man die Gleichung so umformen, dass man die Lage des
Scheitelpunktes erkennt.
f(x)=ax²+bx+c (allgemeine Form)
<=> f(x)=a[x²+(b/a)x]+c
<=> f(x)=a{x²+(b/a)x+[b/(2a)]²}-[b²/(4a)]+c
<=> f(x)=a[x+b/(2a)]²-[b²/(4a)]+c (Scheitelform)
Der Scheitel liegt an der Stelle xs=-b/(2a).
Dann ist f(xs)=c-b²/(4a).
Sind a=0,5 und b=-1,5 und c=2, so sind xs=1,5
und ys=0,875. Das bestätigt die Zeichnung oben.
Neben der Scheitelform gibt
es noch die Produktform f(x)=a(x-x1)(x-x2), die in
dieser Form nur existiert, wenn die Parabel die x-Achse an zwei Stellen
schneidet, nämlich in x1 und in x2.
Steigungsproblem
top
...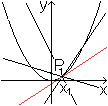 ... ... |
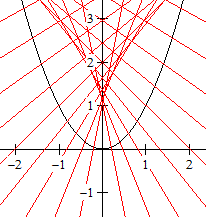
Zeichnet man durch den Punkt P1 der Normalparabel
mit f(x)=x² Geraden, so schneiden sie die Parabel im allgemeinen in
zwei Punkten. Es gibt aber eine Grenzlage, in der eine Gerade nur einen
Punkt mit der Parabel gemeinsam hat. Das ist die rote Gerade, die auf einer
Seite der Parabel liegt und die sie im Punkte P1 berührt.
Diese Gerade heißt Tangente. |
Es stellt sich die Frage, in welcher Weise die Steigung der
Tangente von der Stelle x1 abhängt.
...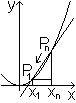 ... ... |
Zur Bestimmung betrachtet man einen Punkt Pn,
der sich auf P1 zu bewegt, und gleichzeitig die Steigung der
Sekante PnP1.
| In Formelsprache sieht das so aus: |
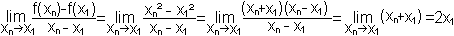 |
|
Durch den Trick mit der dritten binomischen Formel kann man
ein Produkt erzeugen und dann kürzen, so dass der Grenzwert problemlos
gebildet werden kann.
Ergebnis: Die Parabel hat an der Stelle x1
die Steigung 2x1.
In diesen Überlegungen
liegt eine Bedeutung der Parabel: Sie gestattet einen einfachen Zugang
zur Differentialrechnung.
Flächenproblem
top
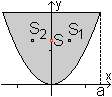
Es geht um das Problem, den (gelben) Flächeninhalt
eines Flächenstückes zu berechnen, das von der Parabel und einer
Schnittgeraden begrenzt wird.
...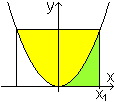 ... ... |
Im hier gewählten einfachen Fall ist die Parabel
eine Normalparabel mit f(x)=x².
Die Schnittgerade ist die Horizontale y=x1².
Man bestimmt der Einfachheit halber zunächst den
grünen Flächeninhalt unter der Parabel, der rechts von x=x1
begrenzt wird. |
...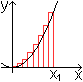 ... ...
|
Dazu zeichnet man n Streifen der Breite x1/n
und zunehmender Höhe, die die Parabel überdecken.
Der Flächeninhalt dieser Treppenfläche ist
An=(x1/n)(1*x1/n)²+(x1/n)(2*x1/n)²+(x1/n)(3*x1/n)²+...+(x1/n)[n*x1/n)]²
=[1²+2²+3²+...+n²]/n³*x1³=[(1/6)n(n+1)(2n+1)]/n³*x1³=[(1/6)(1+1/n)(2+1/n)]x1³. |
Lässt man die Anzahl n der Streifen gegen Unendlich
gehen und somit die Streifenbreite gegen Null, so geht An gegen
(1/3)x1³. Das ist der Flächeninhalt unter der Parabel.
Für das Parabelsegment
ist dann A=(2x1)x1²-(2/3)x1³=(4/3)x1³.
In der Rechnung wird die
Formel 1²+2²+3²+...+n²=(1/6)n(n+1)(2n+1) verwendet.
In diesen Überlegungen
liegt eine weitere Bedeutung der Parabel:
Sie gestattet einen einfachen Zugang zur Integralrechnung.
...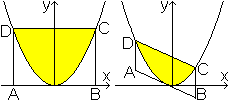 ... ...
|
Im Bronstein (5) findet man den folgenden Satz.
Der Flächeninhalt des Parabelsegments verhält
sich zum Flächeninhalt des Parallelogramms wie 2 zu 3.
Ist das Parallelogramm ein Rechteck wie ganz links, so
ist der Satz durch die obige Rechnung erklärt. |
Figuren im
Parabelsegment
top
...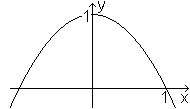 ... ... |
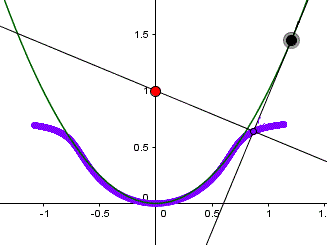
Man erhält ein Parabelsegment wie links, indem man
die Normalparabel an der x-Achse spiegelt und um eine Einheit nach oben
verschiebt. Das führt zur Funktionsgleichung mit f(x)=-x²+1.
Es soll untersucht werden, welche Abmessungen einige
Figuren im Parabelsegment mit einem festen oder maximalen Flächeninhalt. |
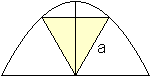
Gleichseitiges Dreieck
a=sqrt(7)-sqrt(3)
|
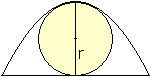
Kreis
r=1/2
|
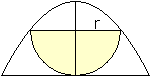
Halbkreis
r=(1/2)[sqrt(5)-1]
|
Die
roten Figuren haben einen maximalen Flächeninhalt.
Rechteck
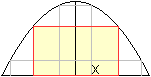 |
Ansatz: A=2xy
Nebenbedingung: y=-x²+1
Zielfunktion: A(x)=2x(-x²+1)=-2x³+2x
A'(x)=-6x²+2, A''(x)=-12x. A'(x)=0 führt zu
-6x²+2=0 oder x²=1/3 oder x=(1/3)sqrt(3) und y=2/3. |
Das maximale Rechteck hat die Maße 2x=(2/3)sqrt(3)
LE und y=2/3 LE.
Gleichschenkliges Dreieck
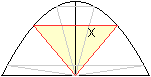 |
Ansatz: A=(1/2)2xy=xy
Rechnung wie beim Rechteck
Lösung: x=(1/3)sqrt(3) und y=2/3 |
Das maximale Dreieck hat die Maße 2x=(2/3)sqrt(3) LE
und y=2/3 LE.
Gleichschenkliges Trapez
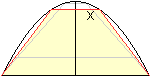 |
Ansatz: A=(1/2)(2+2x)y=(1+x)y
Nebenbedingung: y=-x²+1
Zielfunktion: A(x)=(x+1)(-x²+1) oder A(x)==-x³+x-x²+1
A'(x)=-3x²-2x+1. A'(x)=0 führt zu x²+(2/3)x-1/3=0
oder x=1/3 und dann y=8/9. |
Das maximale Trapez hat die Grundseiten 2 LE, 2/3 LE und
die Höhe 8/9 LE.
Rechtwinkliges Dreieck
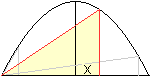 |
Ansatz: A=(1/2)(1+x)y
Rechnung wie beim gleichschenkligen Trapez.
Lösung: x=1/3 und y=8/9 |
Das maximale Dreieck hat die Katheten 4/3 LE und 8/9 LE.
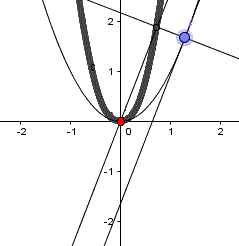
Parabelsegment
Für welchen Parameter a ist der Flächeninhalt
des rot gekennzeichneten Parabelsegments maximal?
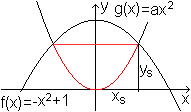 |
Schnittpunkt der beiden Parabeln
Ansatz: ax²=-x²+1
Dann ist (a+1)x²=1 oder x²=1/(a+1) und xs=sqrt[1/(a+1)]=(a+1)-1/2.
Weiter ist ys=1-1/(a+1)=a/(a+1). |
Für die Fläche (1/2)A(a) gilt
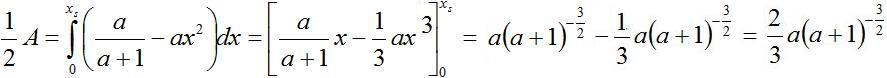
Dann ist nach der Produktregel die Ableitung
(3/4)A'(a) wie folgt.
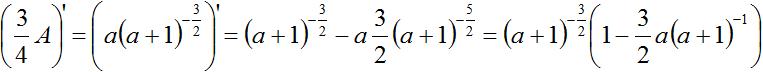
[(3/4)A]'=0 führt zu 1-(3/2)a/(a+1)=0 oder 2(a+1)=3a
oder a=2.
Lösung: Die Fläche ist maximal für a=2.
Wurzelfunktion top
...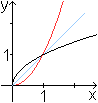 ... ... |
Spiegelt man den roten Parabel-Ast an der ersten Winkelhalbierenden,
so ergibt sich der Graph einer Wurzelfunktion. Sie ist die Umkehrfunktion
von f(x)=x² für x>=0.
Aus y=x²folgt nämlich
x=sqrt(y) oder nach Vertauschen von x und y die Gleichung der Wurzelfunktion
y=sqrt(x). |
Parabel als Ortslinie
top
...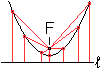 ... ... |
Gegeben sind die Gerade l und der Punkt F.
Dann gilt:
Alle Punkte, die den gleichen Abstand von der Gerade
l und die gleiche Entfernung vom Punkt F haben, liegen auf einer Parabel.
Die Gerade heißt Leitlinie und der Punkt Brennpunkt (Fokus). |
Beweis:
...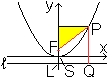 ... ...
|
Die Kurve ist wirklich eine Parabel, wie die folgende
Rechnung zeigt.
Vorweg: Es sei LS=SF=p/2.
Dann gilt FP=PQ oder sqrt[(y-p/2)²+x²]=y+p/2
oder x²=2py oder y=[1/(2p)]x².
Die Gleichung y=[1/(2p)]x² beschreibt eine
Parabel. |
...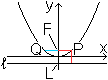 ... ... |
Die Strecke LF=p heißt Parameter.
Die horizontal liegende Sehne QP durch den Brennpunkt
hat die Länge 2p und gibt die "Breite" der Parabel an. |
Satz von den Sehnen
top
..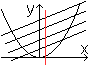 .... .... |
Zeichnet man parallele Sehnen der Parabel und ermittelt
deren Mittelpunkte, so liegen sie auf einer Parallelen zur y-Achse.
Diese Parallele heißt auch Durchmesser der Parabel. |
Beweis:
Man bestimmt die Schnittpunkte der Parabel y=[1/(2p)]x²
mit einer Geraden y=mx+b.
Aus [1/(2p)]x² = mx+b folgt die quadratische Gleichung
x²-2pmx-2pb=0 mit den Lösungen x1=pm+sqrt(p²m²+2pb)
und x2=pm-sqrt(p²m²+2pb). Es gilt dann (x1+x2)/2=pm.
Der Term pm ist konstant. Die Gerade x=pm
ist eine Parallele zur y-Achse.
Über Tangenten top
Gleichung der Tangente
|
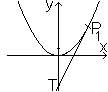
Die Tangente durch den Punkt P1(x1|y1)
der Parabel mit f(x)=1/(2p)x² hat die Steigung f '(x1)=(1/p)x1.
Die Punktsteigungsform der Geradengleichung lautet (y-y1)/(x-x1)=f
'(x1).
Dann ist die Gleichung der Tangente y=(x1/p)x+y1. |
Raute
...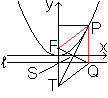 ... ... |
Greift man die Figur der Parabel als Ortslinie noch einmal
auf, so kann man sie so ergänzen, dass eine Raute entsteht.
Es gilt PQ parallel FT. Dann gilt weiter neben
PQ=FP
auch FT=PQ. Nach der Tangentengleichung ist nämlich FT=y1+p/2.
Das gilt auch für PQ. Damit ist das Viereck TQPF eine Raute. |
Die Raute führt zu folgenden Aussagen.
>Die Parabeltangente halbiert den Winkel zwischen Brennstrahl
PF und Leitstrahl PQ.
>Die Tangente liegt in Richtung der Diagonale einer Raute.
Die andere Diagonale verläuft durch den Brennpunkt. Das führt
zur Hüllkonstruktion der Parabel im nächsten Kapitel.
Parabolspiegel
...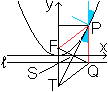 ... ... |
Die eingezeichnete Senkrechte zur Tangente kann als Einfallslot
eines Lichtstrahls gedeutet werde, der vom Brennpunkt F ausgeht und in
P unter dem gleichen Winkel reflektiert wird. Stellt man sich die Figur
noch dreidimensional vor, hat man einen Parabolspiegel vor sich. Da der
Lichtweg umkehrbar ist, zeigt die Figur auch, dass achsenparallele Strahlen
im Brennpunkt zusammentreffen. So erklärt sich der Name Brennpunkt. |
 |
Parabeln zeichnen top
Schablone
...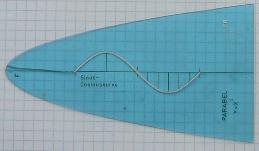 ... ... |
Man verwendet zum schnellen Zeichnen der Normalparabel
eine Schablone, die meist praktischerweise auch die Sinuskurve enthält.
Die Einheit ist 1cm. |
Fadenkonstruktion
...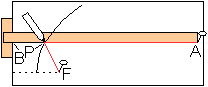 ... ... |
In dieser Fadenkonstruktion wird die Definition der Parabel
als Ortslinie verwendet. Man stellt ein Reißbrett und eine Reißschiene
bereit. Ein Faden der Länge AB wird an einem Ende an der Schiene in
A befestigt, am anderen Ende in Punkt F. Fährt man eine Bleistiftspitze
an der Reißschiene entlang bei gespanntem Faden, so entsteht eine
Parabel. |
Es gilt AP+PB=PF+PA. Daraus folgt PF=PB. Die linke Kante
des Reißbrettes ist die Leitlinie, der Punkt F Brennpunkt.
Hüllkonstruktion
... ... ... |
...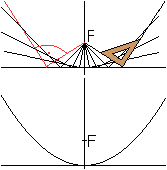 ... ... |
Die Parabel kann als Einhüllende von Tangenten ermittelt
werden.
Das ergibt sich aus den Diagonalen der Raute (s.o.) |
Parabel
als Graph einer Relation top
...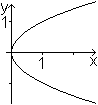 ... ... |
Bei dieser Lage der Normalparabel ist die x-Achse jetzt
ihre Symmetrieachse.
Die y- und die x-Achse sind ausgetauscht. Die Gleichung
ist jetzt y²=x.
Die Parabel ist jetzt nicht mehr der Graph einer Funktion,
sondern einer Relation. Bei einer Funktion verlangt man, dass jedem
x-Wert genau ein y-Wert zugeordnet ist. Hier gehören zu jedem x-Wert
zwei y-Werte. Diese Relation ist nur noch für positive reelle Zahlen
einschließlich 0 erklärt. |
Die Gleichung kann zu y²=2px (Scheitelgleichung) und
weiter zu ay²+by+c=x verallgemeinert werden.
In dieser Form wird die Parabel in der Analytischen Geometrie
als Kegelschnitt behandelt.
Parabel als
Kegelschnitt top
Kegelschnitte
...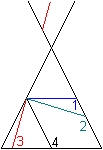 ... ... |
Legt man durch einen geraden Doppelkegel ebene Schnittflächen,
so entstehen im wesentlichen vier Arten von Linien.
1 Ein Schnitt parallel zum Grundkreis führt zum
Kreis.
2 Eine Schnittebene, die den zweiten Einzelkegel nicht
trifft, erzeugt eine Ellipse.
3 Eine Schnittebene, die beide Einzelkegel erreicht,
erzeugt eine Hyperbel.
4 Ein Schnitt parallel zu einer Mantellinie ergibt eine
Parabel.
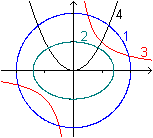
Rechts die vier Linien in der bekannten Darstellung in
einem Koordinatensystem. |
 |
Parabel
als Kegelschnitt
Die Parabel wird etwas genauer
untersucht.
... ... ...
|
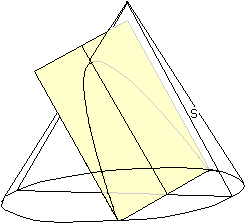
Schrägbild eines parabolischen Kegelschnitts.
Die Schnittebene liegt parallel zu einer Mantellinie s.
Legt die Schnittebene etwas flacher, ergibt sich eine
Ellipse. So kann die Parabel als Grenzlinie einer Ellipse angesehen werde.
Der eine Scheitel ist sichtbar, der andere liegt "im Unendlichen". |
Zum
Beweis
...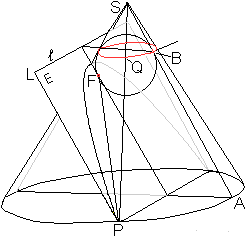 ... ... |
Zum Nachweis, dass die Schnittlinie eine Parabel ist,
legt man in den Kegel eine sogenannte Dandelinsche Kugel so, dass sie den
Kegel im roten Kreis und die Ebene in Punkt F berührt. Die Ebene,
in der der rote Kreis liegt, schneidet die Ebene, in der die Parabel liegt,
in der Geraden l.
Ist P ein beliebiger Punkt der Parabel, so kann gezeigt
werden, dass er gleich weit von Punkt F und von der Schnittgeraden l entfernt
ist.
Nach einer oben dargestellten Überlegung ist das
eine kennzeichnende Eigenschaft der Parabel. Die Gerade heißt wie
oben Leitlinie l und der Punkt Brennpunkt F. |
|
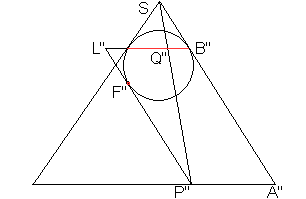
Links der Aufriss des Kegelschnitts. Er ist so angelegt,
dass PL=P''L'' gilt.
Es gilt der Reihe nach
1. PF=PQ
2. PQ=AB
3. A''B''=P''L''=PL
4. PQ=AB=A''B''
Danach ist PL=PF, wzbw. |
(1)
Scheitelgleichungen
der Kegelschnitte
|
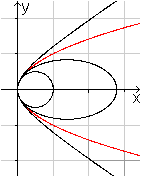
Die Scheitelgleichung für Kegelschnitte lautet:
y²=2px+(epsilon²-1)x²
Es ergeben sich
> der Kreis für epsilon = 0
> die Ellipse für epsilon = 0,8
> die Parabel für epsilon = 1
> die Hyperbel für epsilon = 1,2. |
Quadratische
Gleichung in zwei Variablen
... ... ...
|
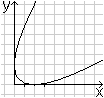
Alle Kegelschnitte erfasst man auch durch die Gleichung
Ax²+Bxy+Cy²+Dx+Ey+F=0.
Eine Parabel liegt vor, wenn im wesentlichen 4AC-B²=0
ist (3).
Die nebenstehende Parabel ist der Graph der Relation
x²-2xy+y²-4x-4y+4=0. Offensichtlich bewirkt der Term xy eine
Neigung der Symmetrieachse. |
Delisches
Problem (Problem der Würfelverdoppelung) top
Der Sage nach sollten die Griechen
nach einer Antwort des Orakels auf Delos von der Pest befreit werden,
wenn sie den würfelförmigen Altar des Apollo doppelt so groß
machten. (Dieses ist eine Version der Geschichte.)
...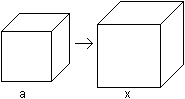 ... ... |
Das Problem der Würfelverdoppelung
führt mit dem Ansatz 2a³=x³ zur Lösung x=a*2^(1/3).
Für die Griechen galt dies nicht als Lösung, denn die Strecke
x musste nur mit Zirkel und Lineal aus der Strecke a ermittelt werden.
Man weiß heute, dass diese Aufgabe unlösbar ist, denn nur Terme
mit Quadratwurzeln sind konstruierbar. Kreise und Geraden führen nämlich
zu linearen und quadratischen Gleichungen, zu denen x³=2a³ nicht
gehört. |
... ... ... |
Der griechische Mathematiker Menaechmus (um 380–ca. 320
v. Chr., er lebte unter Alexander dem Großen) beschäftigte sich
mit Kegelschnitten.
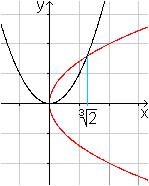
In diesem Zusammenhang gab er eine Lösung des Delischen
Problems mit Hilfe des Schnittpunktes zweier Parabeln an.
Wählt man y² = 2x and y = x², so hat der
Schnittpunkt die Abszisse x=2^(1/3). |
Polargleichung
der Parabel
top
An Stelle der Koordinaten x und y wird die Lage eines
Punktes durch die Entfernung r vom Nullpunkt und dem Winkel zwischen r
und der positiven Richtung der x-Achse beschrieben. Es gilt x=r*cos(phi)
und y=r*sin(phi).
...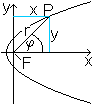 ... ... |
Die Polargleichung wird einfach, wenn man den Brennpunkt
als Nullpunkt des Koordinatensystems wählt. Die Parabelgleichung heißt
dann y²=2p(x+p/2). Man ersetzt x und y und erhält r²*sin²(phi)=2p[r*cos(phi)+p/2].
Das ist eine quadratische Gleichung in r. Löst man sie in einer längeren
Rechnung, so ist die positive Lösung r=p/[1-cos(phi)] die gesuchte
Polargleichung.
Der Definitionsbereich ist D={phi| 0<phi<360°}. |
Mehr über Parabeln
top
Potenzfunktionen
...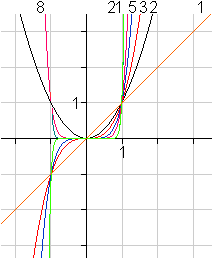 ... ... |
Bisher waren Parabeln immer das Bild quadratischer Gleichungen.
Man bezeichnet die Graphen von Potenzfunktionen n-ter
Ordnung mit f(x)=xn
(n ist eine natürliche Zahl) auch als
Parabeln, und zwar als Parabeln n-ter Ordnung.
Links Graphen für n=1, 2, 3, 5, 8, 21.
Für n=3 ergeben sich kubische
Parabeln, die allgemeiner durch y=ax³ (a ungleich 0) beschrieben
werden.
Nur die Parabeln zweiter Ordnung haben einen Brennpunkt
und eine Leitlinie. |
Neilsche
Parabeln (Semikubische Parabeln)
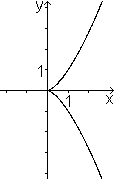
|
Die Gleichung y²-ax³=0 ( a ungleich 0) beschreibt
die neilschen Parabeln.
Das Aussehen links erhält man für a=1.
Im ersten Quadranten ähnelt sie dem Parabel-Ast der
Normalparabel.
Darauf weist die Umwandlung der Gleichung y²=x³
in y=x1,5 hin. |
Evolute
der Parabel
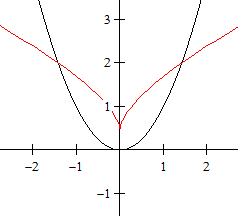 |
Eine Evolute ist der geometrische
Ort der Mittelpunkte der Krümmungskreise einer Kurve.
Die Evolute der Normalparabel ist die neilsche Parabel
mit der Gleichung (27/16)x² = (y-1/2)³. |
Fußpunktkurven
Näheres auf meiner Webseite Fußpunktkurven
Kettenlinie
(Katenoide)
Die Kettenlinie wird leicht mit der Parabel verwechselt.
Zum Beispiel das halbe Logo von McDonald's , viele Brückenbögen
und der Gateway Arch von St. Louis sind Kettenlinien und keine Parabeln.
... ... ... |
Man erhält eine Kettenlinie, wenn man zum Beispiel
wie links eine Uhrenkette an den Enden aufhängt und frei hängen
lässt.
Dahinter steht die Funktionsgleichung f(x)=(ex+e-x)/2
oder f(x)=cosh(x). |
...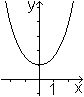 ... ... |
Es gibt bei mir eine Webseite über die Kettenlinie.
Ich verweise noch auf zwei weitere Webseiten.
Parabeln im Internet
top
Deutsch
Arndt Brünner
Quadratische
Funktion durch 3 Punkte finden
Matroids Matheplanet
Zur
Scheitelbestimmung bei quadratischen Funktionen
Wikipedia
Parabel
(Mathematik), Quadratische
Funktion, Quadratische
Gleichung, Parabelschablone
Englisch
Alexander Bogomolny (Cut-the-Knot)
Two
Tangents to Parabola, Parabolic
Mirror, Parabola
as envelope of lines, Reflective
properties of parabola
Eric W. Weisstein (MathWorld)
Parabola,
Conic
Section,
Parabola
Evolute,
Paraboloid,
Semicubical
Parabola
Gary S. Stoudt (The Mathematical Association of America)
Can
You Really Derive Conic Formulae from a Cone? (Apollonius, Conics,
Book I, Proposition 11)
JOC/EFR/BS (The MacTutor History of Mathematics archive)
Parabola
Richard Parris (Freeware-Programme)
winplot
Wikipedia
Parabola,
Parabolic
reflector,
Conic
section
Xah Lee
Parabola,
Conic
Sections
Französisch
Robert FERRÉOL (mathcurve)
Parabole,
CHAÎNETTE
Referenzen top
(1) Otto Zoll: Mathematisches Lehr- und Arbeitsbuch für
höhere
Lehranstalten, Oberstufe, Braunschweig 1940
(2) Martin Gardner: Geometrie mit Taxis, die Koepfe der
Hydra und andere mathematische Spielereien, Basel 1997
(3) Autorengemeinschaft: Algebra und Geometrie
für Ingenieure, Frankfurt/M Zürich 1966 [ISBN 978-3-87144-107-3]
(4) Rademacher Toeplitz: Von Zahlen und Figuren, Berlin
Heidelberg New York, 1968 [ISBN 3-540-04190-7]
(5) I.N.Bronstein, K.A.Semendjajew: Taschenbuch der Mathematik,
Leipzig 1987
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2007 Jürgen Köller
top |
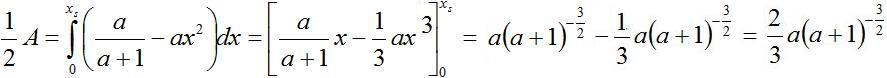
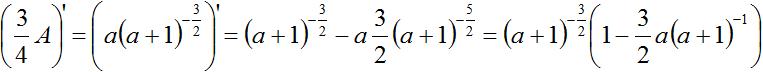
 ...
...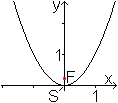 ...
... ...
... ...
... ...
...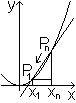 ...
... ...
... ...
...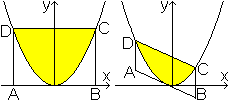 ...
... ...
...






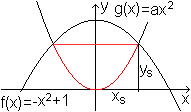
 ...
... ...
...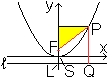 ...
... ...
... ....
....
 ...
... ...
...
 ...
... ...
... ...
...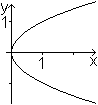 ...
... ...
...
 ...
... ...
...

 ...
... ...
... ...
...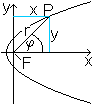 ...
... ...
...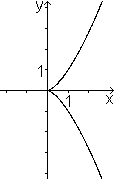

 ...
...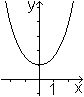 ...
...