|
Was ist ein Kreisausschnitt?
...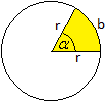 ... ... |
Zeichnet man in einen Kreis mit dem Radius r zwei Radien
ein, so begrenzen sie und der Kreisbogen b ein Flächenstück.
Das ist der Kreisausschnitt oder der Kreissektor. - Nennt man den Winkel
zwischen den Radien alpha, so entsteht ferner ein zweiter Kreisausschnitt
mit dem Winkel 360°-alpha und dem Kreisbogen 2pi*r-b. Er wird auf dieser
Webseite nicht untersucht. |
Größen
des Kreisausschnitts top
...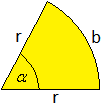 ... ... |
Offenbar ist der Kreisausschnitt durch den Radius r und
den "Mittelpunktswinkel" alpha eindeutig bestimmt. Aus diesen beiden Größen
lassen sich die Kreisbogenlänge b und der Flächeninhalt A berechnen. |
Kreisbogenlänge
b
Offenbar sind die Kreisbogenlänge b und der Winkel
alpha proportional.
Es gilt b:alpha = (2pi*r):360°. Dann ist b = (pi*r)(alpha/180°).
Flächeninhalt
A
Offenbar sind der Flächeninhalt A und der
Winkel alpha proportional.
Es gilt A:alpha = (pi*r²):360°. Dann ist A
= (pi*r²)(alpha/360°).
Ist der Winkel im Bogenmaß
gegeben, werden die Formeln einfacher.
Kreisbogenlänge b
Es gilt b:alpha = (2pi*r):(2pi rad). Dann ist b = r(alpha/rad)
oder b = rx.
Es ist üblich, alpha durch die Variable x zu ersetzen,
wenn der Winkel im Bogenmaß angegeben wird. Dann erübrigt sich
der Zusatz rad.
Flächeninhalt A
Es gilt A:alpha = (pi*r²):(2pi rad). Dann ist A
= (1/2)r²(alpha/rad) oder A= (1/2)r²x.
Zahlenbeispiel
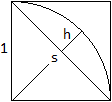
Gegeben: r=1 cm, alpha = 90°. Gesucht:
A, b
.... .. .. |
b = (pi*r)(alpha/180°) = (pi*1 cm)(90°/180°)
= (1/2)pi cm oder ungefähr 1,6 cm
A = (pi*r²)(alpha/360°) = (pi*1
cm²)(90°/360°) = (1/4)pi cm² oder ungefähr 0,8 cm² |
Kreisabschnitt top
Sehne s und Höhe h
...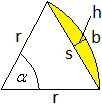 ... ... |
Zeichnet man in den Kreisausschnitt die Sehne s ein,
so wird er aufgeteilt in einen Kreisabschnitt oder Kreissegment und in
ein gleichschenkliges Dreieck.
Der Kreisabschnitt ist gekennzeichnet durch die Sehne
s, die die Grundseite bildet, und die Höhe h. Beide Längen lassen
sich aus den Grundgrößen Radius und Mittelpunktswinkel alpha
wie folgt berechnen. |
...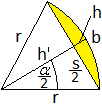 ... ... |
Für die Sehne s gilt sin(alpha/2) = s/(2r) oder
s
= 2r*sin(alpha/2).
Die Höhe im Dreieck sei h'. Es gilt cos(alpha/2)
= h'/r oder h' = r*cos(alpha/2) und damit h = r-h'= r-rcos(alpha/2)
oder h = [1-cos(alpha/2)]r. |
Flächeninhalt
Aab
...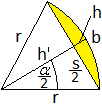 ... ... |
Für die Berechnung des Flächeninhalts
des Kreisabschnittes benötigt man den Flächeninhalt des Dreiecks.
Es gilt Adr = (1/2)h's
= (1/2)[r*cos(alpha/2)][2r*sin(alpha/2)] = r²*sin(alpha/2)*cos(alpha/2)
= (1/2)r²sin(alpha). |
Der Flächeninhalt Aab
des Kreisabschnitts ergibt sich aus Aab = A-Adr.
Das heißt Aab =(pi*r²)(alpha/360°)-(1/2)r²sin(alpha)
oder Aab = [pi*(alpha/360°)-(1/2)sin(alpha)]r².
Ist der Winkel im Bogenmaß
gegeben, so lauten die Formeln wie folgt.
s = 2r*sin(alpha/2) oder s = 2r*sin(x/2)
h = [1-cos(alpha/2)]r oder h = r[1-cos(x/2)].
Aab = [pi*(alpha/360°)-(1/2)sin(alpha)]r²
oder Aab = (1/2)r²[x-(1/2)sin(x)]
Zahlenbeispiel
Gegeben: r=1 cm, alpha = 90°. Gesucht:
s, h, Aab
... ... ... |
s = 2r*sin(alpha/2) = 2sin(45°) cm = sqrt(2)
cm oder ungefähr 1,4 cm
h = [1-cos(alpha/2)]r = [1-(1/2)sqrt(2)]cm = (1/2)[2-sqrt(2)]cm
oder ungefähr 0,3 cm |
Aab = [pi*(alpha/360°)-(1/2)sin(alpha)]r²
= [(1/4)pi-(1/2)]cm² oder ungefähr 0,3 cm².
In-
und Umkreis des Kreisausschnitts top
...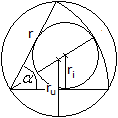 ... ... |
Der Kreisausschnitt hat einen Inkreis und einen Umkreis.
Wie groß sind die Radien ru und ri der beiden
Kreise, wenn der Kreisausschnitt durch den Radius r und den Mittelpunktswinkel
alpha gegeben ist. |
Umkreis
...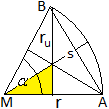 ... ... |
Der Umkreis des Kreisausschnitts ist der Umkreis des
Dreiecks MAB. Der Mittelpunkt des Umkreises ist der Schnittpunkt der Mittelsenkrechten.
Die Mittelsenkrechte des Winkels alpha ist zugleich Winkelhalbierende.
Es gilt cos(alpha/2) = (1/2)r/ru oder
ru
= (1/2)r/cos(alpha/2). |
Inkreis
...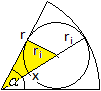 ... ... |
Der Mittelpunkt des Inkreises liegt auf der Winkelhalbierenden
des Mittelpunktswinkels alpha. Fällt man das Lot vom Mittelpunkt auf
einen Radius, so entsteht ein rechtwinkliges Dreieck, und es gilt sin(alpha/2)
= ri/x also x=ri/sin(alpha/2).
Es gilt weiter r = ri+x oder r = ri+ri/sin(alpha/2)
oder ri = r/[1+1/sin(alpha/2)] oder ri = r*sin(alpha/2)/[1+sin(alpha/2)]. |
Zahlenbeispiel
...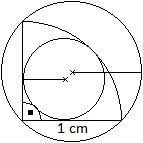 ... ... |
Gegeben: r=1 cm, alpha = 90°. Gesucht:
ru, ri
ru = (1/2)r/cos(alpha/2) = 1/2 cm/ cos(45°)=
(1/2)/[(1/2)sqrt(2)] cm oder (1/2)/sqrt(2) cm oder ungefähr 0,7 cm.
ri = r*sin(alpha/2)[1+sin(alpha/2)]
= sin(45°)/[1+sin(45°)] cm = (1/2)sqrt(2)/[1+(1/2)sqrt(2)]
cm = sqrt(2)-1 cm oder ungefähr 0,4 cm. |
Größtes
Rechteck im Kreisausschnitt top
...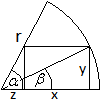 ... ... |
Ein Rechteck mit den Seiten x und y wird in einen Kreisausschnitt
gelegt, wie es die Zeichnung zeigt.
Welches Rechteck hat den größten Flächeninhalt?
Man verbindet den Mittelpunkt mit dem gegenüberliegenden
Eckpunkt und bringt statt der Seiten x und y den Winkel beta ins Spiel. |
Die Zielfunktion ist A(x,y)
= xy.
> Es gilt sin(beta) = y/r oder y = r*sin(beta).
> Es gilt cos(beta) = (z+x)/r oder z+x = r*cos(beta)
oder x = r*cos(beta)-z.
Weiter gilt cot(alpha) = z/y oder z = y*cot(alpha) =
r*sin(beta)cot(alpha).
Dann ist x = r*cos(beta)-z = r*cos(beta)-r*sin(beta)cot(alpha).
Die Zielfunktion ist jetzt
A(beta) = yx = [r*sin(beta)][r*cos(beta)-r*sin(beta)*cot(alpha)]
oder A(beta) = r²[sin(beta)cos(beta)-cot(alpha)sin²(beta)]
oder A(beta) = r²[(1/2)sin(2beta)-cot(alpha)sin²(beta)]
Die Ableitung ist A'(beta) = r²[cos(2beta)-cot(alpha)2sin(beta)cos(beta)]
A'(beta) = r²[cos(2beta)-cot(alpha)sin(2beta)]
A'(beta) = 0 führt zu cos(2beta)-cot(alpha)sin(2beta)
= 0 oder tan(2beta) = tan(alpha) oder beta = alpha/2.
Ergebnis
Die Ecke des größten Rechtecks im Kreisausschnitt
liegt auf der Winkelhalbierenden.
Quellen
https://www.mathelounge.de/78142/extremwertaufgabe-rechteck-in-kreissektor
http://www.onlinemathe.de/forum/Extremwertaufgabe-Rechteck-in-Kreissektor
Größte
Fläche und kleinster Umfang top
Es folgen zwei typische Extremwertaufgaben
mit einer Zielfunktion und einer Nebenbedingung.
Maximaler Flächeninhalt
...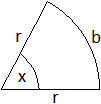 ... ... |
Gegeben ist der Umfang U = 2r+b eines Kreisausschnitts.
Gesucht ist der Mittelpunktswinkel x, bei dem der Flächeninhalt
A = (1/2)r²x maximal ist. |
Lösung
Zielfunktion: A(r,x) = (1/2)r²x, Nebenbedingung:
U = 2r+b oder U = 2r+rx oder rx = U-2r oder x = U/r-2.
Dann ist A(r) = (1/2)r²(U/r-2) = (1/2)Ur-r²
und A'(r) = (1/2)U-2r.
Die Bedingung A'(r) = 0 führt zu r = (1/4)U. Da
A''(r) = -2<0 ist, liegt eine Maximalstelle vor.
Ist r = (1/4)U, so ist x = 2 oder alpha = (180°/pi)x
= 360°/pi oder angenähert alpha = 114,6°.
Ergebnis
Der Flächeninhalt des Kreisausschnitts wird bei
gegebenem Umfang bei einem Winkel von 2 rad = (360/pi)° maximal.
Minimaler
Umfang
...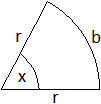 ... ... |
Gegeben ist der Flächeninhalt A = (1/2)r²x
eines Kreisausschnitts.
Gesucht ist der Mittelpunktswinkel, bei dem der Umfang
U= 2r+b minimal ist. |
Lösung
Zielfunktion: U(r,x) = 2r+b oder U = 2r+rx , Nebenbedingung:
A = (1/2)r²x oder x = 2A/r²
Dann ist U(r) = 2r+rx oder U(r) = 2r+2A/r und U'(r) =
2-2A/r².
Die Bedingung U'(r) = 0 führt zu r² = A oder
r = sqrt(A). Da U''(r) = +4A/r³>0 ist, liegt eine Minimalstelle vor.
Ist r = sqrt(A), so sind x = 2 rad, b = 2r und alpha
= (180°/pi)x = 360°/pi oder angenähert alpha = 114,6°.
Ergebnis
Der Umfang des Kreisausschnitts wird bei gegebenem Flächeninhalt
bei einem Winkel von 2 rad = (360/pi)° minimal.
Vergleich
...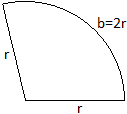 ... ... |
In beiden Fällen gelangt man zu demselben Kreisausschnitt.
Es ist kein Zufall, dass mit einem maximalen Flächeninhalt
ein minimaler Umfang einhergeht.
Überlegungen zu Aufgaben dieser Art stehen auf meiner
Seite Extremwertaufgaben mit Nebenbedingung
unter Paare von Aufgaben. |
Kreisausschnitt
als Kegelmantel top
Zum Kegel
...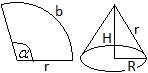 ... ... |
Breitet man den Mantel eines Kegels in der Ebene aus,
so entsteht ein Kreisausschnitt. Umgekehrt kann man aus einem Kreisausschnitt
einen Kegel formen. Werden der Radius r und der Mittelpunktswinkel alpha
vorgegeben, so kann man sich fragen, wie groß die Höhe H und
der Grundkreisradius R des zugehörigen Kegels sind. |
Lösung
Offenbar wird aus dem Radius r des Kreisausschnitts die
Seitenlänge des Kegels und der Kreisbogen b wird zum Umfang des Grundkreises
des Kegels.
Es gilt also b = 2pi*R oder (pi*r)(alpha/180°) =
2pi*R oder R = r(alpha/360°).
Weiter ist H² = r²-R² = r²- [r(alpha/360°)]²
= r²[1-(alpha/360°)²] oder H = r*sqrt[1-(alpha/360°)²].
Ergebnis
Ein Kreisausschnitt mit den Größen r und alpha
führt zu einem Kegel mit dem Radius R= r(alpha/360°) und der Höhe
H = r[1-(alpha/360°)].
Größter
Kegel
Ein bekanntes Extremwert-Problem ist das folgende.
Gegeben ist ein Kreisausschnitt durch den Radius r und
den Mittelpunktswinkel alpha. Wie muss der Winkel gewählt werden,
damit das Volumen des Kegels, den man daraus formen kann, einen Maximalwert
annimmt.
Lösung
...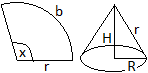 ... ... |
Der Kegel hat des Volumen V = (1/3)pi*R²H.
Es gilt R = r(alpha/360°) oder im Bogenmaß
R = rx/(2pi).
Es gilt H = r[1-(alpha/360°)²] oder mit dem
Bogenmaß H = r*sqrt[1-x²/(2pi)²] =[r/(4pi²)]*[sqrt(4pi²-x²)]. |
Das führt zur Zielfunktion V(x) = (1/3)pi*[rx/(2pi)]²*[r/(4pi²)]*[sqrt(4pi²-x²)]
= ...
oder V(x) = (1/24)(r³/pi²)x²*sqrt(4pi²-x²)
= cx²*sqrt(4pi²-x²) mit c=(1/24)(r³/pi²).
Es ist einfacher, statt nach dem Maximum von V(x) nach
dem des Quadrats V²(x) zu suchen.
Es gilt V²(x) = c²x4(4pi2-x2)
oder V²(x) = c²x4(4pi2-x2) oder
V²(x) = c²(4pi2x4-x6). Dann
ist [V²(x)]' = c²(16pi2x3-6x5).
[V²(x)]' = 0 führt zu 16pi2-6x2=0
oder x² = (8/3)pi² oder x = (2/3)sqrt(6)pi. Auf eine Bestätigung
von [V²(x)]'' < 0 verzichte ich.
Ergebnis
Bei einem Mittelpunktswinkel von x = (2/3)sqrt(6)pi
rad = 2sqrt(6)*60° oder ungefähr 293,9° nimmt der Kegel
das größte Volumen an.
Form
des größten Kegels
Die Form des Kegels wird durch das Verhältnis des
Radius
zur Höhe beschrieben.
...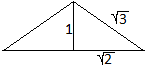 ... ... |
R = (rx)/(2pi) = r[(2/3)sqrt(6)pi]/(2pi) = (1/3)sqrt(6)r
H² = r²-R² = r²-(6/9)r² =(1/3)r²
oder H = (1/3)sqrt(3)r
R:H = [(1/3)sqrt(6)r]:[(1/3)sqrt(3)r] oder R:H = sqrt(2):1 |
Kreisausschnitte
auf meinen Webseiten top
Alle Sehnenvierecke aus vier Kreisausschnitten

Mehr auf meiner Webseite Sehnenviereck
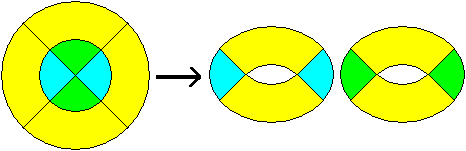
Gleichdick aus Kreisausschnitten
 Mehr auf meiner Webseite Gleichdick
Mehr auf meiner Webseite Gleichdick
Eilinien
Mehr auf meiner Webseite Eilinien.
Verschiedenes
Zum Kreis gehören die
Kreisteile Kreisausschnitt und Kreisabschnitt, zur Kugel gehören die
folgenden Kugelteile.

Mehr auf meiner Webseite Kugelteile
Zum Schluss noch ein paar Zappelbilder
Linse
|
Bogendreieck
|

Vierzack
|
Fünfeck
|
Kreisausschnitt
im Internet top
Deutsch
Heinz Schumann
Medienspezifische
Methodenvielfalt bei der Behandlung einer Extremwertaufgabe
Kai Noack (Mathelounge)
Extremwertaufgabe:
Rechteck in Kreissektor, Kreissektor
2 mit einbeschriebenem Kreis
Wikipedia
Kreissektor,
Kreisbogen,
Kreissegment,
Kreiswinkel,
Kreisdiagramm
Englisch
Eric W.Weisstein (MathWorld)
Circular
Sector, Arc,
Circular
Segment,
Reuleaux
Triangle,
Quarter-Tank
Problem, Circle-Circle
Intersection, Triangle
Arcs,
Quarter-Tank
Problem
Jim Wilson
Maximum
Area of a Sector of a Circle - Fixed Perimeter
Math Open Reference
Sector
area, Area of
a Circle Segment Given the Central Angle, Area
of a Circular Segment given its height
Wikipedia
Circular
sector, Circular
segment, Central
angle, Pie chart
Feedback: Emailadresse auf meiner Hauptseite
URL meiner Homepage:
https://www.mathematische-basteleien.de/
© Dezember 2016 Jürgen
Köller
top |


 ...
... ...
... ..
.. ...
...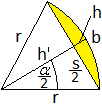 ...
... ...
... ...
... ...
... ...
...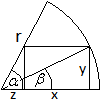 ...
...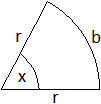 ...
... ...
... ...
... ...
... ...
...