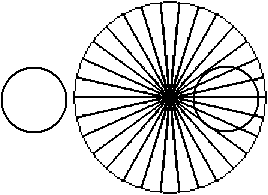
|
Was sind Zweikreisfiguren?
Wie der Name sagt, sind es Figuren aus zwei Kreisen.
Man erhält einen Überblick über diese Figuren,
wenn man einen Kreis festhält und den anderen so lange verschiebt,
bis die Kreise konzentrisch liegen.
Sonderfall r=R
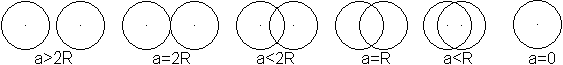
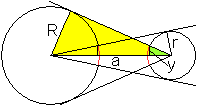
Die Radien R und r der Kreise und die Entfernung a der
Mittelpunkte der Kreise bestimmen eine Figur.
Die Kreise
liegen nebeneinander
top
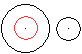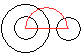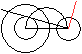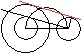
Tangentenproblem
...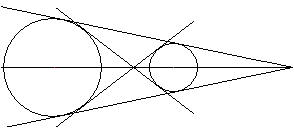 ... ... |
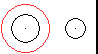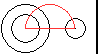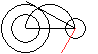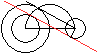
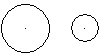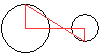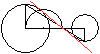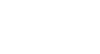
Es ist möglich, an zwei nebeneinander liegende Kreise
je zwei äußere und innere Tangenten zu legen.
Es entsteht eine achsensymmetrische Figur. Von Interesse
ist, in welchen Punkten sich die Tangenten paarweise schneiden und wie
lang die Tangentenabschnitte sind. Tangentenabschnitte sind die Strecken
zwischen den Berührpunkten und den Schnittpunkten. |
Erste
Konstruktion der Tangenten
... ... ... |
Alle Zweikreisfiguren sind achsensymmetrisch.
Die Gerade durch die Mittelpunkte ist die Symmetrieachse.
Zwei Kreise sind ähnlich und können durch eine
zentrische Streckung auseinander hervorgehen. Das Zentrum liegt auf der
Symmetrieachse. Die Verbindungslinie der "Südpole" ist eine Zuordnungsgerade
und kann zur Ermittlung des Zentrums herangezogen werden. |
Die Berührpunkte der gemeinsamen Tangente sind einander
zugeordnet.
Die Berührradien stehen senkrecht auf der Tangente.
Diese Eigenschaften führen
zu den folgenden Konstruktionen der Tangenten.
Der rote Halbkreis ist der Halbkreis des Thales.
Die beiden folgenden Konstruktionen
scheinen die Standard-Konstruktionen zu sein.
Zweite Konstruktion der Tangenten
... ... ...
|
>Zeichne in den großen Kreis einen Kreis mit einem
Radius, der gleich der Differenz der gegebenen Radien ist.
>Zeichne den Halbkreis des Thales über die Verbindungslinie
der Mittelpunkte.
>Verbinde den Schnittpunkt Thaleskreis/Differenzenkreis
und den Mittelpunkt des kleinen Kreises.
>Zeichne die Senkrechte zu dieser Geraden durch den Mittelpunkt
des kleinen Kreises.
>Zeichne zu dieser Geraden die Parallele durch ihren
Schnittpunkt mit der Kreislinie des kleinen Kreises. Das ist die Tangente. |
... ... ... |
>Zeichne um den großen Kreis einen Kreis mit einem
Radius, der gleich der Summe der gegebenen Radien ist.
Beschreibung wie oben. |
Quelle: Zum Beispiel (1) Seite 12f.
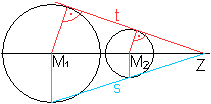
Rechnung
zu den äußeren Tangenten
...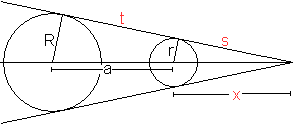 ... ... |
Gegeben seien die Radien R und r der Kreise
und die Entfernung a ihrer Mittelpunkte.
Dann ist x die Entfernung des Schnittpunktes der Tangenten
vom Mittelpunkt des kleineren Kreises. Die Tangentenabschnitte sind s und
s+t.
Es gilt x=(ra)/(R-r), s=r*sqrt[a²-(R-r)²]/(R-r),
t=sqrt[a²-(R-r)²]. |
Zur Herleitung
Die Entfernung x ergibt sich aus dem zweiten Strahlensatz
x:(a+x)=r:R.
Für den Tangentenabschnitt s gilt nach dem Satz
des Pythagoras s²=x²-r².
Für die Entfernung t der Berührpunkte gilt
wieder der zweite Strahlensatz s:(s+t)=r:R.
Rechnung
zu den inneren Tangenten
...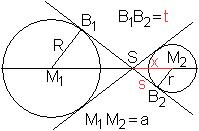 ... ... |
Gegeben seien die Radien R und r der Kreise
und die Entfernung a ihrer Mittelpunkte.
In Analogie zum Fall der äußeren Tangenten
lassen sich die Längen der Strecken x=SM2, s=SB2
und t=B1B2 herleiten.
Es gilt x=(ra)/(R+r), s=r*sqrt[a²-(R+r)²]/(R+r),
t=sqrt[a²-(R+r)²]. |
Eyeball
theorem ("Augapfel-Satz")
...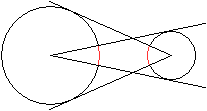 ... ... |
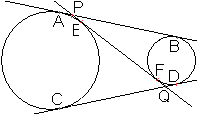
Zeichnet man von den Mittelpunkten zweier nebeneinander
liegender Kreise aus die Tangenten, so entstehen zwei Kreisbögen.
Es gilt der Satz: Die Sehnen zu diesen Kreisbögen
sind gleich lang. |
Beweis
Man ergänzt die Figur und entdeckt ähnliche
Dreiecke, nämlich die gelbgrünen und die grünen.
Es gelten zwei Proportionen.
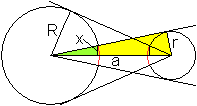
r:a=x:R
|
R:a=y:r
|
Aus den Proportionen folgen die Produktgleichungen Rr=ax
und Rr=ay. Daraus folgt x=y, w.z.b.w..
Zum Namen
...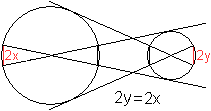 ... ... |
Die beiden Kreise können als Augäpfel mit gleich
großen Bildern gedeutet werden. |
Quelle: Alexander Bogomolny
The
Eyeball Theorem (Mit Applet und Beweis)
Gleiche Tangentenabschnitte
... ... ... |
Zeichnet man zwei äußere und eine innere Tangente,
so entstehen auf der inneren Tangente zwei gleiche Tangentenabschnitte. |
Beweis
Es gilt für die äußeren Tangenten AB=CD
oder AP+PB=CQ+QD.
Die Tangentenabschnitte AP und PB außen sind gleich
den Tangentenabschnitten PE und PF innen.
Die Tangentenabschnitte QD und CQ außen sind gleich
den Tangentenabschnitten QF und QE innen.
Somit kann man die äußeren Tangentenabschnitte
durch die inneren ausdrücken AB=PE+PF und CD=QF+QE.
Mit AB=CD ergibt sich PE+PF=QF+QE.
Da PF=PE+EF und QE=QF+FE gelten, ist PE+EF=QF+FE oder
PE=QF, wzbw.
Quelle: Eckard Specht (Math4U) K.27 (URL
unten).
Riemengetriebe
...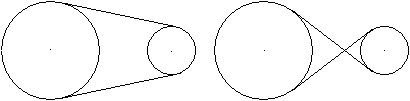 ... ... |
Die beiden Zeichnungen können als Darstellungen
eines Riemengetriebes aufgefasst werden.
Ein kleines Rad z.B. ist mit einem Motor verbunden, das
doppelt so große Rad wird angetrieben. Zwei Beobachtungen:
>Die Räder laufen links gleichsinnig, rechts gegensinnig.
>Das große Rad dreht sich halb so schnell wie das
kleine. |
Schwerpunkt
...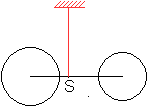 ... ... |
Man kann die beiden Kreise als Scheiben auffassen, die
proportional zu ihren Flächen eine Masse haben und damit im Schwerefeld
der Erde eine Gewichtskraft.
Es gibt zwischen den Mittelpunkten den sogenannten Schwerpunkt.
Verbindet man die Scheiben durch eine gewichtslose Stange und befestigt
im Schwerpunkt eine Schnur, so liegt die Stange horizontal. |
Berechnung der Lage des Schwerpunktes
...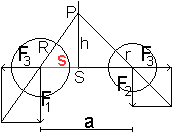 ... ... |
Die beiden Kreise sollen die Radien R und r haben, und
die Entfernung der Mittelpunkte sei a.
Die Gewichtskräfte der Scheiben seien F1
und F2, ihre Massen m1 und m2.
Die Lage des Schwerpunktes wird zum Bespiel durch die
Strecke s festgelegt.
Man führt die fiktiven Kräfte F3
ein, die sich aufheben, die aber zu einer (nicht eingezeichneten) resultierenden
Kraft führen, die vertikal liegt und in P angreift. Der Schwerpunkt
liegt unter P (und auf der Verbindungslinie der Mittelpunkte). |
Es gelten auf Grund ähnlicher Dreiecke die Proportionen
F1:F3=h:s und F2:F3=h:(a-s).
Daraus folgt F1*s=F2*(a-s) oder
F1:F2=(a-s):s oder m1:m2=(a-s):s
oder s=(am2)/(m1+m2).
Im Falle von Kreisscheiben kann man für die Massen
noch setzen: m1:m2=(pi*R²):(pi*r²)=R²:r².
Es gilt damit (a-s):s=R²:r².
Daraus folgt s=(ar²)/(R²+r²).
Sonderfall: Ist r=R, so gilt s=a/2.
Zwillinge
des Archimedes
|
Mehr findet man auf meiner Seite Arbelos. |
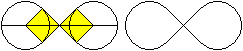
Acht-Kurven
Die Kreise berühren
sich top
Vierteilung des Kreises
... ... ... |
In der Figur links gilt R=2r.
Dann ist die große Fläche A1=4*pi*r²
und die kleine A2=pi*r².
Zeichnet man noch daneben einen zweiten Kreis ein, so
wird der große Kreis in vier gleiche Teile aufgeteilt. |
 |
Verschiebungsproblem
...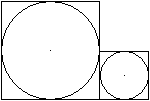 ... ... |
Zwei Quadrate mit ihren Inkreisen liegen wie links dargestellt
nebeneinander.
Man lässt die Quadrate weg und verschiebt den kleinen
Kreis horizontal so weit, dass er den großen Kreis berührt.
Wie groß ist die Verschiebung? |
... ... ... |
Lösung
...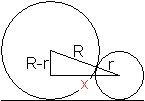 ... ...
|
Liegen die Kreise in den Quadraten, haben ihre Berührpunkte
unten die Entfernung R+r.
Nach dem Verschieben gilt für die neue Entfernung
der Berührpunkte x die Gleichung x²=(R+r)²-(R-r)²
oder x=2*sqrt(rR).
Damit ist die Verschiebung (R+r)-x=R+r-2sqrt(rR). |
Kreis
im Kreisabschnitt
...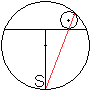 ... ... |
Gegeben sei ein großer Kreis und eine Sehne, die
einen Kreisabschnitt erzeugt.
Die Mittelsenkrechte der Sehne schneidet den großen
Kreis in S.
Im Kreisabschnitt liegt ein beliebiger Kreis, der Kreislinie
und Sehne berührt.
Satz: Zeichnet man eine Gerade durch die Berührpunkte,
so geht die Gerade durch Punkt S. |
Zum Beweis
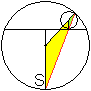 |
Das gelbgrüne und das grüne Dreieck sind ähnlich. |
Quelle:Alexander Bogomolny Inversion
(Mit Applet und Beweis)
Zwei
Kreise im Rechteck
...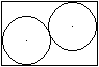 ... ... |
Gegeben sei ein passendes Rechteck. Es sollen zwei gleiche,
möglichst große Kreise in das Rechteck eingepasst werden. |
Lösung
...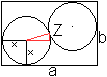 ... ... |
Gegeben sind die Länge a und die Breite b eines
Rechtecks. Gesucht ist der Radius x der Kreise.
Die Figur ist punktsymmetrisch mit dem Zentrum Z(a/2|b/2).
Nach dem Satz des Pythagoras gilt für das rote Dreieck x²+(b/2-x)²=(a/2-x)²
oder x²-(a+b)x+(b²+a²)/4=0. |
Die quadratische Gleichung hat die
Lösung x=(a+b)/2-(1/2)sqrt(2ab). Die andere Lösung führt
zu einem zu großen Radius.
Ist das Rechteck ein Quadrat, so
gilt a=b und x=a-(1/2)[sqrt(2)]a.
Ist das Rechteck (als Grenzfall)
ein Doppelquadrat, so gilt a=2b und x=b/2.
Quelle:
schülerzirkel
mathematik Zwei
Kreise in einem Rechteck Problem des Monats
Juni 2004.
Dort wird ein A4-Blatt untersucht.
Eine
Kollinearität
...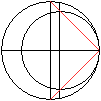 ... ... |
Gegeben seien zwei verschieden große Kreise, wobei
der kleine Kreis den großen innen berührt. Weiter seien die
horizontal liegende Symmetrieachse und zwei zur Achse Senkrechte durch
die Mittelpunkte gegeben.
Verbindet man den gemeinsamen Berührpunkt mit den
Endpunkten des Durchmessers des großen Kreises, so verlaufen diese
Verbindungsgeraden auch durch die Endpunkte des Durchmessers des kleinen
Kreises. |
Zum Beweis
Oben wurde schon angemerkt, dass zwei Kreisen eine zentrische
Streckung zugrunde liegt. Das Zentrum liegt hier im Berührpunkt der
Kreise und die "Nordpole" sind einander zugeordnete Punkte.
Quelle: Science Buddies Tangent
Circles and Triangles
THE
CRESCENT PUZZLE von Dudeney
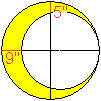
|
Gegeben sind die beiden Strecken zwischen den Kreisen.
Gesucht sind die Radien der Kreise. |
Lösung
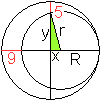 |
Nach dem Satz des Pythagoras gilt r²=x²+y².
Man erhält aus 2R=2r+9 die Angabe x=R-r=4,5.
Man erhält aus R=y+5 die Angabe y=R-5. Dann ist
y=(r+4,5)-5=r-0,5.
Aus der ersten Gleichung folgt r²=(r-0,5)²+4,5².
Das führt zu r=20,5 und R=25, wzbw.. |
Quelle: Dudeney, Henry Ernest, 1857-1930 Amusements in Mathematics
(191.)
Zykloiden
...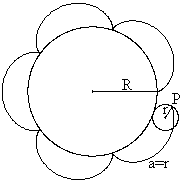 ... ... |
Gegeben ist ein großer Kreis und ein kleiner, der
auf dem großen abrollt. Verfolgt man dabei zum Beispiel einen Punkt
auf der Kreislinie des kleinen Kreises, so entsteht eine Zykloide.
Mehr über Zykloiden findet man auf meiner Seite Spirograph. |
Die Kreise
schneiden sich
top
Kreis als Ortslinie
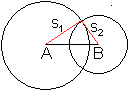
|
Wo liegen die Punkte, die vom Punkt A die Entfernung
s1 und von B die Entfernung s2 haben? |
Tangentenproblem
...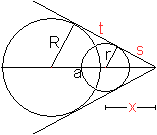 ... ...
|
Von Interesse sind der Schnittpunkt der Tangenten und
die Lage der Berührpunkte.
Es gilt x=(ra)/(R-r), s=r*sqrt[a²-(R-r)²]/(R-r),
t=sqrt[a²-(R-r)²].
Die Herleitung erfolgt wie bei den äußeren
Tangenten nebeneinander liegender Kreise oben. |
Schnittpunkte
der Kreise
...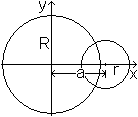 ... ... |
Zur Bestimmung der Schnittpunkte der Kreise legt man
sie am besten passend in ein kartesisches Koordinatensystem.
Die Gleichungen x²+y²=R² und (x-a)²+y²=r²
beschreiben die beiden Kreise. |
Man eliminiert aus beiden Gleichungen y².
Aus R²-x²=r²-(x-a)² ergibt sich die
Abszisse der Schnittpunkte xs=(R²-r²+a²)/(2a).
Aus y²=R²-x² ergeben sich die Ordinaten
ys=[1/(2a)]sqrt[4a²R²-(R²-r²+a²)²]
und ys=-[1/(2a)]sqrt[4a²R²-(R²-r²+a²)²].
Zweikreisfigur (im
engeren Sinne) als Sonderfall
...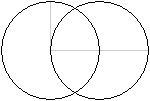 ... ... |
Bei der Zweikreisfigur sind die Radien der beiden Kreise
gleich. Die Mittelpunkte liegen auf der Kreislinie des jeweils anderen
Kreises. Es ist a=r=R.
Dann liefert die Formel oben die Koordinaten der Schnittpunkte
xs= R/2 und ys=(1/2)sqrt(6)R
bzw. ys=-(1/2)sqrt(6)R. |
Die Zweikreisfigur ermöglicht
eine Reihe von Grundkonstruktionen.
...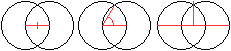 ... ... |
Beispiele sind Halbieren einer Strecke, Zeichnen
eines Winkels von 60° oder Zeichnen einer Senkrechten. |
Quadrat
zwischen den Kreisen
...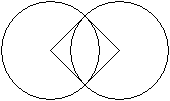 ... ... |
Rücken die Kreise im Vergleich zur Zweikreisfigur
auseinander, so kann es passieren, dass die Mittelpunkte und Schnittpunkte
der Kreise die Ecken eines Quadrates werden.
Es gilt dann a=sqrt(2)*R. |
Längste
Strecke
...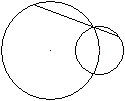 ... ... |
Zeichne durch den Schnittpunkt zweier Kreise eine Gerade.
Es entsteht innerhalb der Kreise eine Strecke, zusammengesetzt aus zwei
Sehnen.
Wie muss die Gerade gelegt werden, damit die Strecke möglichst
lang wird? |
Lösung
... ... ... |
Verbindet man die Endpunkte der Strecke mit dem anderen
Schnittpunkt, so entsteht ein Dreieck. Ganz gleich wie man die Strecke
legt, das Dreieck hat immer die gleichen Winkel. Winkel über demselben
Bogen sind gleich.
Unter den ähnlichen Dreiecken ist das Dreieck mit
dem Durchmesser als Sehne am größten.
So muss die Strecke gelegt werden. |
Quelle: Alexander Bogomolny The
Longest Segment in Intersecting Circles (Mit Applet und Beweis)
Eine
Halbierung
...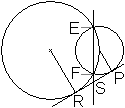 ... ... |
Gegeben seien zwei sich schneidende Kreise und eine gemeinsame
Tangente.
Dann gilt: Die Gerade durch die Schnittpunkte der Kreise
halbiert die Verbindungslinie der Berührpunkte.
Beweis: Es gilt SR²=SF*SE und SP²=SF*SE nach
dem Sekanten-Tangenten-Satz.
Daraus folgt SR=SP. |
Quelle: Mathforum Intersecting
Circles
Orthogonale
Kreise
...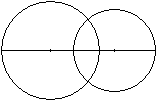 ... ... |
Wie die Zweikreisfigur sind hier auch die beiden verschieden
großen Kreise orthogonal.
Zeichnet man nämlich in den Schnittpunkten Tangenten
an die Kreise, so stehen sie aufeinander senkrecht. |
...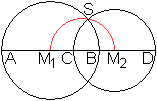 ... ... |
Man findet die beiden Kreise, indem man einen Kreis mit
dem Mittelpunkt M1 vorgibt und einen zweiten (roten) durch den
Mittelpunkt M1 zeichnet. Er schneidet die Achse in M2.
Der orthogonale Kreis ist der Kreis mit dem Mittelpunkt M2,
der durch den Schnittpunkt S der Kreise verläuft. (Der rote Kreis
ist der Halbkreis des Thales.) |
Es gilt der Satz: Sind zwei
Kreise orthogonal, so wird der Durchmesser des einen Kreises durch den
anderen harmonisch geteilt. - In Formeln ausgedrückt heißt das
AC:CB=AD:BD oder AC*BD=CB*AD.
Quelle: (2), Seite 12ff.
Beweis:
Es seien M1M2=a, AM1=R,
M2D=r.
Dann gilt AC=R+(a-r), AD=R+a+r, BD=(a+r)-R, CB=2r-BD=2r-(a+r-R)=r-a+R.
So sind AC*BD=(R+a-r)*(a+r-R)=2rR-R²-r²+a²
und CB*AD=(r+a-R)(R+a+r)=2rR+R²+r²-a².
Da die Kreise orthogonal sind, gilt R²+r²=a².
Das führt zu AC*BD=2rR und CB*AD=2rR.
Daraus folgt AC*BD=CB*AD oder AC:CB=AD:BD,
wzbw.
Da die Rechenschritte umkehrbar
sind, gilt die Umkehrung des Satzes:
Wird der Durchmesser eines Kreises harmonisch durch einen
anderen Kreis geteilt, so sind die beiden Kreise orthogonal.
Parallelenpaar
...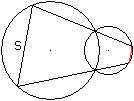 ... ... |
Gegeben seien zwei sich schneidende Kreise und eine Sehne
s. Zeichnet man durch die Endpunkte der Sehne und die Schnittpunkte der
Kreise Geraden, so erzeugen sie im anderen Kreis eine zweite Sehne.
Es gilt der Satz: Die Sehnen sind parallel. |
Zum Beweis
...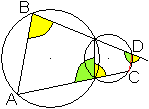 ... ... |
Verbindet man noch die Schnittpunkte der Kreise, so entstehen
zwei nebeneinander liegende Sehnenvierecke. Da gilt der Satz, dass
gegenüberliegende Innenwinkel sich zu 180° ergänzen. Danach
tritt der Winkel bei B auch bei D auf. Nach der Umkehrung des Satzes von
den Stufenwinkeln sind die Sehnen parallel. |
Anmerkung
Es sieht so aus, als seien die beiden Sehnenvierecke
ähnlich, haben sie doch paarweise gleiche Winkel. Aber das ist keine
ausreichende Bedingung. Man denke nur an die Rechtecke.
Trotzdem bleibt das Verhältnis AB/CD konstant, solange
man nur die Lage, aber nicht die Länge der Sehne ändert.
Ergänzung
...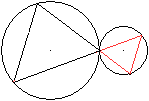 ... ... |
Die Parallelität überträgt sich auch auf
die Figur, bei der sich die beiden Berührpunkte zu einem Punkt zusammenziehen.
Dann entstehen zwei ähnliche Dreiecke in perspektivischer
Lage. |
Quelle: IES (Japan) Circles
"Problem of Two Circles (2)", "Problem of Two Circles(3)"
Die
grasende Ziege
(The grazing goat)
Es handelt sich hier um eine dieser Aufgaben, deren Aufgabenstellung
einfach ist, deren Lösung es aber in sich hat.
...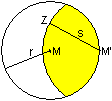 ... ... |
Gegeben sei eine kreisförmige Grasfläche.
Im Randpunkt M' ist ein Pflock eingeschlagen, an dem
ein Seil befestigt ist. An dessen Ende steht die Ziege Z. Wie groß
muss die Länge s des Seils sein, damit die Ziege die Hälfte der
Kreisfläche mit dem Radius r erreichen kann? |
...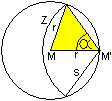 ... ... |
Es ist ungeschickt, die Seillänge
s direkt als Suchvariable einzuführen.
Günstiger ist der eingezeichnete
Winkel x, gemessen im Bogenmaß.
Dann erhält man nach längerer
Rechnung die transzendente Gleichung pi/2 + 2 x * cos(2x) - sin(2x)
= 0 mit der Näherungslösung x = 0,95 rad (=55°).
Das führt näherungsweise
zur Länge des Seils s=1,159r. |
Näheres bei Hans Henschel Puzzles
/ The grazing goat, Solution
Mengendiagramm

1974: Die armen Kleinen.
|
Ein Hinweis auf das Mengendiagramm soll auf dieser Seite
nicht fehlen.
Und was für eine Aufregung gab es um die Mengenlehre
in den 1970er Jahren.
Macht Mengenlehre krank? fragte DER SPIEGEL 1974
in einer Titelgeschichte.
|
Die Kreise
liegen konzentrisch
top
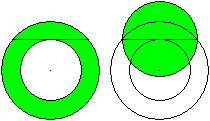
Flächengleicher Kreis
|
Umkreis/Inkreis
|
Aus zwei konzentrischen Kreisen entsteht ein Kreisring.
Mehr darüber findet man auf meiner Seite Ringe. |
Optische Täuschungen
top
Kongruent?
Die beiden Kreise sind kongruent, obwohl
es gar nicht so aussieht.
Gleich
oder verschieden?

Zwei Kreise in zwei Grautönen?
|
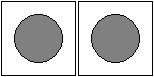
Nein, die Kreise sind identisch. Die Umgebung macht's.
|
Hintereinander

Mit dem Stereoblick sieht man den roten Kreis vor dem
blauen.
|

und hier?
|
Zwei
Stereogramme


Zwei Kreise liegen vor oder hinter einer Ebene.
Zweikreisfiguren
im Internet
top
Deutsch
Eckard Specht (Math4U)
index/ K.1 bis K.76
Florian Modler (matheplanet)
Exkurs:
Potenz eines Kreises
Hans Henschel
Rätsel
/Die grasende Ziege, Lösung
Peter G. Nischke
Zwei
Kreise im Quadrat
Roland Mildner
Zwei
Kreise
Wikipedia
Tangentenviereck,
Kreistangente,
Sekanten-Tangenten-Satz,
Potenz
(Geometrie)
Englisch
Alexander Bogomolny (Cut the Knot)
Inversion,
The
Longest Segment in Intersecting Circles, The
Eyeball Theorem, The
Squinting Eyes Theorem, Tangent
Circles and an Isosceles Triangle, A
Sangaku: Two Unrelated Circles, A
Sangaku Follow-Up on an Archimedes' Lemma, Equilateral
Triangles and Incircles in a Square, In
the Wasan Spirit, Two
Circles in an Angle: What is this about?, Sangaku
Eric W.Weisstein (MathWorld)
Circle-CircleTangents,
Circle-Circle
Intersection, Eyeball
Theorem, Goat
Problem, Venn
Diagram, Monges
CircleTheorem
Sphere-Sphere
Intersection, Double
Bubble
Jeff Kertscher
Tangent
lines to Two Circles
Jim Wilson (Jim Wilson's Home Page)
Comparing
Segments in two circles
Kenneth James Michael MacLean
The
Binary Circle/Sphere Pattern
Nick Hobson (Nick's Mathematical Puzzles)
108.
Eyeball to eyeball
Paul Bourke
Intersection
of two circles
Raymond and Patsy Nasher Collection, Dallas, Texas
Squares with Two Circles (Monolith) "This
is the original"
Wikipedia
Tangent
lines to circles, Power
of a point, Tangential
quadrilateral
Diese Seite enthält
Tipps von Torsten Sillke.
Referenzen top
(1) W.Lietzmann: Altes und neues vom Kreis, Leipzig/Berlin
1935
(2) C.Stanley Ogilvy: Unterhaltsame Geometrie, Braunschweig,
Wiesbaden 1976 [ISBN 3 528 08314 x]
(3) Henry Ernest Dudeney: Amusements in Mathematics (1917)
(Im Internet verfügbar)
Feedback: Emailadresse
auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2007 Jürgen Köller
top |
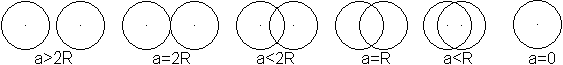
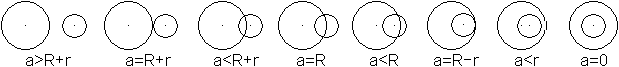
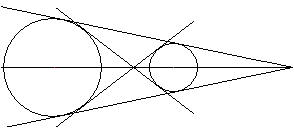 ...
... ...
...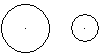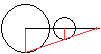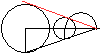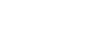
 ...
... ...
... ...
... ...
... ...
...

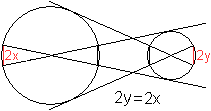 ...
... ...
...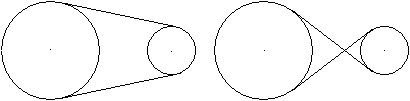 ...
... ...
... ...
...
 ...
...
 ...
... ...
...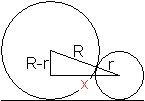 ...
... ...
...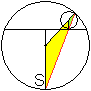
 ...
... ...
... ...
...

 ...
...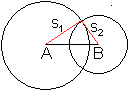
 ...
...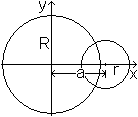 ...
... ...
... ...
... ...
... ...
... ...
... ...
...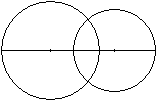 ...
...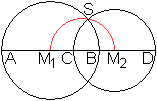 ...
... ...
...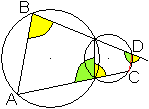 ...
... ...
... ...
... ...
...