|
Was ist der Arbelos?
... ...
|
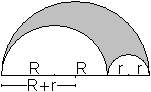
Der Arbelos ist eine sichelförmige Figur, die von
drei Halbkreisen gebildet wird. Die Mittelpunkte liegen auf einer Geraden.
So wie drei Strecken ein Dreieck erzeugen, so erzeugen drei Halbkreise
ein Kreisbogendreieck. Die Radien der unteren Halbkreise seien R und r.
Der Radius des oberen Halbkreises ist dann R+r. |
Der Name Arbelos stammt aus dem Griechischen und bedeutet
Schustermesser, weil die Figur wie das Werkzeug aussieht, das die Schuster
im "alten" Griechenland benutzten [nach (1)].
Größen
des Arbelos top
Umfang
... ...
|
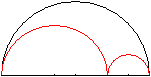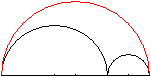
Der Umfang des Arbelos ist U=Pi*(R+r)+Pi*R+Pi*r=2*pi*(R+r).
Das ist auch der Umfang des Kreises mit dem Radius R+r.
Der obere Halbkreisbogen
hat die gleiche Länge wie die beiden unteren Halbkreisbögen
zusammen. |
Inkreis
|
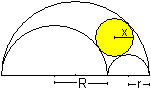
Der Radius des Inkreises ist
|
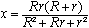
Zur Herleitung der Formel:
... ... |
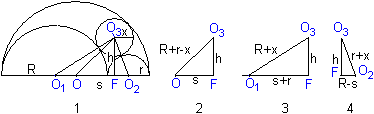(1) Man verbindet die Mittelpunkte und zeichnet das Lot
des Mittelpunktes des Inkreises auf die Horizontale.
Es entstehen drei rechtwinklige Dreiecke, für die
der Satz des Pythagoras gilt. |
Es ergeben sich drei Formeln zur Bestimmung von s, h und
x:
(2) (R+r-x)²=s²+h²
(3) (R+x)²=(s+r)²+h²
(4)(r+x)²=(R-s)²+h²
Das sind drei Gleichungen mit drei Variablen. Nach längerer
Rechnung ergibt sich x=[Rr(R+r)]/[R²+Rr+r²].
Flächeninhalt
Der Flächeninhalt ist A=Pi*(R+r)²/2-Pi*R²/2-Pi*r²/2=Pi*Rr.
Es folgen zwei Deutungen dieser Formel.
... ...
|
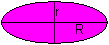
A=Pi*Rr ist der Flächeninhalt einer Ellipse mit
den Halbachsen R und r. |
... ...
|
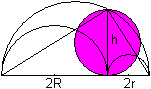Zeichnet man zwischen den beiden kleinen Halbkreisen
eine vertikale Strecke ein, so kann diese als Höhe eines rechtwinkligen
Dreiecks aufgefasst werden.
Nach dem Höhensatz gilt h²=4Rr oder h=2*sqrt(Rr).
Damit ist A=Pi*(h/2)²=Pi*Rr.
Der Flächeninhalt des Kreises mit dem Radius h/2
ist gleich dem Flächeninhalt des Arbelos. |
(Die Größe h/2 ist übrigens das geometrische
Mittel der beiden Radien R und r.)
Der Kreis heißt auch der Kreis des Archimedes.
Mit dem Arbelos ist aufs engste ein rechtwinkliges Dreieck
verbunden. Das Dreieck wird durch die beiden Hypotenusenabschnitte 2R und
2r bestimmt. Das ist ungewöhnlich für die Festlegung eines rechtwinkligen
Dreiecks.
Das Dreieck zum
Arbelos top
Damit ist das grüne Dreieck in Bild 2 unten gemeint.
An der obigen Zeichnung erkennt man schon, dass der Kreis
des Archimedes die kleinen Halbkreise und die Katheten des Dreiecks an
denselben Stellen schneidet. Zum Nachweis verbindet man diese Schnittpunkte
mit dem Fußpunkt der Höhe (rot, 1).
Dann entstehen nach dem Satz des Thales drei rechtwinklige
Dreiecke (2,3). Das grüne Viereck (4) ist ein Rechteck. Der Kreis
des Archimedes ist auch der Umkreis dieses Rechtecks und die Diagonalen
sind zwei Durchmesser.
Die Höhe ist eine Diagonale
des grünen Rechtecks. Die andere schräg liegende Diagonale ist
nicht weniger interessant.
Die Zeichnung zeigt schon, dass der schräg liegende
Durchmesser auch ein Teilstück der gemeinsamen Tangente an die beiden
kleinen Halbkreise ist. Das beweist man so:
(1) Die mit Gelb und Blau markierten Winkel sind nach elementaren
Winkelsätzen gleich groß. Sie ergänzen sich zu 90°.
(2) Zeichnet man die Radien R und r ein, so entstehen
gleichschenklige Dreiecke.
(3,4) Folglich setzen sich die grünen Winkel (4)
aus zwei Winkeln (3) zusammen, die zusammen 90° ergeben. Es liegt eine
Tangente vor, da die Radien Berührradien sind.
Zwillinge des
Archimedes top
Die Höhe des rechtwinkligen
Dreiecks zum Arbelos teilt diesen in zwei Teile. Beide Teilfiguren haben
einen Inkreis. Sie heißen die Zwillingskreise des Archimedes.
|
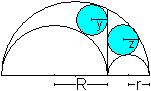
Beide Kreise haben den gleichen Radius und zwar y=z=Rr/(R+r)
oder 2y=2z=2Rr/(R+r)
Die Durchmesser 2y oder 2z sind also das harmonische Mittel
der Radien R und r. |
Zur Herleitung der Formel:
.... .. |
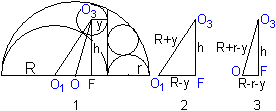Man untersucht zunächst den linken Kreis.
(1) Man verbindet die Mittelpunkte und zeichnet das Lot
des Mittelpunktes des Inkreises auf den Durchmesser.
Es entstehen zwei rechtwinklige Dreiecke, für die
der Satz des Pythagoras gilt. |
Es ergeben sich zwei Formeln zur Bestimmung von y und h:
(2) (R+y)²=h²+(R-y)²
(3) (R+r-y)²=h²+(R-r-y)²
Man eliminiert h und erhält y=Rr/(R+r).
Für h ergibt sich aus (2) h=sqrt(4Ry)=sqrt(4R²r/(R+r)).
... ... |
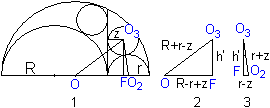Es folgt der rechte Kreis.
(1) Man verbindet die Mittelpunkte und zeichnet das Lot
des Mittelpunktes des Inkreises auf den Durchmesser.
Es entstehen zwei rechtwinklige Dreiecke, für die
der Satz des Pythagoras gilt. |
Es ergeben sich zwei Formeln zur Bestimmung von y und h':
(2) (r+z)²=h'²+(r-z)²
(3) (R+r-z)²=h'²+(R-r+z)²
Man eliminiert h' und erhält wieder z=Rr/(R+r).
Die beiden Zwillingskreise sind also gleich groß.
Für h' ergibt sich aus (2) h'=sqrt(4rz)=sqrt(4Rr²/(R+r)).
Weitere
Aussagen zum Arbelos top
|
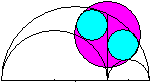
Man kann den Kreis des Archimedes auch um die Zwillingskreise
legen. |
 |
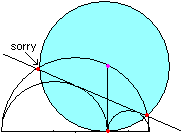Zeichnet man um den oberen Endpunkt der Höhe einen
Kreis mit dem Radius h, so verläuft er auch durch den Schnittpunkt
der gemeinsamen Tangente mit dem großen Halbkreis. |
Das sind nur zwei von vielen Sätzen.
Die Familie
der Zwillinge
top
.... .. |
Oben wurden die Zwillinge des Archimedes behandelt. Es
gibt in der Figur erstaunlicherweise noch viele gleich große Kreise,
die erst vor gar nicht langer Zeit gefunden wurden. |
Die Suche wurde in einem Artikel (2) von "Mathematics Magazine"
unter Federführung von Clayton W.Dodge dokumentiert. Es gibt sage
und schreibe 29 Kreise neben unendlichen Kreisfolgen. Die Bezeichnungen
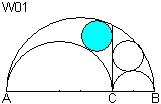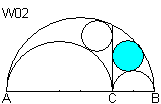
W01, W02, W03, ... gehen auf diesen Artikel zurück. Es folgt eine
Auswahl.
... ... |
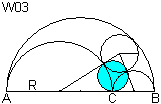Der Kreis W03 ist der Inkreis des Dreiecks, das aus den
Mittelpunkten von drei Kreisen gebildet wird, nämlich dem Inkreis
des Arbelos und den Halbkreisen über AC und CB.
W01, W02 und W03 heißen Bankloffs Tripel. |
... ...
|
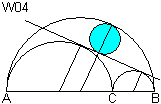
Man zeichnet die gemeinsame Tangente an die Halbkreise
über AC und BC. Es entsteht ein Kreisabschnitt, in den ein größter
Kreis W04 passt.
W01, W02, W03 und W04 heißen Bankloffs Quadrupel. |
... ... |
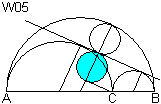Zeichnet man durch den Mittelpunkt des Kreises über
AB eine Senkrechte zur gemeinsamen Tangente, so liegt auf dieser Geraden
der Mittelpunkt eines Zwillingskreises W05, der den Kreis W04 berührt.
W05 ist ein Dodge-Kreis. |
... ...
|
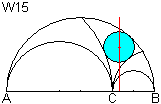
Man zeichnet um den Punkt A einen Kreis mit dem Radius
AC und um Punkt B mit dem Radius BC. Man zeichnet einen Kreis W15, der
diese beiden Kreise berührt.
Zusätzlich berührt er auch den Halbkreis über
AB.
W15 ist ein Schoch-Kreis. |
Die (rote) vertikale Gerade durch den Mittelpunkt des Kreises
W15 heißt Schoch-Gerade. Sie wird bei den beiden nächsten Kreisen
verwendet.
... ...
|
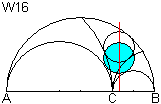
Man zeichnet einen Kreis W16, der die beiden Halbkreise
über AC und CB berührt und dessen Mittelpunkt auf der Schoch-Geraden
liegt.
W16 ist ein Schoch-Kreis. |
... ...
|
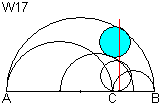
Man gibt einen Halbkreis vor, der über den beiden
Mittelpunkten von AC und CB liegt. Man zeichnet dann einen Kreis W17, der
diesen Halbkreis berührt und durch den Schnittpunkt der Schoch-Geraden
mit dem Halbkreis über AB geht.
W17 ist ein Schoch-Kreis. |
... ... |
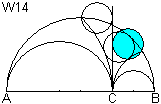Man zeichnet um Punkt B einen Kreis mit dem Radius BC.
Weiter zeichnet man durch den Schnittpunkt dieses Kreises um B mit dem
Kreis über AB einen Kreis W14, der die Vertikale durch C berührt.
W14 ist ein Schoch-Kreis. |
... ...
|
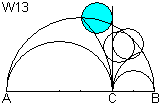Man zeichnet um den Punkt A einen Kreis mit dem Radius
AC. Weiter zeichnet man durch den Schnittpunkt dieses Kreises um A mit
dem Kreis über AB einen Kreis W13, der die Vertikale durch C berührt.
W05 ist ein Schoch-Kreis. |
... ...
|
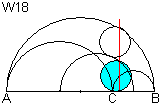
Man gibt einen Halbkreis vor, der über den beiden
Mittelpunkten von AC und CB liegt. Man zeichnet dann einen Kreis durch
den Fußpunkt der Höhe, dem Schnittpunkt der Schoch-Geraden mit
dem oben beschriebenen Halbkreis und durch Punkt C. W18 ist ein Schoch-Kreis. |
... ... |
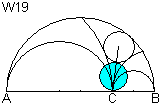Man zeichnet eine Gerade durch den Mittelpunkt des Kreises
W15 und den Berührpunkt C. Dann zeichnet man einen Kreis W19, dessen
Mittelpunkt auf dieser Verbindungslinie liegt und der durch Punkt C verläuft.
W19 ist ein Schoch-Kreis. |
Es fällt auf, dass die
meisten Kreise, die ich hier vorstelle, nach Thomas Schoch benannt sind.
Martin Gardner schrieb 1979 über Bankhoffs Tripel. Das inspirierte
den damaligen Studenten Thomas Schoch aus Essen, weitere Kreise zu entdecken.
Er schickte seine Ergebnisse Gardner, der sie weitergab, weil er nicht
Deutsch verstand. Erst 1996 erhielt Clayton W. Dodge eine Kopie dieser
Arbeit. Er erkannte die Qualität und fand einige Kreise wieder, die
er unabhängig von Schoch entdeckt hatte. Er benannte die Kreise nach
dem ersten Entdecker Schoch.
Pappus-Kette top
Wer die Rechnungen, die ich oben angedeutet habe, wirklich
durchgeführt, merkt, dass sie zum Teil sehr aufwendig sind. Peter
Woo schrieb auf einer Webseite, dass die Beweise der Sätze, die er
aufführt, sechs handgeschriebene Seiten füllen, während
es bei Anwendung der
Kreisinversion bei zwei Seiten bleibt.
Die Kreisinversion soll auf die Pappus-Kette angewandt
werden.
... ... |
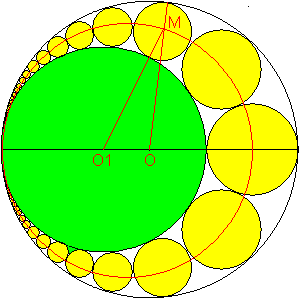Man erhält die Pappus-Kette, wenn man den Arbelos
an der Grundlinie spiegelt und nicht nur einen Inkreis einzeichnet, sondern
anschließend beliebig viele.
Ein Kreis der Kette wird mit dem Mittelpunkt M gekennzeichnet.
Er habe den Radius k. Dann gilt (O1)M+OM=(R+k)+[(R+r)-k]=2R+r. Für
M gilt also, dass die Summe der Abstände von den festen Punkten O1
und O konstant ist. Damit liegt M auf einer Ellipse. Da die Rechnung für
jeden Mittelpunkt eines Kreises der Kette gilt, liegen alle Mittelpunkte
auf einer Ellipse. O1 und O sind die Brennpunkte.
(Die Zeichnung entstand nach einer Vorlage von Dick Klingens,
URL unten.) |
... ... |
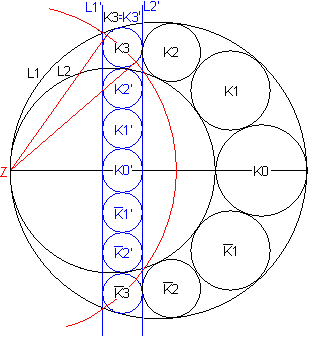Man bekommt nun eine andere Sicht der Kreise der Kette,
wenn man sie am roten Kreis spiegelt. Dazu legt man links das Zentrum Z
fest. Der Kreis wird zum Beispiel so gelegt, dass der Kreis K3 in sich
selbst übergeht.
Dann gehen die Kreise L1 und L2, die zum Teil den Arbelos
bilden, in zwei Parallelen über, da das Zentrum ins "Unendliche" rückt
und eine Beziehung wie Sich-Berühren erhalten bleibt.
Aus der Pappus-Kette wird eine einfache Kreisfolge zwischen
zwei Parallelen.
Man kann der Abbildung entnehmen, dass die Pappuskette
aus beliebig vielen Kreisen bestehen muss. |
Dann kann man noch eine Formel an der Zeichnung ablesen:
Ist r3 der Radius des dritten Kreises K3 der Kette, so
liegt sein Mittelpunkt M3 in einem Abstand von h3=6*r3 von der horizontal
liegenden Symmetrieachse entfernt. Das kann man verallgemeinern zu h(n)=2*n*r(n).
Arbelos im Internet
top
Deutsch
Arndt Brünner
Der
Arbelos — oder die Sicheln des Archimedes: interaktive Graphik
Wikipedia
Arbelos,
Zwillingskreise,
Leon
Bankoff
Englisch
Alexander Bogomolny
The
Shoemaker's Knife
Behnaz Rouhani
The
Arbelos
Bob's Pages
Pappus's
Arbelos
Eric W. Weisstein (World of Mathematics)
Arbelos,
Archimedes'
Circles, Bankoff
Circle, Inversion,
Pappus
Chain,
Schoch
Line,
Woo Circle
Floor van Lamoen
Online
catalogue of Archimedean circles
Harold P. Boas
Reflections
on the Arbelos
Peter Woo
The
ARBELOS
Shannon Umberger
Essay
# 4 - The Arbelos and the Salinon
Stephen Tan
Arbelos
by Steve
Thomas Schoch
The
Arbelos,
My
Arbelos story,
A
Dozen More Arbelos Twins
Wikipedia
Arbelos
Wilson Stothers
The
Arbelos with CabriJava
Holländisch
Dick Klingens
Een,
volgens Pappos, oud probleem: de arbelos
Referenzen top
(1) Martin Gardner: Fractal Music, Hypercards and More
Math. Recreations from SA Magazin, Freeman (1991) New York
(2) Clayton W. Dodge, Thomas Schoch, Peter Y. Woo, Paul
Yiu: Those Ubiquitous Archimedean Circles, Mathematics Magazine, Vol.72,
NO.3, June 1999
(3) C.Stanley Ogilvy: Unterhaltsame Geometrie, Braunschweig
1976 (ISBN 3 528 08314 X)
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2003 Jürgen Köller
top |
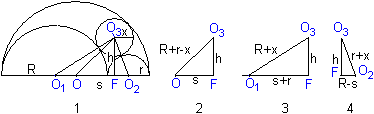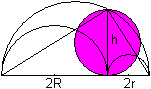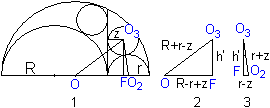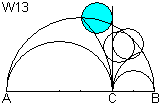