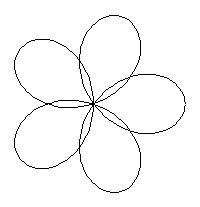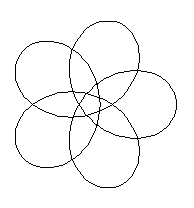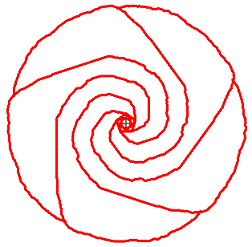
Fünfstrahlige Figuren

Inhalt dieser Seite

Was ist eine fünfstrahlige Figur?
Beispiele fünfstrahliger Figuren
Beispiele fünfstrahliger Körper

Zykloiden
Vermischtes
Fünfstrahlige Figuren im Internet.

Zur Hauptseite "Mathematische Basteleien"

Was ist eine fünfstrahlige Figur?

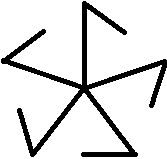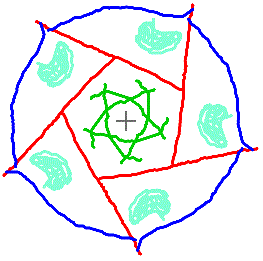
...... Eine fünfstrahlige Figur ist eine drehsymmetrische oder kreissymmetrische Figur von der Ordnung fünf.
Das heißt, dass sie ein Drehzentrum hat und dass sie bei jeder Fünfteldrehung um dieses Zentrum in sich selbst übergeht.
Sie heißt auch fünfzählige Figur. ......

...

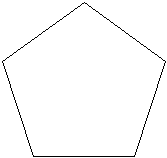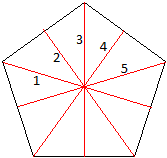
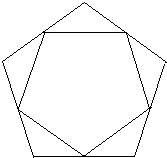
Auch das Fünfeck ist fünfstrahlig.

Bei ihm kommen noch Achsensymmetrien mit fünf Achsen hinzu.

...

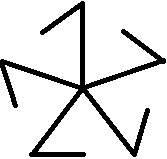...	Zu jeder fünfstrahligen Figur gibt es ein Spiegelbild.

Diese Seite hat den gleichen Aufbau wie meine Seiten
Dreistrahlige Figuren, Vierstrahlige Figuren, Sechsstrahlige Figuren, Siebenstrahlige Figuren , Achtstrahlige Figuren.

Beispiele fünfstrahliger Figuren top
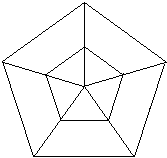
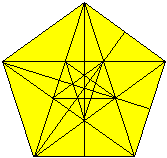
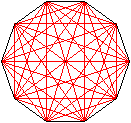
Linien im Fünfeck

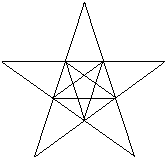
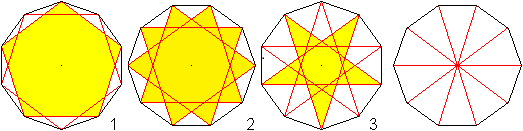
Sterne im Fünfeck

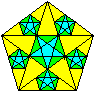
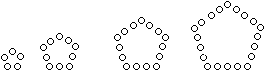
Abkömmlinge der 6-Fünfecke-Figur

Figuren von meinen Webseiten

Zehnstrahlige Figuren sind auch fünfstrahlig.

Zehneck

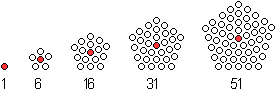
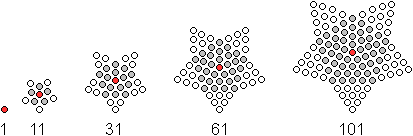
Figurierte Zahlen

Beispiele fünfstrahliger Körper top
Zur Definition

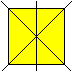
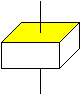
Verschiebt man eine Figur in Normalrichtung, so entsteht ein Prisma.
Ist die Figur vierstrahlig wie hier das gelbe Quadrat, so ist auch das Prisma vierstrahlig.
Dabei wird der Drehpunkt durch eine Drehachse ersetzt.

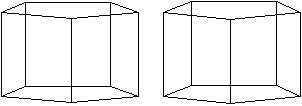
Fünfseitiges regelmäßiges Prisma

....

Ersetzt man das Quadrat durch ein regelmäßiges Fünfeck, entsteht ein fünfseitiges, regelmäßiges Prisma. Die Gerade durch die Mittelpunkte der Fünfecke ist die Drehachse.

Die Bildpaare ermöglichen ein 3D-Bild.

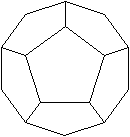
Pentagondodekaeder

...

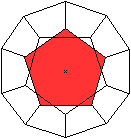Schaut man auf ein Fünfeck, so stellt sich das Dodekaeder als eine fünfstrahlige oder fünfzählige, drehsymmetrische Figur dar.

Die Drehachse ist in der Zeichnung nur ein Punkt.

...

...

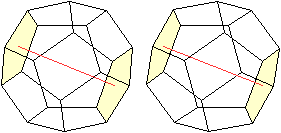Da es sechs Paare von Fünfecken gibt, gibt es auch sechs Drehachsen. Sie verlaufen durch die Mittelpunkte der Fünfecke.

Links ein Beispiel

Ikosaeder

...

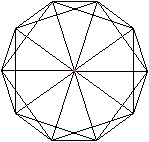Schaut man auf eine Ecke des Ikosaeders, so stellt es sich als eine fünfstrahlige, drehsymmetrische Figur dar. Diese Symmetrie überträgt sich auf das Ikosaeder.

Die Drehachse zeigt sich in der Zeichnung als Punkt in der Mitte.

...

...

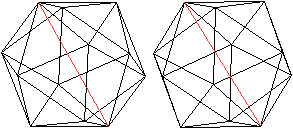Es gibt 12 Eckpunkte und damit 6 Paare von gegenüberliegenden Eckpunkten. Durch sie verlaufen die Drehachsen. Es sind also die längeren Raumdiagonalen.

Links ein Beispiel

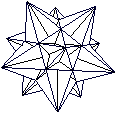
Kepler-Poinsot-Körper
"All four (Kepler-Poinsot Polyhedra) have the same symmetry axes and symmetry planes as the icosahedron and dodecahedron."
Quelle: http://www.georgehart.com/virtual-polyhedra/kepler-poinsot-info.html

Kleines Sterndodekaeder

Großes Sterndodekaeder

Großes Dodekaeder

Großes Ikosaeder

Weitere drehsymmetrische Körper der Ordnung 5

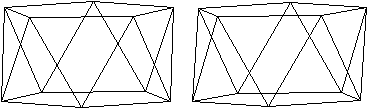
Antiprisma

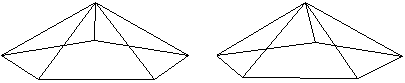
Johnsonkörper J2, Fünfeckpyramide

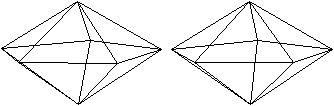
J13 Pentagonale Bipyramide

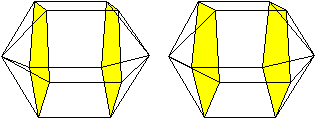
J16 Verlängerte pentagonale Bipyramide

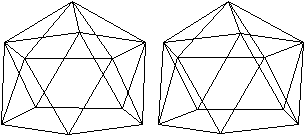J11 Verdreht verlängerte Fünfeckpyramide

Zykloiden top
Eine Herausforderung liegt darin, fünfstrahlige Figuren mit Hilfe von Formeln zu zeichnen. Da bieten sich die Zykloiden an.
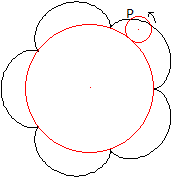
Epizykloide

...... Rollt man den kleinen Kreis außen auf dem großen ab, so beschreibt ein Punkt auf der Kreislinie eine Kurve, die Epizykloide.

.
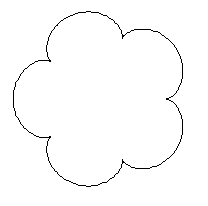x=6cos(t/5)-cos(6t/5)
y=6sin(t/5)-sin(6t/5)

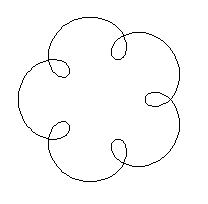
x=6cos(t/5)-2cos(6t/5)
y=6sin(t/5)-2sin(6t/5)

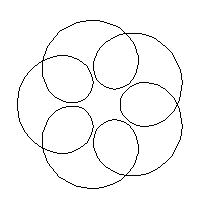
x=6cos(t/5)-4cos(6t/5)
y=6sin(t/5)-4sin(6t/5)

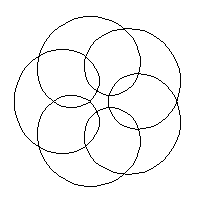
x=6cos(t/5)-5cos(6t/5)
y=6sin(t/5)-5sin(6t/5)

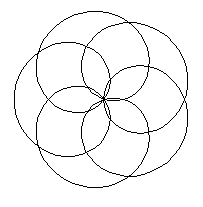
x=6cos(t/5)-6cos(6t/5)
y=6sin(t/5)-6sin(6t/5)

0<=t<=10pi

Hypozykloide

...

...

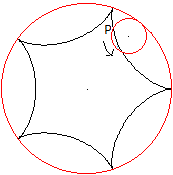
Rollt man den kleinen Kreis innen im großen Kreis ab, so entsteht eine Kurve mit fünf Spitzen, die Hypozykloide.

x=4cos(t/5)+cos(4t/5)
y=4sin(t/5)-sin(4t/5)

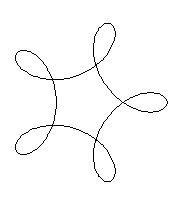
x=4cos(t/5)+2cos(4t/5)
y=4sin(t/5)-2sin(4t/5)

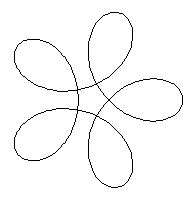
x=4cos(t/5)+3cos(4t/5)
y=4sin(t/5)-3sin(4t/5)

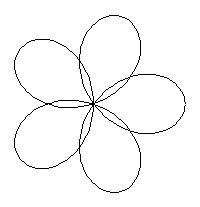
x=4cos(t/5)+4cos(4t/5)
y=4sin(t/5)-4sin(4t/5)

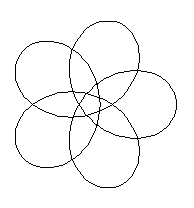
x=4cos(t/5)+5cos(4t/5)
y=4sin(t/5)-5sin(4t/5)

0<=t<=10pi

Polarkurven

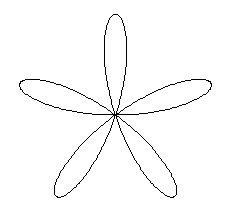
r=sin(5t)

r=sin(5t)^2+2sin(5t)+2

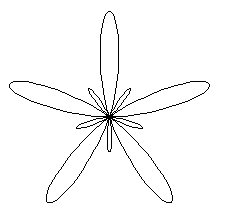
r=sin(5t)-2sin(5t)^2

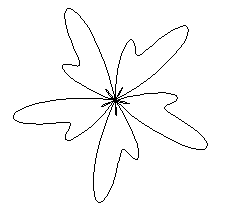
r=3sin(5t)^2-2sin(5t)+1

Vermischtes top
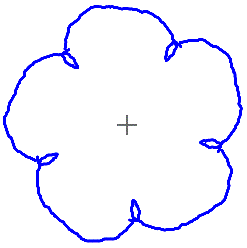
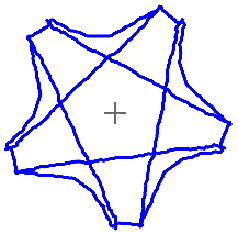
Fünfstrahlige Figuren mit einem Zeichenprogramm
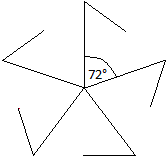
Es gibt im Internet Applets mit dem Namen Kaleidoskop. Sie simulieren jedoch nur den Winkelspiegel. Doch auch diese Bilder sind ansehnlich. Eine fünfstrahlige Figur z.B. entsteht so, dass man nur die Linien in einem Kreisausschnitt mit einem Winkel von 360°/5 =72° zeichnet. Das Programm zeichnet sie gleichzeitig in die übrigen vier Kreisausschnitte ein. Ich weise nur auf das Programm von mathisfun (URL unten) hin.