|
Was sind Polyabolos?
Man kann gleichschenklig-rechtwinklige Dreiecke so aneinander
legen, dass sich mindestens zwei Seiten berühren. Entweder berühren
sie sich zwei Hypotenusen oder zwei Katheten.
Figuren dieser Art heißen Polyabolos, Polytans oder
Supertangrams.
Der Name Polyabolo stammt vom Diabolo her, das im Schnitt
aus zwei Dreiecken besteht. Nach (1) geht dieser Name auf S.J.Collins aus
Bristol zurück und wird von H.O.O'Beirne (New Scientist, 1961) verwendet.
Die Polyabolos unterscheidet man nach der Anzahl der Dreiecke.
Es gibt Diabolos, Triabolos, Tetrabolos, Pentabolos,...
Diabolos und Triabolos
top
... ... ...
|
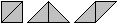
Es gibt drei Diabolos.
Das sind ein Quadrat, ein gleichschenklig-rechtwinkliges
Dreieck und ein Parallelogramm. |
... ... ...
|
Eigentlich paradox: Das Bild des Spielgerätes Diabolo,
des Namensgebers, gehört nicht zu diesen Diabolos. |
|
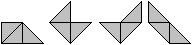
Es gibt vier nur Triabolos. |
Trotzdem kann man aus ihnen ansehnliche Figuren bilden.

|
1, 2 Vergößerte Triabolos
|
3, 4, 5 Konvexe Figuren
|
6 Wegweiser
|
7 Krone
|
8 Liegende Katze
|
Bau der Tetrabolos
top
Es gibt 14 Tetrabolos. Die Anzahl 14 ist eine gute Zahl,
nicht zu groß und nicht zu klein.
...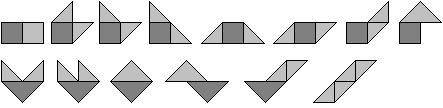 ... ... |
Will man die Figuren finden, sollte man systematisch
vorgehen. Eine Möglichkeit ist, zuerst ein Quadrat aus zwei Dreiecken
vorzugeben und dann in allen Variationen zwei Dreiecke anzulegen. Weiter
gibt man ein Doppeldreieck vor und addiert zwei Dreiecke. Ein Außenseiter
(unten rechts) kommt noch dazu. |
Will man die Tetrabolos als Puzzle-Steine benutzen, sollte
man sie selbst herstellen.
... ... ... |
Man drucke dazu ein Muster aus Quadraten aus, markiere
die 14 Figuren in gewünschter Größe, klebe sie auf Pappe
und schneide sie aus. |
Eigenschaften
der Tetrabolos
top
...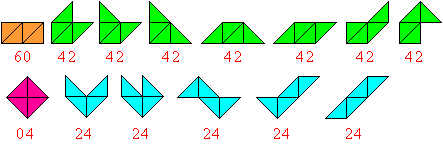 ... ... |
Bei den Tetrabolos sind die Ränder interessant.
Sie werden entweder von einer Quadratseite (Kathete) oder von der Diagonalen
eines Quadrats (Hypotenuse) gebildet.
Zählt man sie aus, unterscheidet man die Klassen
60,
04, 42 und 24.
Die erste Ziffer ist die Anzahl der Katheten, die zweite die Anzahl der
Hypotenusen. |
... |
9 der Tetrabolos sind symmetrisch. |
Rechtecke
mit allen Tetrabolos? top
Man kann in Analogie zu den Pentominos
oder den
Polyiamonds viele Lege-Probleme mit Tetrabolos
untersuchen.
Das Grundproblem besteht wieder darin, Rechtecke aus
allen Tetrabolos zu legen. Es gibt 14 Tetrabolos mit 4*14=56 Halbquadraten
oder 28 Quadraten.
...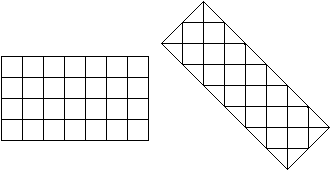 ... ... |
Das sind zwei mögliche Rechtecke.
Das ist erstaunlich: Sie können nicht mit allen Tetrabolos
gelegt werden. |
Ein Möglichkeit, um das nachzuweisen, besteht darin,
die Steine und auch die Figur nach Schachbrettart zu färben und dann
zu vergleichen.
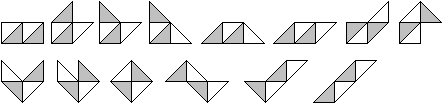 Das hilft z.B. bei Hexominos weiter, hier aber nicht. Es
gibt keine Auffälligkeiten. Alle Steine haben zwei dunkle und zwei
weiße Dreiecke.
Das hilft z.B. bei Hexominos weiter, hier aber nicht. Es
gibt keine Auffälligkeiten. Alle Steine haben zwei dunkle und zwei
weiße Dreiecke.
Man kommt zum Ziel, wenn man nur
die schräg liegenden Hypotenusen, die zum Rand beitragen, auszählt,
und zwar getrennt nach der Richtung.
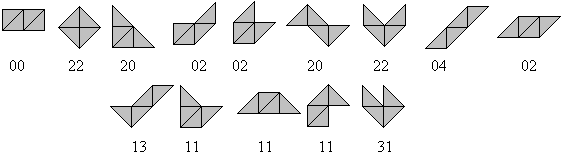 Die erste Zahl bezieht sich auf die Hauptdiagonalenrichtung
(/), die zweite auf die Richtung der Nebendiagonalen (\). Dreht man die
Steine um, so vertauscht sich nur die Reihenfolge der beiden Ziffern der
"Kennzahl". Es bleibt bei der Einteilung der Tetrabolos in Steine mit gerader
und ungerader Anzahl der Hypotenusen einer Richtung. Von der letzten Sorte
gibt es fünf (!) Steine. Damit haben alle Steine zusammen eine ungerade
Anzahl von Hypotenusen einer Richtung außen.
Die erste Zahl bezieht sich auf die Hauptdiagonalenrichtung
(/), die zweite auf die Richtung der Nebendiagonalen (\). Dreht man die
Steine um, so vertauscht sich nur die Reihenfolge der beiden Ziffern der
"Kennzahl". Es bleibt bei der Einteilung der Tetrabolos in Steine mit gerader
und ungerader Anzahl der Hypotenusen einer Richtung. Von der letzten Sorte
gibt es fünf (!) Steine. Damit haben alle Steine zusammen eine ungerade
Anzahl von Hypotenusen einer Richtung außen.
Zurück zu den Rechtecken!
Das 7x4-Rechteck hat alle Hypotenusen innen. Sie bilden
Paare und die Anzahl ist gerade. Andererseits ist für die Steine die
Anzahl der Hypotenusen einer Richtung ungerade. Das ist ein Widerspruch.
Das schräg liegende Rechteck hat außen 16 Hypotenusen
einer Richtung. Das ist eine gerade Zahl. Dieses Rechteck ist deshalb ebenfalls
nicht möglich.
Diese Überlegungen stammen aus Buch (1) und wurde
von O'Beirne entwickelt und 1962 in "New Scientist" veröffentlicht.
Figuren
mit allen Tetrabolos
top
... ... ... |
Will man Figuren aus allen 14 Tetrabolos
entwerfen, muss man also darauf achten, dass die Anzahl der Hypotenusen
einer Richtung, die zum Rand beitragen, ungerade ist. Damit fallen viele
symmetrische Figuren weg, da dann Hypotenusen im allgemeinen paarweise
auftreten.
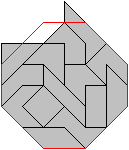
Das symmetrische, rot umrandete
Achteck hat die Kennzahl 44, ist also nicht lösbar. Die abgeänderte
Figur hat die Kennzahl 35. |
Andererseits sind natürlich nicht
alle Figuren mit ungerader Hypotenusenzahl lösbar.
... ... ...
|
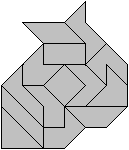
Mit etwas Fantasie erkennt man links einen Tigerkopf.
Die Figur hat die Kennzahl 53. |
Ringe aus Tetrabolos
top
...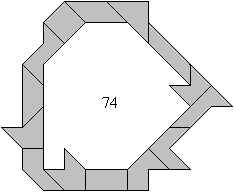 ... ... |
Man kann mit den 14 Tetrabolos einen Ring bauen. Ziel
soll es sein, möglichst viele Dreiecke zu umschließen.
Sind 74 umschlossene gleichschenklig-rechtwinklige Dreiecke
zu überbieten? |
Es gibt eine Vielzahl von Problemen
mit einer Teilmenge der Tetrabolos.
Vergrößerungsproblem
top
...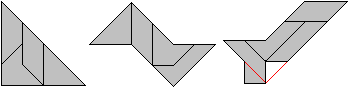 ... ... |
Man kann mit 4 der 14 Tetrabolos die meisten Steine in
doppelter Größe bauen. |
...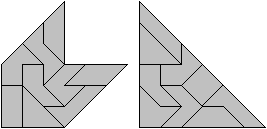 ... ... |
Man kann mit 9 der 14 Tetrabolos einen Stein in dreifacher
Größe bauen. |
Rechtecke
top
Oben wurde gezeigt, dass man keine
Rechtecke mit allen Steinen bauen kann. Aber es ist möglich mit weniger
als 14 Steinen Rechtecke zu finden. Lösungen werden in Buch (1) dargestellt.
Ergebnisse:
Lösbare Rechtecke mit Katheten
als Einheiten: 2x2, 2x3, 2x4, 2x5, 2x6, 3x3, 3x4
Unlösbar: 2x7, 2x8,2x9, 2x10,
2x11, 2x12, 2x13, 2x14, 4x7
Lösbare Rechtecke mit Hypotenusen
als Einheiten: 2x3, 2x4, 2x5, 3x4, 3x6, 3x8, 4x5, 4x6
Unlösbar: 2x7
Weitere Polyabolos
top
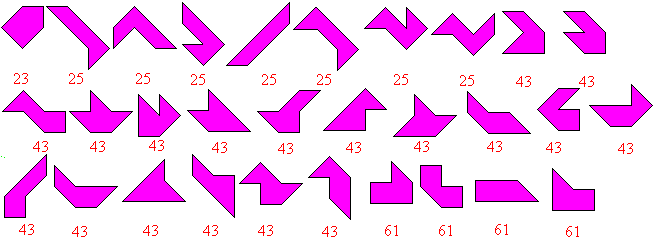
Es gibt 30 Pentabolos, also Polyabolos
aus fünf Steinen. Sie sind hier in vier Klassen eingeteilt.
Wie oben gibt die erste
Ziffer die Anzahl der Katheten im Rand an, die zweite die Anzahl der Hypotenusen.
 Weiter existieren107 Hexabolos, 318 Septabolos, 1106 Oktobolos,
....
Weiter existieren107 Hexabolos, 318 Septabolos, 1106 Oktobolos,
....
Polyabolos im
Internet top
Englisch
Andrew Clarke
Polyaboloes
Eric W. Weisstein
Polyabolo,
Tetrabolo,
Triabolo
Henri Picciotto
Geometric
Puzzles in the Classroom (Tetrabolos=SuperTangrams, got names)
Michael Keller
Counting
Polyforms
Peter F.Esser
Polyaboloes
Wen-Shan Kao (from TAIWAN)
Polytans
(Polyaboloes)
and more
Wikipedia
Polyabolo
Referenzen
top
(1) Martin Gardner: Mathematische Hexereien, Ullstein,
Berlin/Frankfurt/Wien, 1988 (ISBN 3 550065787)
(2) bild der wissenschaft 8/1979, (Halbquadrat-Mehrlinge),
Seite 102ff.
(3) Karl-Heinz Koch: ...lege Spiele, DuMont, Köln
1987 (ISBN 3-7701-2097-3)
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2003 Jürgen Köller
top |




 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
...