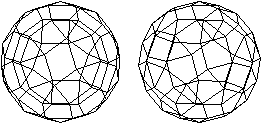|
Was ist das Triakistetraeder?
...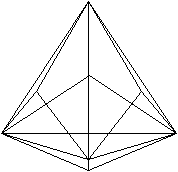 ... ... |
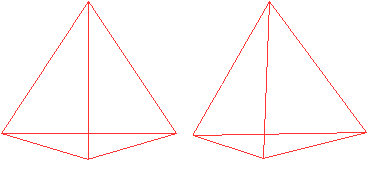
Das Triakistetraeder ist ein mathematischer Körper,
der von 12 gleichschenkligen, kongruenten Dreiecken gebildet wird. Es hat
8 Eckpunkte und 18 Kanten.
An vier Eckpunkten treffen drei, an den anderen vier Eckpunkten
sechs Kanten aufeinander. |
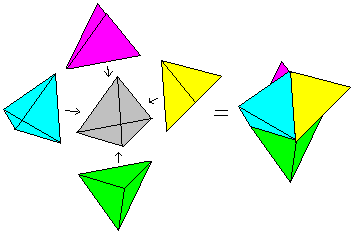
Es entsteht aus einem abgestumpften
Tetraeder, indem man die Mittelpunkte benachbarter Seitenflächen
miteinander verbindet und dann den Körper aus diesen Strecken betrachtet.
Das Triakistetraeder ist der duale Körper des Tetraederstumpfes. Die
Körper, die auf diese Weise aus einem archimedischen Körper entstehen,
heißen Catalan-Körper.
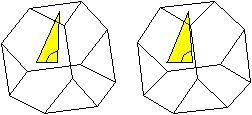
Mit dem Stereoblick sieht
man das Triakistetraeder dreidimensional.
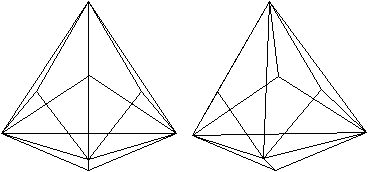
durchsichtig
|
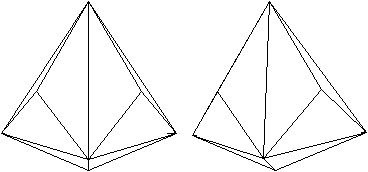
undurchsichtig
|
Erste Annäherung
top
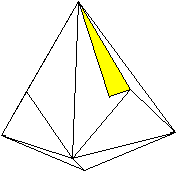
Der Name erklärt sich dadurch, dass das Triakistetraeder
auch entsteht, indem man auf die Seitenflächen eines Tetraeders vier
passende Dreieckspyramiden setzt (tri=drei, acis=spitz).
Man zählt:
>Das Tetraeder hat 4 Seitenflächen. Dann hat das
Triakistetraeder 4*3=12 Seitenflächen.
>Das Tetraeder hat 4 Eckpunkte. Dann hat das Triakistetraeder
4+8=8 Eckpunkte.
>Das Tetraeder hat 6 Kanten. Dann hat das Triakistetraeder
6+4*3=18 Kanten.
Zweite Annäherung
top
...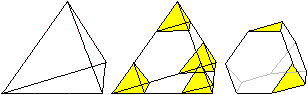 ... ... |
Vorweg: Der Tetraederstumpf entsteht aus einem Tetraeder,
indem man an den Ecken passend dreiseitige Pyramiden abschneidet.
Dazu teilt man die Kanten in drei gleiche Teile. |
Wie oben erwähnt, entsteht
das Triakistetraeder aus dem abgestumpften Tetraeder.
Es werden also die Mittelpunkte benachbarter Seitenflächen
des Tetraederstumpfes miteinander verbunden. Das geschieht in "Handarbeit"
in mehreren Schritten.
... ... ... |
Das abgestumpfte Tetraeder wird von 4 gleichseitigen
Dreiecken und 4 regelmäßigen Sechsecken gebildet. |
...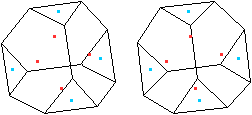 ... ... |
Markiere die Mittelpunkte der 4 Sechsecke in Rot und
zur Unterscheidung die Mittelpunkte der 4 Dreiecke in Blau. |
... ... ... |
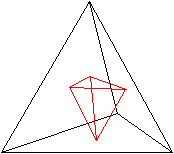
Verbinde die blauen Mittelpunkte der Dreiecke.
Es entsteht das rot markierte "erzeugende" Tetraeder,
auf die noch die vier Dreieckspyramiden gesetzt werden müssen.
Das erfolgt in zwei Schritten. |
...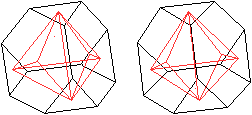 ... ... |
Verbinde die Mittelpunkte jedes Sechsecks links und
rechts mit den drei Mittelpunkten der benachbarten Dreiecke.
Man erkennt zwei aufgesetzte Dreieckspyramiden. |
...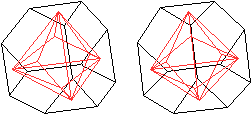 ... ... |
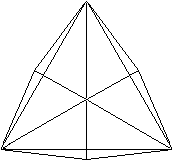
Verbinde die Mittelpunkte der Sechsecke hinten und
unten mit den drei Mittelpunkten der benachbarten Dreiecke.
Das Triakistetraeder ist komplett. |
...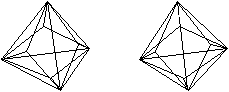 ... ... |
Man kann das erzeugende, abgestumpfte Tetraeder außen
weglassen. |
Bei Dualität gelten
die folgenden Aussagen:
>Die Anzahl der Seitenflächen und die der Eckpunkte
tauschen sich aus.
>Die Anzahl der Kanten bleibt gleich.
>Das abgestumpfte Tetraeder
hat 8 Seitenflächen. Dann hat das Triakistetraeder 12 Seitenflächen.
>Das abgestumpfte Tetraeder hat 12 Eckpunkte. Dann hat
das Triakistetraeder 8 Eckpunkte.
>Das abgestumpfteTetraeder hat 18 Kanten. Dann hat das
Triakistetraeder auch 18 Kanten.
Dritte Annäherung
top
... ... ... |
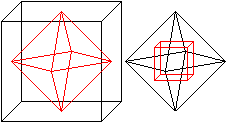
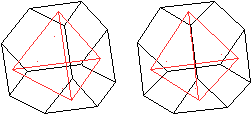
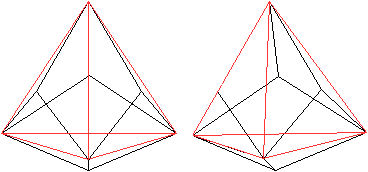
Oben wurde gezeigt, dass sich ein (rotes) Tetraeder ergibt,
wenn man die Mittelpunkte der Dreiecke eines abstumpften Tetraeders miteinander
verbindet. |
...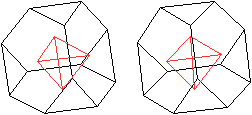 ... ... |
Wenn man die Mittelpunkte der Sechsecke eines abstumpften
Tetraeders miteinander verbindet, ergibt sich ein (kleineres) Tetraeder. |
...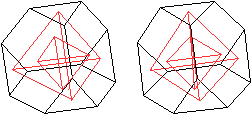 ... ... |
Beide zusammen bilden einen Körper aus zwei sich
durchdringenden Tetraedern. |
...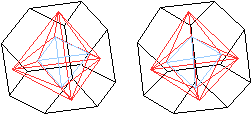 ... ... |
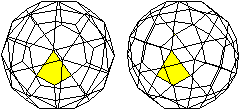
Das Triakistetraeder ist der Körper, der um beide
Tetraeder herum liegt.
Das kleine Tetraeder im Inneren ist in dieser Zeichung
jetzt blau. |
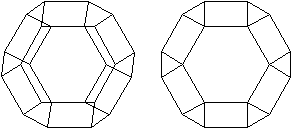
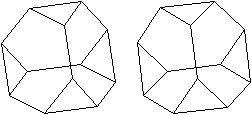
Zwei
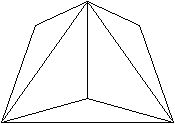
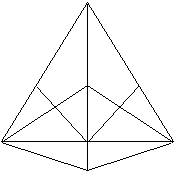
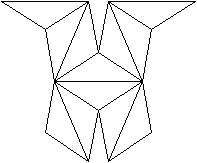
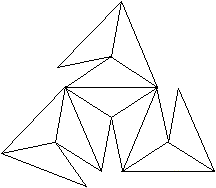
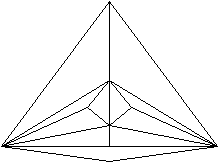
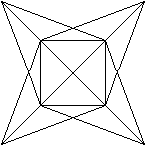
Netze und zwei Schlegel-Diagramme top
Besondere
Ansichten top
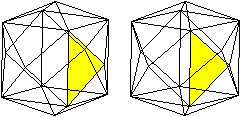
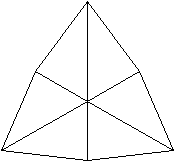
1
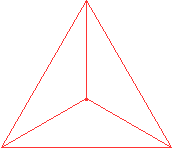
Erzeugendes Tetraeder
|
durchsichtig
|
undurchsichtig
|
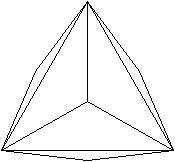
undurchsichtig
|
Die Verbindungslinie eines Punkte mit
3 Kanten und eines Punktes mit 6 Kanten liegt senkrecht zur Zeichenebene
und erscheint somit als Punkt.
2
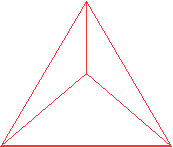
Erzeugendes Tetraeder
|
durchsichtig
|
undurchsichtig
|
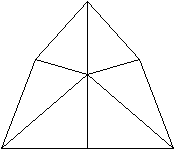
Die Seitenfläche unten steht senkrecht zur Zeichenebene
und erscheint als Strecke.
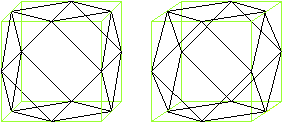
3
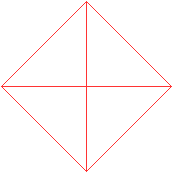
Erzeugendes Tetraeder
|
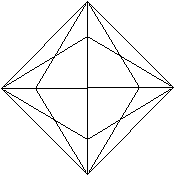
durchsichtig
|
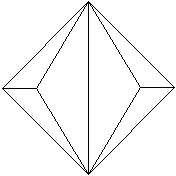
undurchsichtig
|
Das erzeugende Tetraeder erscheint als Quadrat mit seinen
Diagonalen.
4
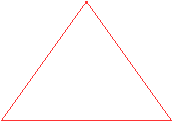
Erzeugendes Tetraeder
|
durchsichtig
|

oder undurchsichtig
|
Oben liegen zwei Eckpunkte, von denen 6 Kanten ausgehen,
hintereinander.
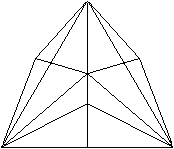
5
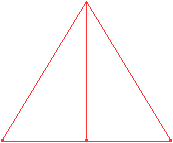
Erzeugendes Tetraeder
|
durchsichtig
|
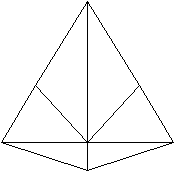
undurchsichtig
|
Drei Eckpunkte, von denen 6 Kanten ausgehen, liegen in der
Projektion auf einer Geraden.
Größen
top
Formeln
Das Triakistetraeder wird i.a.
durch die lange Kante a festgelegt. Dann lassen sich daraus die
Größen kurze Kante b, Volumen
V, Oberfläche
O,
Höhe
k der aufgesetzten Pyramide und Radius r der Inkugel
wie folgt berechnen.
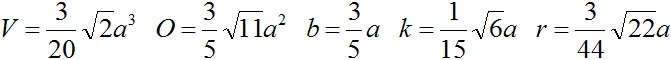
Für die Herleitung dieser
Formeln werden die folgenden Formeln als bekannt vorausgesetzt.
Tetraeder:
Radius der Umkugel R''=(1/4)sqrt(6)a'',
Radius der Inkugel r''=(1/12)sqrt(6)a'', V=(1/12)sqrt(2)a'', Höhe
H=(1/3)sqrt(6)a'', Abstand zweier windschiefer Kanten: c=(1/2)sqrt(2).
Abgestumpftes
Tetraeder: Radius der Umkugel R'=(1/4)sqrt(22)a', Radius der
Inkugel r'=(3/4)sqrt(26)a',
Abstand der Mitte vom Dreiecks
r3=(5/12)sqrt(6)a'¸ Abstand der Mitte vom Sechseck r6=(1/4)sqrt(6)a'.
Herleitungen
top
Kurze Kante b
Die kurze Kante b ist die Verbindungsstrecke der Mittelpunkte
eines Dreiecks und eines Sechsecks des erzeugenden Tetraederstumpfes.
... ... ... |
...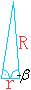 ... ... |
Im roten Tetraeder gilt für
den Winkel zwischen dem Radius der Umkugel und der Inkugel cos(beta) =
r/R = [(1/12)sqrt(6)a'']:[(1/4)sqrt(6)a''] = 1/3.
|
... |
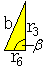 |
Nach dem Kosinussatz gilt b²
= r3²+r6²-2r3r6cos(beta). |
b² = r3²+r6²-2r3r6cos(beta)
= [(5/12)sqrt(6)a']²+[(1/4)sqrt(6)a']²-2[
5/12)sqrt(6)a'] [(1/4)sqrt(6)a'](1/3) = (25/24)a'²+(3/8)a'²-(10/24)a'²
= a'².
Also ist b=a'.
Die lange Kante a steht in
folgender Beziehung zur Kante a' des erzeugenden Tetraeders.
Die Kante a ist die Verbindungsstrecke der Mittelpunkte
zweier Dreiecke des erzeugenden Tetraederstumpfes.
...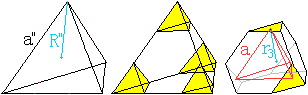 ... ... |
Das erzeugende Tetraeder des Tetraederstumpfes
und das erzeugende Tetraeder des Triakistetraeders sind ähnlich, so
dass gilt
a'':R''=a:r3= oder a''r3=R''a
oder a''[(5/12)sqrt(6)a']=(1/4)sqrt(6)a''a oder (5/12)a’=(1/4)a oder a'=(3/5)a. |
Also ist b=a'=(3/5)a
Höhe
k der aufgesetzten Pyramide
... ... ... |
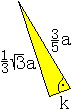 ... ... |
Die Höhe der Dreieckspyramide taucht als Kathete
in einem rechtwinkligen Dreieck mit der kurzen Seite b=(3/5)a und
dem längeren Abschnitt der Seitenhalbierenden eines gleichseitigen
Dreiecks auf. Er hat die Darstellung (1/3)sqrt(3)a.
Nach dem Satz des Pythagoras gilt k²
= (3/5a)²-[(1/3)sqrt(3)a]².
Dann ist k² = (9/25)a²-(1/3)a²
= (27/75)a²-(25/75)a² = (2/75)a² = (6/225)a².
Daraus folgt k = (1/15)sqrt(6)a. |
Volumen
V
... ... ... |
Für das Volumen addiert man die Volumina des erzeugenden
Tetraeders und der 4 aufgesetzten Dreieckspyramiden. |
V = 4*(1/3)[(1/4)sqrt(3)a²][(1/15)sqrt(6)a]+(1/12)sqrt(2)a³
= (1/15)sqrt(2)a³+(1/12)sqrt(2)a³
= (4/60)sqrt(2)a³+(9/60)sqrt(2)a³
= (3/20)sqrt(2)a³
Oberfläche
O
..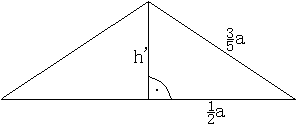 .... .... |
Das Triakistetraeder wird von 12 kongruenten, gleichschenkligen
Dreiecken mit den Seitenlängen a und b=(3/5)a gebildet.
Für die Höhe gilt h'² = [(3/5)a]²-[(1/2)a]²
= (9/25)a²-(1/4)a² = (11/25)a².
Dann ist h' = (1/10)sqrt(11)a. |
Dann ist O = 12*[(1/2)a(1/10)sqrt(11)a]
= (12/20)sqrt(11)a² = (3/5)sqrt(11)a²
Radius
r der Inkugel
...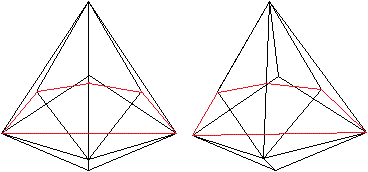 ... ... |
Man legt durch das Triakis-Tetraeder
eine Schnittfläche, in der die Inkugel als Kreis erscheint. |
...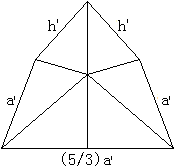 ... ... |
Die Schnittlinie ist ein Fünfeck
aus den Strecken h', h', a', a' und (5/3)a',
(5/3)a'.
Es ist für die Rechnung günstig,
vorerst die Seitenlänge a' des abgestumpften Tetraeders beizubehalten. |
...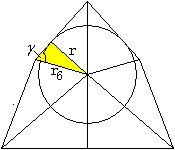 ... ... |
Man zeichnet den Kreis ein.
Der Radius r ist Kathete eines
rechtwinkligen Dreiecks mit der Hypotenuse r6.
Die Strecke r6 ist der
Abstand des Mittelpunktes des Sechsecks vom Mittelpunkt des Tetraederstumpfes.
Führt man den Winkel gamma
ein, so gilt sin(gamma)=r/r6 oder r=r6*sin(gamma).
Es gilt, den Winkel gamma zu bestimmen. |
...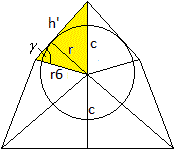 ... ... |
Dazu betrachtet man das größere
Dreieck mit den Seiten c, h' und r6.
Die Strecke 2c ist der Abstand
zweier windschiefer Kanten eines Tetraeders.
Es gilt 2c=(1/2)sqrt(2)(5/3)a'=(5/6)sqrt(2)a'
oder c=(5/12)sqrt(2)a'.
Die Seite h' ist die Höhe
einer Seitenfläche des Triakistetraeders.
Es gilt h'= (1/10)sqrt(11)a
= (1/10)sqrt(11)*(5/3)a' = (1/6)sqrt(11)a'.
Schließlich ist r6=(1/4)sqrt(6)a'. |
Nach dem Kosinussatz gilt
c²=r6²+h'²-2r6h'cos(gamma).
Dann ist
...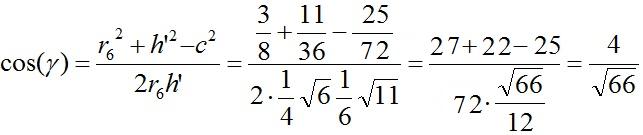
Weiter
...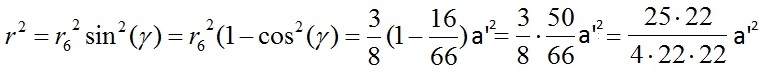
Dann ist r=(5/44)sqrt(22)a'==(5/44)sqrt(22)(3/5)a=(3/44)sqrt(22)a.
"Gekrönte" Tetraeder
top
Triakistetraeder
.. .... .... |
Das Triakistetrader wird auf dieser Seite als ein Tetraeder
vorgestellt, auf dessen Seitenflächen dreiseitige Pyramiden der Höhe
k=(1/15)sqrt(6)a (oder gerundet 0,16a) liegen. |
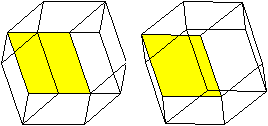
Würfel
...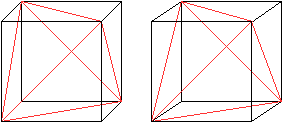 ... ... |
Wächst die Höhe der aufgesetzten Dreieckspyramiden
weiter, so wird der Zustand erreicht, bei dem zwei aneinander stoßende
Dreiecke in einer Ebene liegen.
Der Körper artet zu einem Würfel aus.
Die Höhe der Dreieckspyramide ist (1/6)sqrt(6)a
(oder gerundet 0,40a). |
Hypertetraeder
... ... ... |
Wächst die Höhe weiter, so wird der Körper
konkav und zu einem Stern.
Markant ist er, wenn die aufgesetzten Pyramiden wie die
erzeugende Pyramide auch Tetraeder sind.
Die Höhen sind dann h=(1/3)sqrt(6) (oder gerundet
0,82a).
Er ist dadurch bekannt, dass er ein Netz des vierdimensionalen
Tetraeders, des Hypertetraeders, ist.
|
Weitere Catalan-Körper
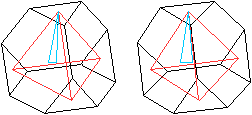
top
Auf meiner Webseite Archimedische
Körper findet man Stereo-Bilder aller catalanischen Körper.
Drei Beispiele
05 Abgestumpftes Oktaeder
und Hexaederstumpf
08 Kuboktaeder und Rhombendodekaeder
11 Kleines Rhombenikosidodekaeder
und Deltoidalhexakontaeder
Duale der platonischen
Körper
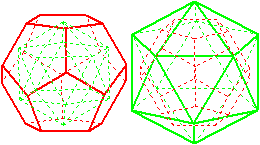
Die folgenden Zeichnungen zeigen, dass die dualen Körper
der platonischen Körper "unter sich bleiben".

Triakistetraeder
im Internet top
Deutsch
3D-Meier
Triakistetraeder
Mark Holtkamp (Mineralienatlas)
Triakistetraeder
Wikipedia
Triakistetraeder,
Tetraederstumpf,
Catalanischer
Körper, Archimedische
Körper
Englisch
Eric W. Weisstein (MathWorld)
Triakis
Tetrahedron, Triakis
Tetrahedral Graph, Catalan
Solid, Archimedean
Dual, Dual
Polyhedron,
Net
for the Triakis Tetrahedron (.pdf file)
Wikipedia
Triakis
tetrahedron, Truncated
tetrahedron, Catalan
solid, Archimedean
solid,
Truncated
triakis tetrahedron
Xplore & Xpress
Template
for triakis tetrahedron
Französisch
Robert FERRÉOL (ENCYCLOPÉDIE DES FORMES
MATHÉMATIQUES REMARQUABLES)
TRIAKI-TÉTRAÈDRE,
TÉTRAÈDRE
TRONQUÉ, POLYÈDRE
DE CATALAN,
DUAL
D'UN POLYÈDRE,
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2012 Jürgen Köller
top |
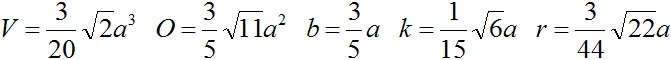
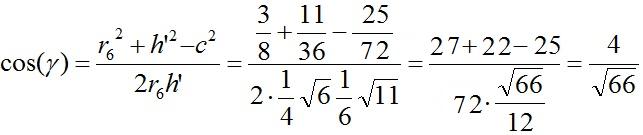
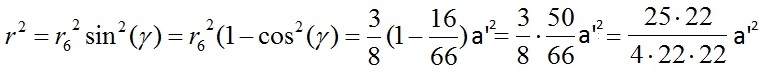

 ...
...

 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
...















 ...
...
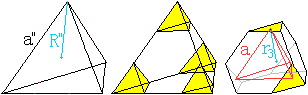 ...
... ...
... ...
... ....
.... ...
... ...
... ...
... ...
... ...
... ...
...