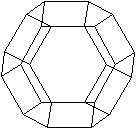
|
Was ist ein abgestumpftes Oktaeder?
... ...
|
Ein abgestumpftes Oktaeder
ist ein Körper, der von 8 regelmäßigen Sechsecken und 6
Quadraten gebildet wird.
Da an jeder Ecke regelmäßige Vielecke in gleicher
Weise aufeinandertreffen, gehört es zu den archimedischen Körpern. |
Das abgestumpfte
Oktaeder entsteht aus einem Oktaeder, indem man an den Ecken passend
quadratische Pyramiden abschneidet. Dazu teilt man alle Kanten des Oktaeders
in drei gleiche Teile.
... ... |
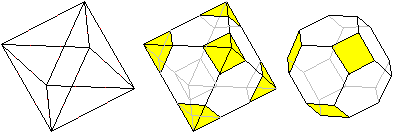An den sechs Ecken des Oktaeders entstehen bei diesem
Körper sechs Quadrate.
Die acht Dreiecke des Oktaeders reduzieren sich auf acht
Sechsecke. |
Neben den 6+8=14 Seitenflächen
hat das abgestumpfte
Oktaeder 36 Kanten und
24 Ecken.
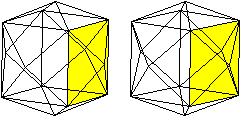
Die beiden folgenden, nebeneinander
liegenden Bilder ermöglichen eine dreidimensionale Ansicht des Körpers.
undurchsichtig:
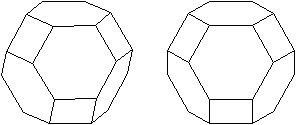durchsichtig:
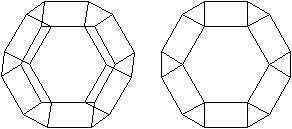
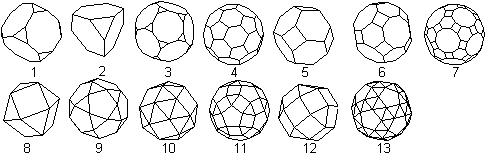Da beim Oktaederstumpf (5) an jeder Ecke regelmäßige
Vielecke in gleicher Weise aufeinandertreffen, gehört er zu den 13
archimedischen
Körpern.
Beschreibung top
Lage der Quadrate und Sechsecke
|
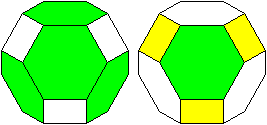
Drei Sechsecke und drei Quadrate umgeben ein Sechseck. |
|
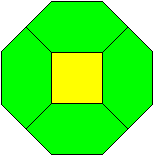
Vier Sechsecke umgeben ein Quadrat. |
| Es gibt vier Paare gegenüberliegender Sechsecke.
|
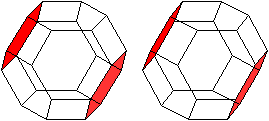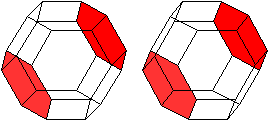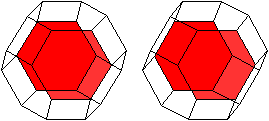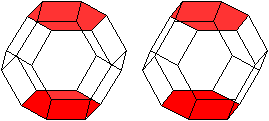
Es gibt drei Paare gegenüberliegender Quadrate.
|
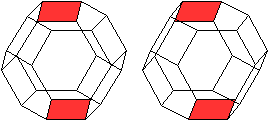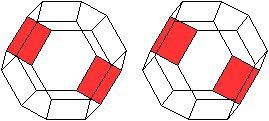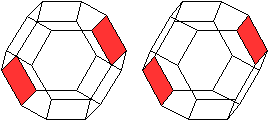
Parallelprojektionen
Ein Sechseck, ein Quadrat, eine Kante, eine Kante und
ein Eckpunkt liegen vorne.
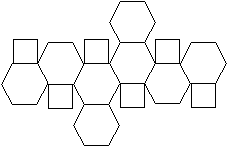
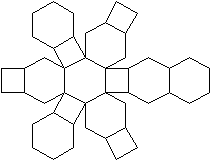
Netze
Schlegel-Diagramm
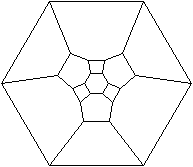
Diagonalen
84 Flächendiagonalen
..... . |
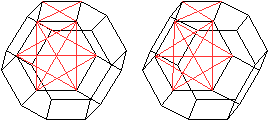Die Diagonalen der Sechsecke und der Quadrate bilden
die Flächendiagonalen des Oktaederstumpfes.
Das führt zu insgesamt 8*9+6*2=84 Flächendiagonalen. |
156
Raumdiagonalen
... ... |
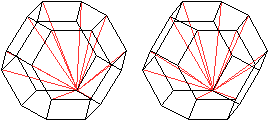Von jedem der 24 Eckpunkte gehen je 13 verschieden lange
Raumdiagonalen aus.
Das führt zu insgesamt (1/2)*24*13=156 Raumdiagonalen
des Oktaederstumpfes. |
Bilanz
Auf meiner Seite Dreieckszahlen
steht: "Verbindet man n Punkte mit allen möglichen geraden Linien,
so ergeben sich 1+2+3+...+(n-1)=(1/2)(n-1)n Strecken."
Für das abgestumpfte Oktaeder bedeutet das, dass
es (1/2)*23*24=276 Verbindungslinien gibt.
Das sind die 36 Kanten, 84 Flächendiagonalen und
156 Raumdiagonalen.
Größen top
Das abgestumpfte Oktaeder sei durch die Kantenlänge
a gegeben.
Daraus lassen sich die Größen Volumen V,
Oberfläche O, Radius R der Umkugel, Abstand r4
eines Quadrats vom Mittelpunkt des Oktaederstumpfes und Abstand r6
eines Sechsecks vom Mittelpunkt berechnen.
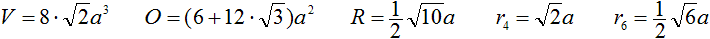
Herleitungen
Volumen
V
Vorweg: Für das Oktaeder mit Kantenlänge a'
gilt h' = (1/2)sqrt(2)a' und V' = (1/3)sqrt(2)a'³.
... ... |
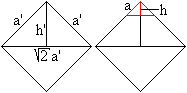Für die quadratische Pyramide, die man abschneidet,
gilt h=(1/3)h'= und a=a'/3
und weiter Vp = (1/3)a²h = (1/3)a²(h'/3)
= (1/6)sqrt(2)a³. |
Man erhält das Volumen des abgestumpften Oktaeders,
indem man das sechsfache Volumen der abgeschnittenen Pyramide vom Volumen
des Oktaeders subtrahiert.
V = V'-6Vp = (1/3)sqrt(2)a'³ - 6*(1/6)sqrt(2)a³
= 9sqrt(2)a³ - 6*(1/6)sqrt(2)a³ = 8sqrt(2)a³
Oberfläche
O
Die Oberfläche setzt sich aus sechs Quadraten und
der acht regelmäßigen Sechsecke zusammen.
O = 6a²+8[(3/2)sqrt(3)]a² = [6+12sqrt(3)]a²
Radius
R
der
Umkugel
... ...
|
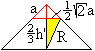Nach dem Satz des Pythagoras gilt R² = [(2/3)h']²+[(1/2)sqrt(2)a]²
= (5/2)a²
oder R = (1/2)sqrt(10)a. |
Abstand
r4
eines Quadrates vom Mittelpunkt
Der Abstand beträgt r4 = (1/2)sqrt(2)a'-(1/2)sqrt(2)a
= (3/2)sqrt(2)a-(1/2)sqrt(2)a = sqrt(2)a
Abstand
r6
eines Sechseckes vom Mittelpunkt
Vorweg: Der Radius der Inkugel im Oktaeder der Kantenlänge
a' ist r = (1/6)sqrt(6)a'.
Dann ist r6 = (1/6)sqrt(6)(3a) = (1/2)sqrt(6)a.
Winkel
zwischen zwei Seitenflächen
Der Winkel zwischen zwei Sechsecken beträgt 125°15'.
Der Winkel zwischen Quadrat und Sechseck beträgt
109°28'.
Quelle (1)
Raumausfüllung top
 |
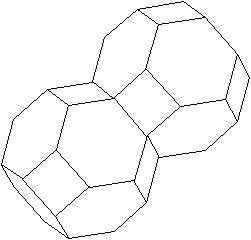Es ist bekannt, dass Würfel den Raum lückenlos
ausfüllen.
Es ist erstaunlich, dass auch abgestumpfte Oktaeder den
Raum ausfüllen. |
Tensegrity Structure
top
Ich wähle für die folgende Anordnung die englische
Bezeichnung, da es offenbar kein deutsches Wort gibt.
Modell
... ...
|
Mein Beispiel für eine Tensegrity structure ist
das nebenstehende Gebilde aus 12 Stäben, die kunstvoll an den Enden
durch Schnüre miteinander verbunden sind.
Der Körper ist in sich stabil.
Im Inneren ist als Blickfang eine Glaskugel eingeschlossen.
|
... ...
|
Verbindet man die Endpunkte der Stäbe durch Linien,
so ergibt sich - leicht verfälscht - ein abgestumpftes Oktaeder. |
Hintergrund
In das unübersichtliche Gebilde kommt Ordnung, wenn
man im abgestumpften Oktaeder für jedes Sechseck-Paar drei Raumdiagonalen
einzeichnet.
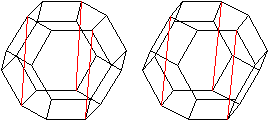
Da es, wie oben durch eine Animation veranschaulicht,
vier Paare von Sechsecken gibt, ergeben sich insgesamt 12 Raumdiagonalen.
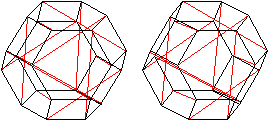
Die roten Linien sind die Stäbe, die schwarzen Begrenzungslinien
des abgestumpften Oktaeders sind Schnüre.
Zweite
Version
... ... |
Dieses ist eine Version, bei der die Schnüre durch
dünne Stäbe ersetzt sind, die durch Bohrungen der dickeren Stäbe
führen und sie in ihrer Lage halten.
Es wird als Denkspiel (schwer) verkauft:
Man soll die Kugel im Inneren befreien.
Im Moment (November 2007) wird es im Dänischen
Bettenhaus für 2,99 € verkauft. |
Mehr Informationen über
das interessante Thema Tensegrity kann man sich über die zahlreichen
Links meiner Linkliste unten holen.
Weitere Körper
top
Kuboktaeder
... ... |
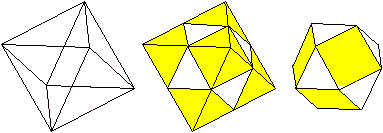Aus einem Oktaeder kann ein zweiter Körper auch
durch Abschneiden quadratischer Pyramiden entstehen. Dazu halbiert man
die Kanten.
Dieser Körper entsteht auch aus einem Würfel
durch die gleiche Prozedur. Er heißt Kuboktaeder. |
Tetrakishexaeder
Verbindet man die Mittelpunkte nebeneinander liegender
Mittelpunkte der Seitenflächen, so entsteht der duale Körper
des abgestumpften Oktaeders, das Triakistetraeder
oder der Pyramidenwürfel.
Er gehört zu den catalanischen
Körpern.
... ... |
Das Tetrakishexaeder setzt sich aus 24 gleichschenkligen
Dreiecken zusammen.
Er hat weiter 14 Ecken und 36 Kanten. |
Abgestumpftes
Oktaeder im Internet top
Deutsch
H.B.Meyer
Abgestumpftes
Oktaeder aus (sechs) Flechtstreifen
Wikipedia
Oktaederstumpf,
Archimedischer
Körper, Tensegrity,
Tensegrity
(Architektur), Tetrakishexaeder
Englisch
Eric W. Weisstein (MathWorld)
Truncated
Octahedron, Archimedean
Solid, Tensegrity
Geneviève Tulloue ( Figures Animées pour
la Physique )
Polyhedra
(Applets)
G. Korthals Altes
Paper
Models of Truncated Octahedron
H.B.Meyer
Truncated
Octahedron of six paper strips
Jaap Zonneveld's Stereoscopic show of Mathematical Models
Truncated
Octahedron (.gif picture)
Poly
A program
for downloading (Poly is a shareware program for exploring and constructing
polyhedra)
Die meisten Zeichnungen auf dieser Seite entstanden
mit Hilfe dieses Programmes.
Wikipedia
Truncated
octahedron,
Archimedean
solid, Tensegrity,
Bitruncated
cubic honeycomb,
Tetrakis
hexahedron
Französisch
Robert FERRÉOL
OCTAÈDRE
TRONQUÉ
Referenzen top
(1) H.Martyn Cundy and A.P.Rollett: Mathematical Models,
Oxford 1961 (Seite 104)
Feedback: Emailadresse
auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2007, überarbeitet 2013, Jürgen Köller
top |
