|
Was ist eine Evolute?
... ... ... |
Das wird an einem Beispiel erklärt.
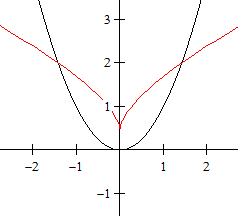
Gegeben ist die Normalparabel durch f(x) = x². Ihr
wird eine Kurve zugeordnet, die Evolute. Sie ist der geometrische Ort der
Mittelpunkte der Krümmungskreise der Parabel.
Für eine ausführlichere Erklärung muss
man weiter ausholen. |
Krümmung
einer ebenen Kurve top
Steigungsdreieck der Sekante
...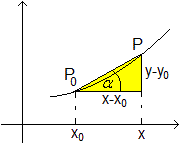 ... ... |
Gegeben seien der Graph der Funktion f durch die Gleichung
y=f(x) und ein fester Punkt P0(x0|y0)
auf ihm. Durch den Punkt P0 gehe eine Gerade, die den Graphen
auch in Punkt P(x|y) schneidet. Die Steigung dieser Sekante erfasst man
durch das Steigungsdreieck mit den Seiten y-y0 und x-x0.
Die Steigung ist ms= tan(alpha) = (y-y0)/(x-x0). |
... ... ... |
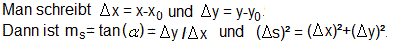 |
Steigungsdreieck
der Tangente
...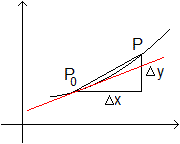 ... ... |
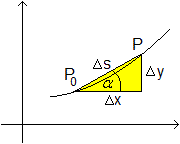
Interessant wird die Figur, wenn sich der Punkt P auf
den Punkt P0 zu bewegt. Ist P=P0, so ist die Sekante
zur Tangente geworden; der Winkel alpha wird Steigungswinkel der
Tangente. Das Steigungsdreieck der Sekante verschwindet und seine Seiten
werden zu Null. Die Steigung ist mt = 0/0 und nicht definiert,
andererseits weist die Zeichnung darauf hin, dass die Tangente eine Steigung
hat. Klärung bringt der Begriff des Grenzwertes. |
... ... ... |
Als Beispiel wird die Steigung der Tangente der Normalparabel
mit y=x² als Grenzwert bestimmt. Für die Sekante ist ms=
(y-y0 )/(x-x0) = (x²-x0²)/(x-x0)
= [(x+x0)(x-x0)]/(x-x0) = x+x0.
Dann ist mt = x0+x0 = 2x0.
Die Steigung der Tangente ist also das Doppelte des x-Wertes.
Ist die Funktionsgleichung f(x) = x², dann nennt
man die Zuordnung der Steigung zu einem x-Wert Ableitung der Funktion
und schreibt y' = f '(x) = 2x. |
...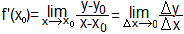 ... ... |
Allgemein ist die Ableitung einer Funktion f an einer
Stelle x0 gleich dem Grenzwert. |
...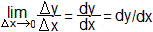 ... ... |
Es ist möglich, Grenzwerte mit Hilfe von Differentialen
zu schreiben. Mit ihnen kann man dann rechnen wie mit Variablen. |
Beispiel
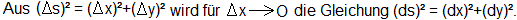
Krümmung
einer Kurve
Man definiert für die Kurve
zu y = f(x) die Krümmung als k=(d alpha)/ds.
Der Term (d alpha)/ds wird umgeformt.
Durch Erweitern erhält man
(d alpha)/ds = [(d alpha)/dx]/[ds/dx].
Für (d alpha)/dx schreibt man:
Es gilt dy/dx = y' = f '(x) = tan(alpha)
und weiter nach der Kettenregel
y'' = f ''(x) = d2y/(dx)²
= [1+tan(alpha)][(d alpha)/dx)]
= [1+(dy/dx)²][(d alpha)/dx)]
Dann ist (d alpha)/dx = [d2y/(dx)²]/[1+(dy/dx)²].
Für ds/dx schreibt man:
Aus (ds)² = (dx)²+(dy)²
folgt (ds)²/(dx)² =1+(dy)²/(dx)² oder (ds)/(dx) =sqrt
[1+(dy/dx)²].
Zusammengefasst:
Für die Krümmung k =
(d alpha)/ds = [d2y/(dx)²]/[ds/dx] ergibt sich dann
k = [d2y/(dx)²]/[1+(dy/dx)²]/[sqrt
[1+(dy/dx)²] = {[d2y/(dx)²]/[1+(dy/dx)²]3/2
oder ohne Differentiale übersichtlicher
geschrieben k = y''/(1+y'²)3/2.
Diese Formel gilt für Kurven
von Funktionen, die zweimal differenzierbar sind.
Krümmung des Kreises top
...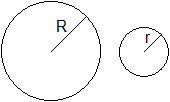 ... ... |
Gegeben sind zwei Kreise mit den Radien R und r.
Man sagt: Der große Kreis ist weniger gekrümmt
als der kleine.
Als ein Maß für die Krümmung sind die
reziproken Radien geeignet.
Man definiert: Der große Kreis hat die Krümmung
k1 = 1/R, der kleine k2 = 1/r.
Da in diesem Falle R=2r gilt, hat der kleine Kreis die
doppelte Krümmung wie der große, k2 = 2k1. |
Hat ein Kreis z. B. den Radius r=5 cm, so ist seine Krümmung
k = 1/5 (1/cm) = 0,2 (1/cm).
Es soll gezeigt werden, dass
die Formel k = y''/(1+y'²)3/2 eine
Verallgemeinerung von k=1/r ist oder - anders ausgedrückt - dass k
= 1/r ein Sonderfall ist.
Nachweis
Es gilt für den Kreis x²+y²=1, abgeleitet
2x+2yy ' = 0 oder
(*) x+yy ' = 0, noch einmal abgeleitet
(**) 1+yy ''+y '² = 0.
Aus (*) folgt y ' = -x/y und 1+y'² =1+x²/y²
= (y²+x²)/y².
Aus (**) folgt y '' = - (1+y '²)/y = - (1+x²/y²)/y
= - (x²+y²)/y³.
Dann ist k = y''/(1+y'²)3/2
= - [(x²+y²)/y³]/[(y²+x²)/y²]3/2
= - (x²+y²)-1/2 = -1/r.
Ergebnis
Bis auf das Vorzeichen ist k = 1/r als Sonderfall bestätigt.
Positive
oder negative Krümmung
Und was bedeutet das Vorzeichen in k= - 1/r? Dazu betrachtet
man die Halbkreise oben und unten getrennt.
...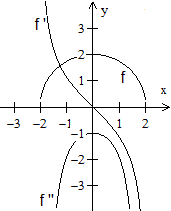 ... ... |
Der obere Halbkreis wird durch die Funktionsgleichung
y=sqrt(4-x²) beschrieben.
Die ersten beiden Ableitungen sind y ' = (-2x)/sqrt(4-x²)
und y '' = -(8+2x²)/(4-x²)3/2.
Die zweite Ableitung ist negativ. Bekanntlich beschreibt
ein Graph einer Funktion eine Rechtskurve, wenn die zweite Ableitung negativ
ist. Das ist hier der Fall.
Offenbar bestimmt in k = y''/(1+y'²)3/2
die zweite Ableitung, ob die Krümmung k positiv oder negativ ist.
Das führt zu folgender Aussage:
Ist die Krümmung k eines Kreises
negativ, so beschreibt der Kreis eine Rechtskurve. |
...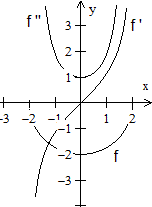 ... ... |
Der untere Halbkreis wird durch die Funktionsgleichung
y=-sqrt(4-x²) beschrieben.
Die ersten beiden Ableitungen sind y ' = (2x)/sqrt(4-x²)
und y '' = (8+2x²)/(4-x²)3/2.
Die zweite Ableitung ist positiv.
Der Graph einer Funktion beschreibt eine Linkskurve,
wenn die zweite Ableitung positiv ist.
Das führt zu folgender Aussage:
Ist die Krümmung k eines Kreises
positiv, so beschreibt der Kreis eine Linkskurve. |
Resümee
Die Krümmung eines Kreises ist nach diesen Überlegungen
1/r oder -1/r. Es ist aber sinnvoll, dem Kreis die positive Zahl 1/r zuzuordnen.
Man löst diese Problematik, indem man die Krümmung
einer Kurve bei Bedarf auch mit k = |y''|/(1+y'²)3/2
definiert.
Dabei ist |y''| der Betrag der
zweiten Ableitung. Dabei verzichtet man auf eine Aussage über die
Krümmungsart.
Krümmungskreis
einer Kurve top
Die Krümmung einer Kurve in
einem Punkt beschreibt man durch den Krümmungskreis. Das ist
der Kreis, der die Kurve berührt. Kreis und Kurve haben die gleiche
Tangente und darüber hinaus die gleiche Krümmung. Der Mittelpunkt
der Krümmungskreises liegt auf der Normalen des Berührpunktes.
...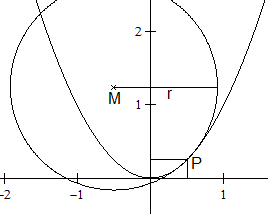 ... ... |
Das wird durch ein Beispiel veranschaulicht.
Gegeben sind die Normalparabel mit y=x², y'= 2x
und y''=2 und auf ihr der Punkt P(1/2|1/4).
Die Krümmung in P ist k= y''/(1+y'²)3/2
= 2/(1+1)3/2 = 2/sqrt(8) = 1/sqrt(2).
Der Radius des Krümmungskreises ist dann r = 1/k
= sqrt(2).
Im nächsten Abschnitt wird gezeigt, dass der Mittelpunkt
in M(-1/2|5/4) liegt.
Der Krümmungskreis wird also durch die Gleichung
(x+1/2)²+(y-5/4)² = 2 beschrieben. |
Koordinaten
des Mittelpunktes des Krümmungskreises
Für die Bestimmung des Mittelpunktes
des Krümmungskreises benötigt man folgende trigonometrische Formeln.
sin(alpha) = tan(alpha)/sqrt[1+tan²(alpha)]
und cos(alpha) = 1/sqrt[1+tan²(alpha)].
Gegeben sei der Graph der Funktion durch y = f(x) mit
den Ableitungen y' und y''. Der Steigungswinkel sei alpha.
Da y' = tan(alpha) gilt, gilt sin(alpha) = y'/sqrt(1+y'²)
und cos(alpha) = 1/sqrt(1+y'²).
...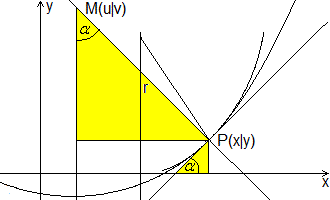 ... ... |
Ein fester Kurvenpunkt sei P(x|y) und der Mittelpunkt
des Krümmungskreises M(u|v).
Die beiden gelben Dreiecke sind ähnlich. Die gekennzeichneten
Winkel sind gleich, da die Schenkel paarweise aufeinander senkrecht stehen.
Es gilt u = x-r*sin(alpha) und v = y+r*cos(alpha). Weiter
ist r = 1/k = (1+y'²)3/2/y''.
Man setzt in die Gleichungen r, sin(alpha) und cos(alpha)
ein.
Das führt zu u = x-[(1+y'²)3/2/y'']*[y'/sqrt(1+y'²)]
und schließlich zu u(x) = x-y'(1+y'²)/y''.
Entsprechend gilt v(x) = y+(1+y'²)/y''. |
Evolute
Die Gleichungen sind eine Parameterdarstellung der Ortslinie
der Mittelpunkte M(u|v) der Krümmungskreise. Der Parameter ist x.
Die Ortslinie heißt Evolute.
Evolute der
Normalparabel top
Die Funktionsgleichung der Normalparabel ist y = x².
... ... ... |
Zur Bestimmung der Parameterform setzt man y = x²,
y' = 2x und y'' = 2 in u = x-y'(1+y'²)/y'' und v = y+(1+y'²)/y''
ein.
Dann ist u = x-2x(1+4x²)/2 = -4x³ und v=x²+(1+4x²)/2
= 1/2+3x².
Nennt man wie üblich den Parameter x=t und setzt
u=x und v=y, so wird die Evolute Parameterform
dargestellt durch
x = -4t³
y = 3t²+1/2.
|
Zur Koordinatengleichung gelangt man so.
Es gilt x2 = 16t6 und 3t²
= (y-1/2) oder 27t6 = (y-1/2)³.
Daraus folgt (1/16)x² = (1/27)(y-1/2)³ oder
(27/16)x²
= (y-1/2)³.
Die Evolute ist eine Neilsche Parabel.
Oben wurde der Mittelpunkt
des Krümmungskreises im Punkte P(1/2|1/4) mit M(-1/2|5/4) angegeben.
Das kann jetzt bestätigt werden.
x = -4t³ = -4/8 = -1/2
y = 3t²+1/2 = 3/4+1/2 = 3/4+2/4 = 5/4
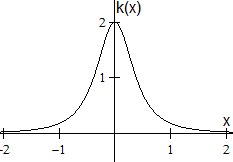
Von Interesse ist die Stelle x = 0 mit
der größten Krümmung.
... |
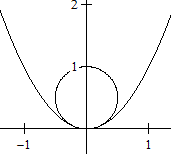 |
Es gilt k = y''/(1+y'²)3/2
= 2/(1+4x²)3/2.
Es gilt x = 4t³ = 0 und y = 3t²+1/2 = 1/2 |
Ergebnis
Der Mittelpunkt des Krümmungskreises liegt in M(0|1/2),
der Radius ist r=1/2 und die Krümmung k = 2.
Auf der Webseite https://de.wikipedia.org/wiki/Evolute
(URL unten) findet man eine Zeichnung, in der für viele Kurvenpunkte
die Krümmungskreise eingezeichnet werden. So kann man die Entstehung
der Evolute nachvollziehen.
Evolute der Ellipse
top
Es ist vom Rechenaufwand her günstig,
die Ellipse durch die Parameterform zu beschreiben. Sie lautet
x(t) = a cos(t)
y(t) = b sin(t).
Die Evolute soll auch in
Parameterform dargestellt werden.
Aus den Gleichungen u(x) = x-y'(1+y'²)/y'' und v(x)
= y+(1+y'²)/y'' wird
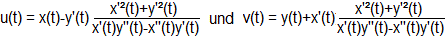
Herleitung
x=x(t)
y=y(t)
y' = dy/dx = (dy/dt)/(dx/dt) = y'(t)/x'(t)
y'' = (d/dx) y' = [d/dt)y']*[dt/dx ] = (d/dt)[y'(t)/x'(t)][1/x'(t)]
= {[x'(t)y''(t)-x''(t)y'(t)]/x'²(t)}[1/x'(t)] =
[x'y''-x''y']/x'³
1+y'² = 1+(y'²/x'²)
= (x'²+y'²)/x'²
Eingesetzt
u(t) = x-(y'/x')[(x'²+y'²)/x'²]/[x'y''-x''y']/x'³
= x-y'(x'²+y'²)/[x'y''-x''y']
v(t) = y+[(x'²+y'²)/x'²]/[(x'y''-x''y')/x'³]=y+x'[(x'²+y'²)/[(x'y''-x''y')]
Aus Gründen der besseren Lesbarkeit habe ich in
den blau markierten Termen den Zusatz (t) weggelassen.
Zurück zur Ellipse.
Für sie gilt x(t) = a cos(t),
x'
= -a sin(t) und x''
= -a cos(t).
und y(t) = b sin t, y' = b cos(t)
und y'' = -b sin(t).
Dann ist x'²+y'² =
a² sin²(t)+b² cos²(t) und
x'y''-x''y' = a sin(t) b
sin(t)+a cos(t) b cos(t) = ab[sin²(t)+cos²(t)] = ab.
Die Terme für u(t) und v(t) sind dann
u(t) = a cos(t)-b cos(t)[a² sin²(t)+b²
cos²(t)]/(ab)
= a cos(t)-(1/a) cos(t)[ a²-a²cos²(t)+b²cos²(t)]
= a cos(t)-a cos(t)+a cos³(t)-(b²/a)cos³(t)
= (a-b²/a)cos³(t) = [(a²-b²)/a]cos³(t)
v(t) = b sin(t)-a sin(t)[a² sin²(t)+b²
cos²(t)]/ab
= b sin(t)-(1/b) sin(t)[a² sin²(t)+b²-b²
sin²(t)]
= b sin(t) - (a²/b) sin³(t)-b sin(t)+b sin³(t)
= - (a²/b) sin³(t)+b sin³(t) = [(b²-a²)/b]sin³(t)
Ergebnis
Hat die Ellipse die Darstellung x(t)
= a cos(t) und y(t) = b sin (t),
so gilt für die Evolute u(t)
=
[(a²-b²)/a]cos³(t) und v(t) = [(b²-a²)/b]sin³(t).
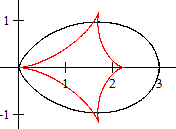
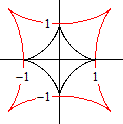
Das sind Parameterdarstellungen einer schiefen Astroide.
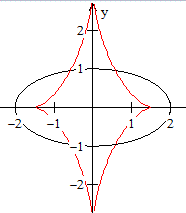
Zahlenbeispiel
...
|
Es sei a=2 und b=1.
Die Ellipsengleichung ist x(t)
= 2 cos(t) und y(t) = sin(t).
Die Evolutengleichung ist u(t)
= (3/2) cos³(t) und v(t) = -3 sin³(t). |
Besondere
Krümmungskreise
...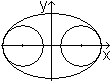 ... ... |
In den Hauptscheitelpunkten der Ellipse links sind zwei
Kreise eingezeichnet, die die Ellipse in diesen Punkten gut annähern.
Die Radien sind r=b²/a. |
Weitere
Evoluten top
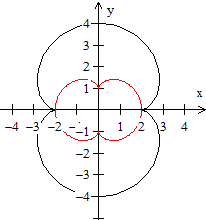
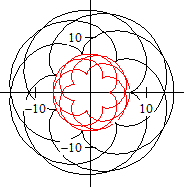
Nephroide: x=6cos(t)-4cos³(t), y=4sin³(t)
|
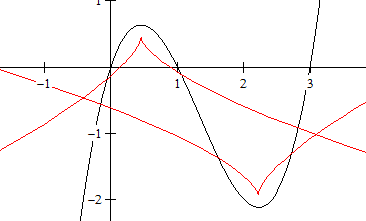
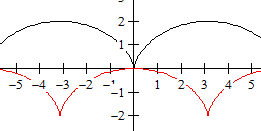
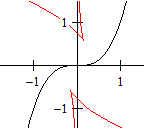
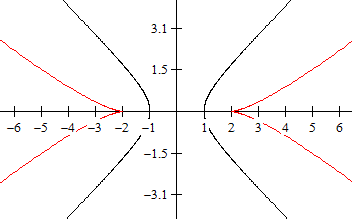
f(x) = x(x-1)(x-3)
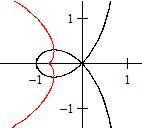
|
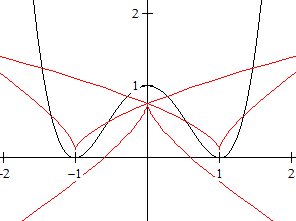
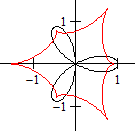
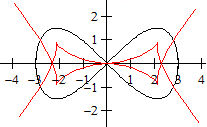
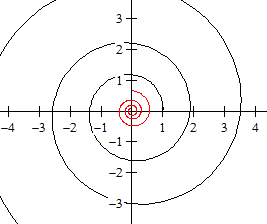
f(x) = (x+1)²(x-1)²
|
Mehr Beispiele findet man
im Internet auf folgenden Webseiten.
- Auf der Webseite https://de.wikipedia.org/wiki/Evolute
findet man Evoluten bekannter Kurven.
- Auf der Webseite Famous Curves Index
(URL unten) kann man die Evoluten vieler Kurven aufrufen.
- Das Programm Winplot, das ich für diese Seite
verwende, zeigt zu Funktionen die Evoluten an (Eine/Evolute.../Zeichnen).
Die Evolute
als Einhüllende top
Es folgt ein zweiter Zugang zur Evolute. Das wird am
Beispiel der Normalparabel erklärt.
...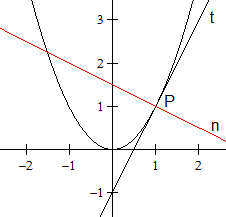 ... ... |
> Zeichne die Normalparabel mit f(x) = x².
> Zeichne in Punkt P(1|1) die Tangente t.
> Zeichne durch diesen Punkt P(1|1) die Senkrechte zur
Tangente. Das ist die Normale n.
Die Gleichungen sind t(x) = 2x-1 und n(x) = -(1/2)x+3/2. |
...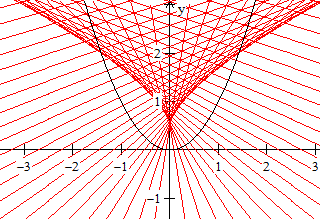 ... ... |
Zeichne zu hinreichend vielen Punkten P(x|y) die Normale.
Die Normalen na
formen
eine "Einhüllende". Diese Kurve ist die Evolute.
Umgekehrt sind die Normalen Tangenten der Evolute.
Die Parametergleichung ist na
(x) = -1/(2a)x+1/2+a² mit -2<a<2
und der Schrittlänge 50. |
... ... ... |
Das ist noch einmal die Evolute. |
Verallgemeinerung
Zu einer beliebigen Kurve zeichnet man durch die Kurvenpunkte
Normale. Die Normalen bilden eine Hüllkurve. Das ist die Evolute.
Auf der Webseite der Universität
Heidelberg (URL unten) findet man ab Seite 17 einen Beweis, dass die Evolute
auch eine von den Normalen „eingehüllte” Kurve ist.
Evolute im Internet
top
Deutsch
Wikipedia
Evolute,
Krümmungskreis,
Einhüllende,
Englisch
Arbeitsblätter Geogebra
Evolute
of a parabola
Eric W. Weisstein (MathWorld)
Evolute,
Involute,
Circle
Involute
Frederick Hartmann and Robert Jantzen
Apollonius's
Ellipse and Evolute Revisited - The Alternative Approach to the Evolute
Richard Parris (Freeware-Programme)
winplot
Wikipedia
Evolute
Feedback: Emailadresse auf meiner Hauptseite
URL meiner Homepage:
http://www.mathematische-basteleien.de/
© April 2016 Jürgen
Köller
top |
 ...
... ...
... ...
... ...
...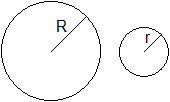 ...
...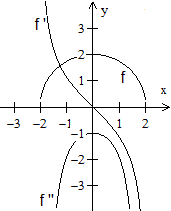 ...
...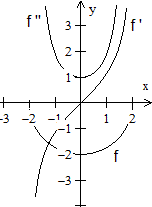 ...
...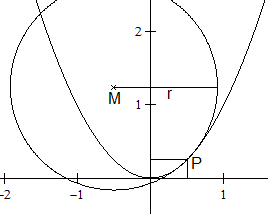 ...
... ...
...
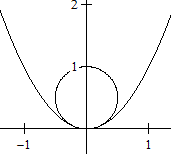

 ...
...
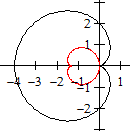



 ...
... ...
...