|
Was ist eine Epizykloide?
...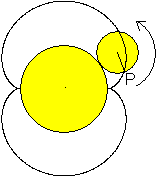 ... ... |
Gegeben sei ein (erzeugender) Kreis mit dem Radius R.
Rollt man einen zweiten Kreis mit dem Radius r auf ihm ab und verfolgt
man dabei die Bahn eines Punktes P auf der Kreislinie, so entsteht die
Epizykloide.
In diesem Falle gilt R=2r oder 2pi*R=2*(2pi*r).
Dann ergibt sich eine einfach geschlossene Kurve, die
Nephroide. |
Die Kurve ist verwickelter, wenn
das Verhältnis R:r nicht mehr ganzzahlig ist.
...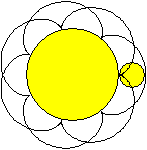 |
Ist das Verhältnis rational, schließt sich
die Kurve nach etlichen Umläufen.
Hier ist R:r=7:2. Die Kurve schließt sich nach zwei
Umläufen. |
...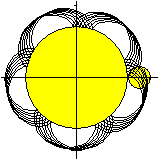 |
Ist das Verhältnis irrational wie z.B. bei R:r=7:sqrt(2),
schließt sich die Kurve nicht. |
Eine Eigenschaft ist diesen
Epizykloiden gemeinsam: Sie liegen in einem Kreisring, der von dem erzeugenden
Kreis mit dem Radius R und einem Hüllkreis mit dem Radius R+2r gebildet
wird.
Parameterdarstellung
der Epizykloide top
Die Epizykloiden auf dieser Seite werden mit Hilfe einer
Parameterdarstellung mit dem Programm Winplot gezeichnet. Die Formeln
lauten
x=(R+r) cos(t)-r cos[(1+R/r)t]
y=(R+r) sin(t)-r sin[(1+R/r)t]
Es gilt D=|R.
Herleitung der Formeln
...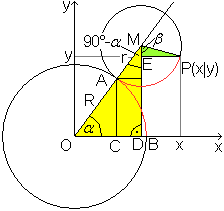 |
Wegen der Rollbedingung sind die Kreisbögen über
AB und AP gleich.
Es gilt b(AB)=(pi*alpha*R)/180° und b(AP)=[pi*(90°-alpha+beta)*r]/180°.
Daraus folgt alpha*R=(90°-alpha+beta)*r oder beta=(1+R/r)alpha-90°.
Im gelben Dreieck ODM gilt
sin(alpha)=MD/OM oder MD=(R+r)*sin(alpha) und
cos(alpha)=OD/OM oder OD=(R+r)*cos(alpha).
Im grünen Dreieck EPM gilt
sin(beta)=EP/MP oder EP=r*sin(beta)
cos(beta)=ME/MP oder ME=r*cos(beta) |
Weiter ist
x=OD+EP=(R+r)*cos(alpha)+r*sin(beta)=(R+r)*cos(alpha)+r*sin[(1+R/r)alpha-90°]
=(R+r)*cos(alpha)-r*cos[(1+R/r)alpha]
y=MD-ME=(R+r)*sin(alpha)-r*cos(beta)=(R+r)*sin(alpha)-r*cos[(1+R/r)alpha-90°]
=(R+r)*sin(alpha)-r*sin[(1+R/r)alpha].
Es ist üblich, die Winkel
im Bogenmaß anzugeben. Man setzt also alpha=t und erhält
x=(R+r) cos(t)-r cos[(1+R/r)t]
y=(R+r) sin(t)-r sin[(1+R/r)t].
Einfach
geschlossene Kurven top
Von Interesse ist die einfach geschlossene Kurve, die
sich ergibt, wenn das Verhältnis der Radien der beiden beteiligten
Kreise ganzzahlig ist. In diesem Falle setzt man gerne in die Parametergleichungen
R/r=m ein.
x=(R+r) cos(t)-r cos[(1+R/r)t]
y=(R+r) sin(t)-r sin[(1+R/r)t].
|
x=(m+1)r cos(t)-r cos[(m+1)t]
y=(m+1)r sin(t)-r sin[(m+1)t]
|
Beipiele
Kardioide
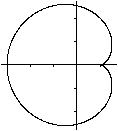
m=1
|
Nephroide
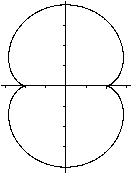
m=2
|
Dreistrahlige Epizykloide
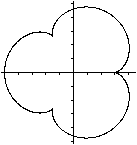
m=3
|
Vierstrahlige Epizykloide
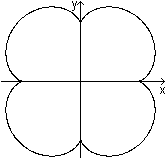
m=4
|
Fünfstrahlige Epizykloide
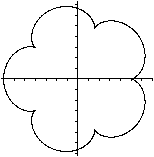
m=5
|
D={t | 0<=t<=2pi}
Beschreibung
der Kurven
..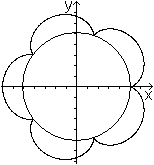 .... .... |
>Sie bestehen aus m kongruenten Bögen, die sich
über dem erzeugenden Kreis wölben.
>Für die Winkel 2(k-1)pi/m (1<=k>=m) ergeben
sich Spitzen, die auf dem Kreis mit dem Radius R liegen.
>Für die Winkel 2[(k-1)/2]pi/m (1<=k>=m) ergeben
sich Scheitel, die auf einem Kreis mit den Radius R+2r liegen.
>Die nebenstehende Epizykloide wird dargestellt durch
x=6cos(t)-cos(6t)
y=6sin(t)-sin(6t)
|
Flächeninhalt
und Umfang top
Es stellt sich für die einfach geschlossene Epizykloide
die Frage nach dem Flächeninhalt und dem Umfang.
Kardioide
Auf meiner Seite Herzkurve stelle
ich dar, wie man sie für die Kardioide (m=1) bestimmt.
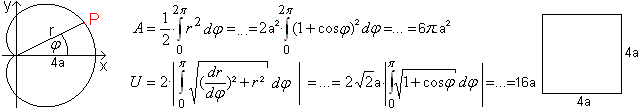 Dieses Verfahren lässt sich nicht verallgemeinern, da
es offenbar eine entsprechende Polargleichung der Epizykloide für
den allgemeinen Fall nicht gibt. (Bei Mathworld/Epicycloid findet
man eine Ersatzgleichung.)
Dieses Verfahren lässt sich nicht verallgemeinern, da
es offenbar eine entsprechende Polargleichung der Epizykloide für
den allgemeinen Fall nicht gibt. (Bei Mathworld/Epicycloid findet
man eine Ersatzgleichung.)
Allgemeine
Formeln
In der Literatur findet man die Formeln A=(m+1)(m+2)pi*r²
und U=8(m+1)r.
Anwendung auf einfache Epizykloiden
Kardioide
m=1
A=6pi*r²
U=16r
|
Nephroide
m=2
A=12pi*r²
U=24r
|
Dreistrahlige Epizykloide
m=3
A=20pi*r²
U=32r
|
Vierstrahlige Epizykloide
m=4
A=30pi*r²
U=40r
|
Fünfstrahlige Epizykloide
m=5
A=42pi*r²
U=48r
|
Andere Lesart der Formel
für den Flächeninhalt
...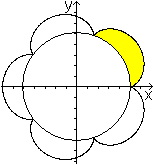 ... ... |
In Buch (3) findet man die Formel für die Fläche
zwischen dem erzeugenden Kreis und einem Bogen.
A'=pi*r²(3R+2r)/R.
Die Gesamtfläche ist dann
A=mA'+pi*R²=m[pi*r²(3R+2r)/R]=...=pi*r²(m²+3m+2)=(m+1)(m+2)pi*r²,
wie oben angegeben. |
Zur
Herleitung der Formel A=(m+1)(m+2)pi*r².
Für die Berechnung des Flächeninhalts steht
die Sektorformel von Leibniz bereit.
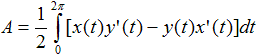
|
x(t)=(m+1)r cos(t)-r cos[(m+1)t]
y(t)=(m+1)r sin(t)-r sin[(m+1)t]
|
x'(t)=-(m+1)r sin(t)+r (m+1)sin[(m+1)t]
y'(t)=(m+1)r cos(t)-r (m+1)cos[(m+1)t]
|
Es gilt x(t)y'(t)-y(t)x'(t)
= (m+1)²r²[sin²(t)+cos²(t)]+(m+1)r²{sin²[(m+1)t]+cos²[(m+1)t]}
-[(m+1)²r²+(m+1)r²]{sin(t)sin[(m+1)t]+cos(t)cos[(m+1)t]}
=(m+1)²r²+(m+1)r²-[(m+1)²r²+(m+1)r²]cos(mt)
=[(m+1)²r²+(m+1)r²][1-cos(mt)]
=(m+1)(m+2)r²[1-cos(mt)]
Dann ist
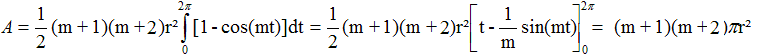 ,wzbw. ,wzbw.
Zur
Herleitung der Formel U=8(m+1)r
...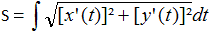 ... ...
|
Für die Länge eines Bogens steht die nebenstehende
Formel bereit. |
Es gilt [x'(t)]²+[y'(t)]²
={-(m+1)r sin(t)+r (m+1)sin[(m+1)t]}²+{(m+1)r cos(t)-r
(m+1)cos[(m+1)t]}²
=(m+1)²r²+(m+1)²r²-2(m+1)²r²{sin(t)sin[(m+1)t]+cos(t)cos[(m+1)t]}
=2(m+1)²r²-2(m+1)²r²cos(mt)
=(m+1)²r²[2-2cos(mt)].
Dann ist
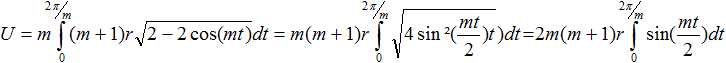
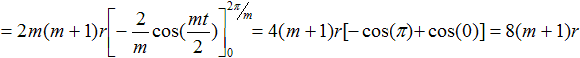 , wzbw. , wzbw.
Mehrfach
umlaufende Kurven top
Die Kurve ist verwickelter, wenn das Verhältnis
R:r nicht mehr ganzzahlig ist.
|
Ist das Verhältnis rational wie z.B. bei R:r=7:2,
schließt sich die Kurve nach etlichen Umläufen.
Die Parametergleichungen sind hier
x=9cos(t)-2cos[(9/2)t]
y=9sin(t)-2sin[(9/2)t]
D={t | 0<t<4pi}
|
Ist das Verhältnis R:r=p/q, wobei p und q teilerfremde
Zahlen sind, so schließt sich die Kurve nach q Umläufen.
Beispiele

R:r=7:1
D=[0;2pi]
|
R:r=7:2
D=[0;4pi]
|
R:r=7:3
D=[0;6pi]
|
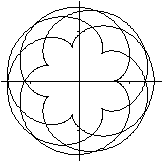
R:r=7:4
D=[0;8pi]
|
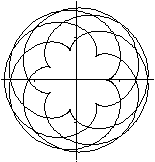
R:r=7:5
D=[0;10pi]
|
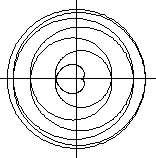
R:r=1:7
D=[0;14pi]
|
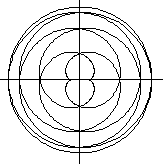
R:r=2:7
D=[0;14pi]
|
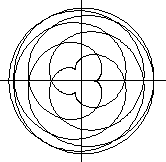
R:r=3:7
D=[0;14pi]
|
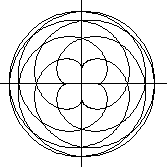
R:r=4:7
D=[0;14pi]
|
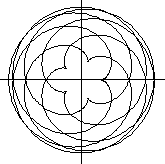
R:r=5:7
D=[0;14pi]
|
Nicht geschlossene
Kurven
top
... |
Ist das Verhältnis irrational wie z.B. bei R:r=7:sqrt(2),
schließt sich die Kurve nicht.
x=8.414cos(t)-1.414cos[8.414/1.414)t]
y=8.414sin(t)-1.414sin[(8.414/1.414)t]
0<t<14pi
|
Bögen wölben sich
über dem erzeugenden Kreis. Mit größer werdendem Parameter
verschieben sie sich entgegen dem Uhrzeigersinn. Das zeigt auch die folgende
Bildreihe.
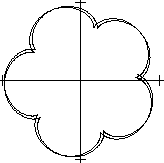
0<t<4pi
|

0<t<14pi
|
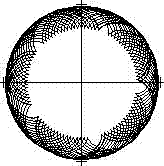
0<t<34pi
|

0<t<100pi
|
Epitrochoiden top
Gewöhnliche Epizykloide (oder
Gemeine E.)
...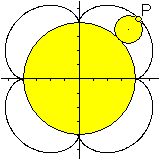 |
Bisher verfolgte man beim Abrollen einen Punkt P auf
der Kreislinie des abrollenden Kreises.
Es entsteht die gewöhnliche Epizykloide. |
Auch Punkte, die nicht auf
der Kreislinie liegen, beschreiben eine geschlossene Kurve, die Epitrochoide.
Da unterscheidet man, ob der Punkt P innerhalb oder außerhalb
des abrollenden Kreises liegt.
In beiden Fällen erfasst man die Kurven durch die
leicht abgeänderten Parametergleichungen von oben.
x=(R+r) cos(t)-a cos[(1+R/r)t]
y=(R+r) sin(t)-a sin[(1+R/r)t]
Die Variable a gibt die Entfernung des Punktes P vom Mittelpunkt
des abrollenden Kreises an. Bisher war a=r.
Gestreckte
Epizykloide (oder Verkürzte E.)
Der Punkt P liegt innerhalb des abrollenden
Kreises in der Entfernung a von seinem Mittelpunkt.
...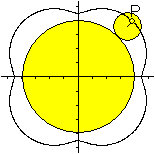 ...
a=0,5r ...
a=0,5r
|
Gegenüber der gewöhnlichen Epizykloide werden
die Spitzen zu Einbuchtungen.
Die Scheitel und Einbuchtungen werden geglättet und
die Epizykloide artet zum Kreis aus, wenn die Variable a sich Null nähert. |
Verschlungene
Epizykloide (oder Verlängerte E.)
Der Punkt P liegt außerhalb des Kreises
in der Entfernung a von seinem Mittelpunkt.
...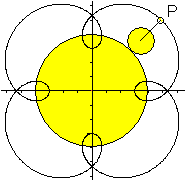 ...
a=2r ...
a=2r
|
Wie der Name besagt, treten bei der verschlungenen Epizykloide
Schlingen auf.
Diese werden umso größer, je größer
die Variable a ist.
Sie überlagern sich schließlich so weit, dass
sie innen m-Ecke aus Bögen bilden.
Das zeigen die folgenden Bildreihen. |
Es folgen Epizykloiden für
m=3 und für verschiedene Parameter a.
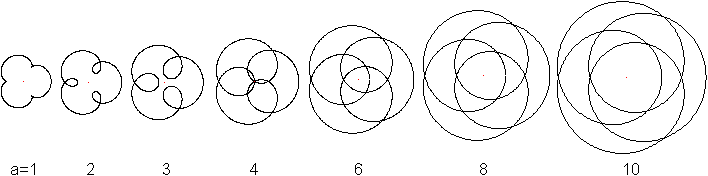
Es folgen Epizykloiden für
m=4 und für verschiedene Parameter a.
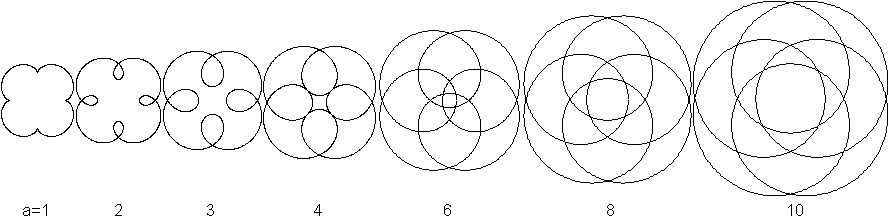
Hypozykloide top
... ... ... |
... ... ... |
Eine Hypozykloide entsteht, wenn sich ein Rollkreis nicht
um,
sondern in einem erzeugenden Kreis bewegt. Dabei verfolgt man den
Weg eines Kreispunktes des abrollenden Kreises. |
Die Hypozykloide wird auch
durch ähnliche Parametergleichungen wie bei Epizykloide beschrieben.
x=(R-r) cos[(r/R)t]+a cos[(1-r/R)t]
y=(R-r) sin[(r/R)t]-a sin[(1-r/R)t]
Die Gleichungen werden auf meiner Webseite Spirograph
hergeleitet und angewandt.
Einige
Beispiele
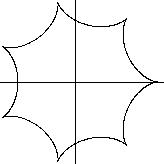
R:r=7:1, a=1
|
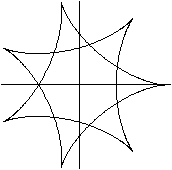
R:r=7:2, a=1
|
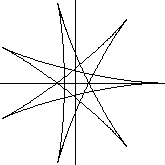
R:r=7:3, a=1
|
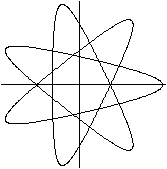
R:r=7:3, a=2
|
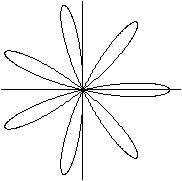
R:r=7:3, a=4
|
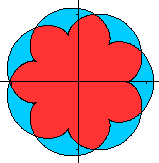
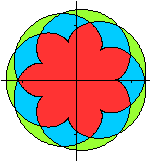
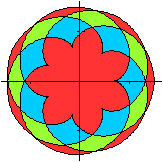
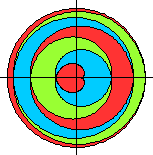
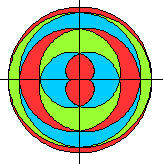
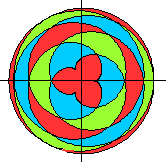
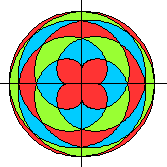
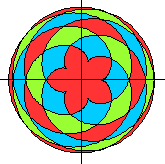
Verfremdung
der Parametergleichungen top
Meist wurden die Figuren noch gedreht, damit die Symmetrieachse
vertikal steht.
Die Bilder von oben jetzt
mit Farbe
Spirograph top
...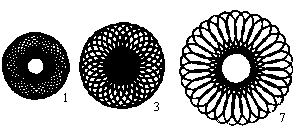 ... ... |
Epi- und Hypozykloide bilden die Grundlage eines weit
verbreiteten Spielzeugs, des Spirographen. |
Epizykloide im
Internet top
Deutsch
Norbert Treitz
Animationen
zu Epi- und Hypotrochoiden
Fachbereich Physik (Universität Innsbruck)
Lissajous-Apparat
Wikipedia
Epizykloide,
Kardioide,
Nephroide,
Zykloide,
Sektorformel
von Leibniz, Spirograph
(Spielzeug)
Englisch
Eric W. Weisstein (MathWorld)
Epicycloid,
Cardioid,
Nephroid,
Ranunculoid,
Tusi
Couple
Famous Curves Index
Epicycloid,
Cardioid,
Nephroid,
Hypocycloid
Gerd Breitenbach
Curves
of planetary motion in geocentric perspective: Epitrochoids
Richard Parris (Freeware-Programme)
winplot
Saltire Software
Area
Enclosed by a General Hypocycloid
Wikipedia
Epicycloid,
Cardioid,
Nephroid,
Epitrochoid,
Hypocycloid,
Spirograph
Xahlee
Epicycloid
and Hypocycloid, Epitrochoid,
Hypotrochoid
Französisch
Robert FERRÉOL, (Mathcurve)
ÉPICYCLOÏDE,
CYCLOÏDE
SPHÉRIQUE, HYPOCYCLOÏDE
Referenzen top
(1) Wilhelm Leupold (u.a.): Analysis für Ingenieur-
und Fachschulen, Frankfurt/M Zürich 1966
(2) Heinz Nickel (u.a.): Algebra und Geometrie
für Ingenieur- und Fachschulen, Frankfurt/M Zürich 1966
(3) W. Gellert (Hrsg.): Kleine Enzyklopädie Mathematik,
Leipzig 1986
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
http://www.mathematische-basteleien.de/
©
2011 Jürgen Köller
top |
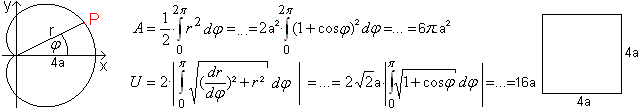
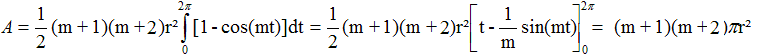 ,wzbw.
,wzbw.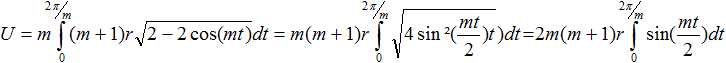
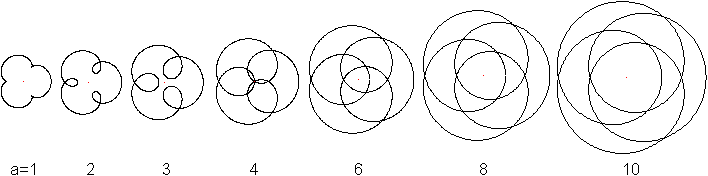
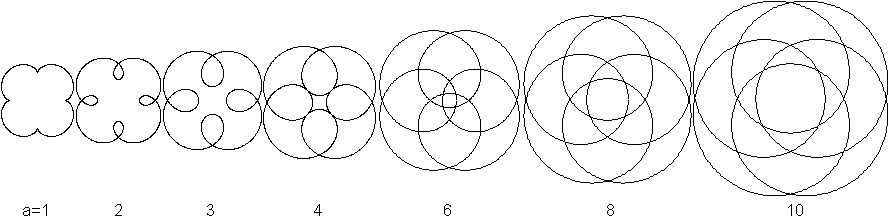
 ...
...

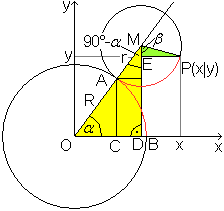

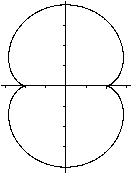
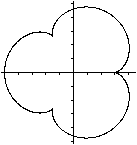

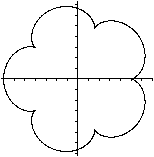
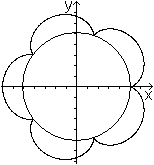 ....
.... ...
...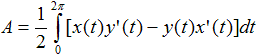
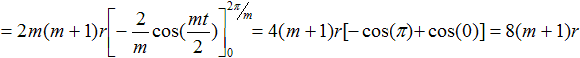 , wzbw.
, wzbw.









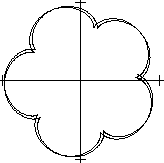




 ...
...
 ...
...
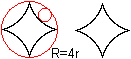 ...
...






 ...
...