|
Was ist eine Hyperbel?
...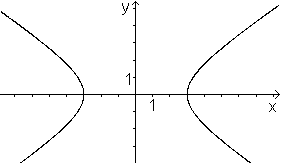 ... ... |
Die Hyperbel ist eine mathematische Kurve.
Man erhält eine einfache Hyperbel als Graph der Relation
mit x²/9-y²/4=1.
Der Definitionsbereich ist Dx={x |x<=-3
/\ x>=3} sowie Dy=|R.
Der Graph besteht aus zwei Ästen.
Er ist symmetrisch bezüglich der Achsen und punktsymmetrisch
bezüglich des Nullpunkts.
Die beiden Punkte, die dem Nullpunkt am nächsten
sind, heißen Scheitelpunkte. |
Hyperbel als Ortslinie
top
Es folgt eine Definition der Hyperbel.
...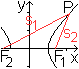 ... ... |
Alle Punkte, deren Differenz der Abstände von zwei
festen Punkten F1 und F2 gleich ist, liegen auf einer
Hyperbel.
Die beiden Punkte heißen Brennpunkte. |
Mit diesem Ansatz gelangt
man zu der Hyperbelgleichung x²/a²-y²/b²=1, die auch
x²/9-y²/4=1 von oben umfasst.
Die Gleichung x²/a²-y²/b²=1 heißt
Mittelpunktsgleichung der Hyperbel. Die Variablen a und b stehen für
positive reelle Zahlen.
Herleitung der Mittelpunktsgleichung
...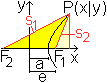 ... ...
|
Es gilt wegen des Satzes von Pythagoras |s1-s2|=|sqrt[y²+(x+e)²]-sqrt[(y²+(x-e)²]|.
Ist y=0, so ist andererseits |s1-s2|=2a.
Somit ist |sqrt[y²+(x+e)²]-sqrt[(y²+(x-e)²]|=2a
die Bestimmungsgleichung der Hyperbel. |
Durch zweimaliges Quadrieren werden die Betragsstriche und
die Wurzelterme entfernt.
Die Gleichung heißt dann
e²x²-a²x²-a²y²-a²e²+(a²)²=0
<=> (e²-a²)x²-a²y²=a²(e²-a²)
Führt man die Variable b über b²=e²-a²
ein, so vereinfacht sich die Gleichung zu b²x²-a²y²=a²b²
oder x²/a²-y²/b²=1, wzbw..
Die Gleichung x²/a²-y²/b²=1
ähnelt der Ellipsengleichung x²/a²+y²/b²=1.
Führt man die imaginäre Zahl i mit i²=-1
ein, stimmt sie mit der Ellipsengleichung überein: x²/a²+y²/(ib)²=1.
So kommt es zu den Bezeichnungen reelle Halbachse für a und imaginäre
Halbachse für b. (Berechnungen zur Ellipse könnten auch formal
auf Hyperbeln übertragen werden. Diese Idee habe ich nicht weiter
verfolgt.)
Diskussion der
Gleichung top
Zahlenbeispiel
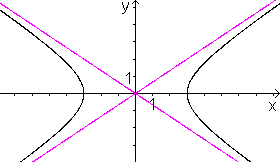
|
Die Hyperbel hat die Gleichung x²/9-y²/4=1
mit a=3 und b=2. |
Definitionsbereich
Die Gleichung x²/a²-y²/b²=1
wird nach y aufgelöst und es ergibt sich y=+(b/a)sqrt(x²-a²)
und y=-(b/a)sqrt(x²-a²).
Die Relation ist nicht definiert für x²<a²
oder |x|<a oder -a< x <a, denn für diese Werte ist der Term
x²-a² unter der Wurzel negativ.
So ergibt sich |Dx=|R\{-a<x<a}.
Asymptoten
Die roten Geraden mit y=(b/a)x und y=-(b/a)x heißen
Asymptoten.
Herleitung der Gleichungen
Für y=+(b/a)sqrt(x²-a²) kann man auch
schreiben y=(b/a)x*sqrt[1-(a²/x²)]. Geht x gegen Unendlich, so
geht y gegen (b/a)x. Die Gleichung y=(b/a)x beschreibt die Asymptote.
Die Gerade und die Hyperbeläste im ersten und dritten Quadranten
nähern sich immer mehr, je größer |x | wird.
Die andere Asymptote ist y=-(b/a)x.
Deutung von b
...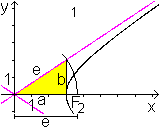 ... ... |
Ist x=a, so gilt für einen Punkt der Asymptote y=b.
Dieser Punkt hat mit dem Scheitelpunkt S(a|0) den x-Wert
gemeinsam.
Die rein formal eingeführte Variable b ist also der
y-Wert der Asymptote in x=a. |
Lage des Brennpunktes
... ... ... |
Die Strecke b bildet mit a ein rechtwinkliges Dreieck.
Die Hypotenuse ist sqrt(a²+b²).
Das aber ist die oben eingeführte Entfernung e des
Brennpunktes vom Nullpunkt. |
Die gleichen Überlegungen gelten für den linken
Brennpunkt.
Alle Formen der Hyperbel
Man erhält alle Formen der Hyperbel, wenn man in
x²/a²-y²/b²=1 für a und b alle positiven reellen
Zahlen einsetzt.
Die Variable a bestimmt die Entfernung der Scheitelpunkte.
Die Variable b bestimmt, wie weit die Hyperbeln auseinander
gebogen werden.
Das veranschaulichen die beiden Bilder.
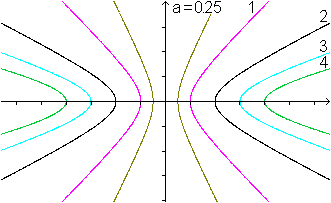
b=1
|

a=1
|
Alle Lagen der Hyperbel
Wird in einem Koordinatensystem das Symmetriezentrum
nach S(x0|y0) verschoben, so führt das zu den
Gleichungen (x-x0)²/a²-(y-y0)²/b²=1.
Drehungen der Hyperbeln werden unten im Kapitel "Hyperbel
als Kegelschnitt" angesprochen.
Gleichseitige
Hyperbel
... ... ... |
Ist a=b=1, so vereinfacht
sich die Hyperbelgleichung x²/a²-y²/b²=1 zu x²-y²=1.
Die Asymptoten werden durch die Gleichungen y=x und y=-x
erfasst. Sie stehen aufeinander senkrecht.
Unten wird dargestellt, dass die Hyperbeln mit a=b auch
Graph einer Funktion werden können. |
Geraden und Hyperbel
top
Offensichtlich schneiden sich Hyperbel
und Gerade in zwei Punkten, in einem Punkt oder gar nicht.
Genauer: Zeichnet man Geraden durch
den Nullpunkt, so gibt es drei Fälle.
...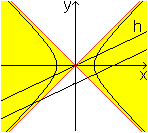 ... ... |
Im ersten Fall sind die Nullpunktsgeraden flacher als
die Asymptoten und liegen im gelben Bereich.
Zeichnet man zu ihnen Parallelen, so schneiden sie die
Hyperbel zweimal.
Die Schnittpunkte liegen auf je einem Ast. |
...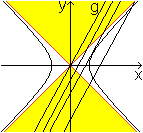 ... ... |
Im zweiten Falle liegen die Nullpunktsgeraden im anderen
Winkelraum, der durch die Asymptoten gebildet wird. Es gibt keinen Schnittpunkt.
Für die Parallelen gibt es drei Möglichkeiten:
Die Gerade schneidet die Hyperbel in zwei Punkten, in
einem Punkt oder gar nicht.
Falls zwei Schnittpunkte auftreten, liegen sie auf einem
Ast.
Interessant ist der Fall genau eines Schnittpunktes.
Dann entstehen Tangenten. |
Dann bleiben noch die beiden
Asymptoten selbst, die als Tangenten der Hyperbel in ihren "unendlich fernen
Punkten" angesehen werden können.
Tangentengleichung
...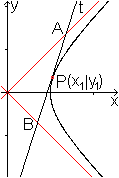 ... ...
|
Lautet die Hyperbelgleichung x²/a²-y²/b²=1
und ist der Berührpunkt P(x1| y1),
so ist die Gleichung der Tangente t
xx1/a²-yy1/b²=1
|
Herleitung
>Die Hyperbelgleichung ist in der Form b²x²-a²y²=a²b²
handlicher.
>Die Ableitung beider Seiten ergibt 2b²x-2a²yy'=0
oder nach y' aufgelöst y'=(b²x)/(a²y).
>Für eine Gerade gilt die Punktrichtungsform (y-y1)/(x-x1)=y'.
>Dabei ist P(x1| y1)
der Berührpunkt und y' die Steigung der Hyperbel im Punkte P.
>Eine Kombination der Gleichungen führt zur Tangentengleichung
(y-y1)/(x-x1)=(b²x)/(a²y) und weiter zu
xx1/a²-yy1/b²=1, wzbw..
Eine Halbierung
...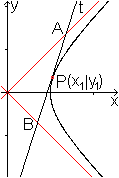 ... ...
|
Die Tangente schneidet die Asymptoten in den Punkten
A und B.
Das Besondere ist, dass der Berührpunkt P den Tangentenabschnitt
AB halbiert. |
Zum Beweis:
>Man bringt die Tangente mit xx1/a²-yy1/b²=1
und die Asymptote mit y=(b/a)x zum Schnitt und erhält xA=a²b/(bx1-ay1).
>Man bringt die Tangente mit xx1/a²-yy1/b²=1
und die zweite Asymptote mit y=-(b/a)x zum Schnitt und erhält
xB=a²b/(bx1+ay1).
>Bildet man (xA+xB)/2, so erhält
man nach längerer Rechnung x1, den x-Wert des Punktes P.
Ein Dreieck
...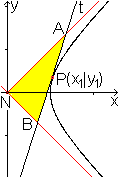 ... ... |
Die Asymptoten und der Tangentenabschnitt bilden ein
Dreieck.
Sein Flächeninhalt AD ist unabhängig
von der Lage des Berührpunktes. Es gilt AD=ab.
Zur Herleitung:
Die x-Werte der Punkte A und B sind xA=a²b/(bx1-ay1)
und xB=a²b/(bx1+ay1).
Dann sind nach y=(b/a)x die y-Werte yA=ab²/(bx1-ay1)
und yB=ab²/(bx1+ay1).
Aus den Koordinaten des Dreiecks NBA ergibt sich AD=(1/2)(xByA-yBxA)=ab. |
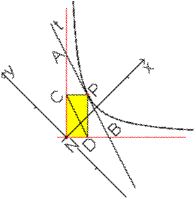
Ein
Parallelogramm
...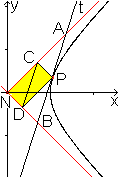 ... ... |
Man zeichnet in das Dreieck NBA die drei Mittelparallelen.
Dann entsteht das Parallelogramm NDPC.
Das Parallelogramm hat den Flächeninhalt ab/2. Es
ist halb so groß wie der Flächeninhalt des Dreiecks NBA.
Der Flächeninhalt hängt somit nicht von der
Lage des Berührpunktes P ab.
In der Zeichnung ist das Parallelogramm nur deshalb ein
Rechteck, weil die Hyperbel gleichseitig ist und die Asymptoten orthogonal. |
Zwei
gleiche Strecken
...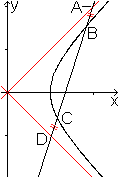 ... ... |
Wenn eine Gerade die Hyperbel in den Punkten C und B
schneidet und die Asymptoten in den Punkten D und A, so gilt DC=BA.
Zum Beweis:
Die Sekante ist durch y=mx+n und die Hyperbel durch x²/a²-y²/b²=1
beschrieben.
Man berechnet die Mittelpunkte der Strecken AD und CB
und erhält in beiden Fällen nach längerer Rechnung
xm=a²n/(b²-a²m²) und
ym=b²n/(b²-a²m²).
|
Quelle (2) Aufgabe 988
Hyperbel
als Bild einer Funktion top
Entstehung
Dreht man (z.B. mit Irfan) das Bild einer Hyperbel mit
senkrecht aufeinander stehenden Asymptoten um -45°, so werden die Asymptoten
zu Achsen eines neuen Koordinatensystems und die Hyperbel wird zum Graph
einer Funktion.
Einfache
Hyperbel
Die einfachste Hyperbelgleichung dieser Art ist f(x)=1/x.

|
Diese Hyperbel kann angesehen werden
>als Graph der Stammbrüche 1, 1/2, 1/3, 1/4,...
>Zur Veranschaulichung der Nullfolge <1/n> (rot).
>Als Ort von Ecken der Rechtecke mit dem Flächeninhalt
1. |
Antiproportionale
Größen
...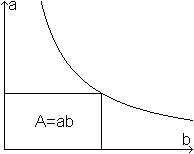 ... ... |
Die Hyperbel veranschaulicht Dreisatzaufgaben vom Typ
"je größer, desto kleiner".
Beispiel:
Die Länge a und die Breite b eines Rechtecks bei
konstantem Flächeninhalt A, a=A/b
"Je größer die eine Seite des Rechtecks ist,
desto kleiner wird die andere."
Länge und Breite sind produktgleich oder
umgekehrt
proportional oder antiproportional.
Aus y=1/x wird die Zuordnungsgleichung a=A/b.
|
Abgeleitete
Funktionen
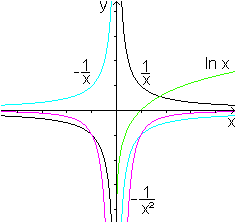
|
Die Funktion mt f(x)=1/x führt zu folgenden drei
neuen Funktionen.
>f(-x)=-1/x (Spiegelfunktion)
>f '(x)=-1/x² (Erste Ableitung)
>F(x)=ln(x) (Stammfunktion)
Die Umkehrfunktion von f(x)=1/x ist die Funktion selbst.
|
Zwei
uneigentliche Integrale
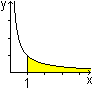
|

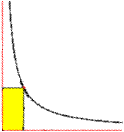
|
Die Fläche unter der Hyperbel rechts von x=1 ist
unendlich groß. |
... ... ... |
Lässt man aber die Hyperbel um die x-Achse rotieren,
so ist merkwürdigerweise das Volumen des ins Unendliche reichenden
Rotationskörpers endlich und gleich pi. |
Verallgemeinerungen
...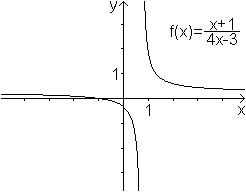 ... ... |
Den Funktionsterm 1/x kann man verallgemeinern zu der
"gebrochenen linearen Funktion" f(x)=(a1x+b1)/(a2x+b2)
mit D=a1b2-a2b1 ungleich Null
und a2 ungleich Null.
Näheres findet man im Bronstein (3) Seite 73f. |
...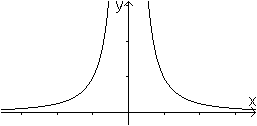 ... ... |
Bei meinen Recherchen stellte ich fest, dass die Graphen
gebrochener rationaler nicht-linearer Funktionen nicht als Hyperbeln
bezeichnet werden, obwohl sie wie die Hyperbeln oft asymptotisches Verhalten
zeigen.
Für den Graphen der einfachsten Funktion dieser Art,
nämlich f(x)=1/x² , ist allerdings der Name Hyperbel gebräuchlich.
Dieser ist auch monoton und hat Asymptoten. |
Hyperbel zeichnen
top
In älteren Büchern betont
man Anleitungen, wie man eine Hyperbel zeichnen kann. [(1) Seite 165]
Gegeben sind jeweils die Brennpunkte F1 und
F2 und die Entfernung der Scheitelpunkte 2a.
Punktweise Konstruktion
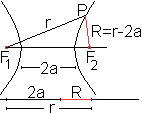
|
>Zeichne einen Kreis mit einem Radius r>F1F2.
>Bestimme die Strecke R=r-2a.
>Zeichne einen Kreis um F1 mit dem Radiur R.
Der Schnittpunkt P ist ein Punkt der Hyperbel. |
Fadenkonstruktion
...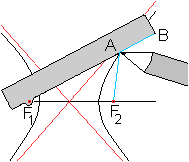 ... ... |
> Befestige ein Lineal drehbar im Brennpunkt F1.
>Befestige das eine Ende eines Fadens in Brennpunkt F2,
das andere am Ende des Lineals.
>Wähle die Fadenlänge s so, dass sie gleich
der Differenz aus der Länge des Lineals F1B=t und der gegebenen
Strecke 2a ist. (D.h. t-s=2a).
>Eine Hyperbel ergibt sich, wenn man das Lineal um F1
dreht und dabei einen Bleistift gegen das Lineal und auf das Papier drückt
und darauf achtet, dass der Faden gespannt bleibt. |
Begründung
Es gilt F2A+AB=s und F1A+AB=t.
Daraus folgt mit t-s=2a durch Differenzenbildung F1A-F2A=2a,
wzbw..
Hyperbel als
Kegelschnitt
top
Kegelschnitte
...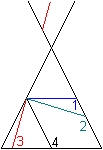 ... ... |
Legt man durch einen geraden Doppelkegel ebene Schnittflächen,
so entstehen im wesentlichen vier Arten von Linien.
1 Ein Schnitt parallel zum Grundkreis führt zum
Kreis.
2 Eine Schnittebene, die den zweiten Einzelkegel nicht
trifft, erzeugt eine Ellipse.
3 Eine Schnittebene, die beide Einzelkegel erreicht,
erzeugt eine Hyperbel.
4 Ein Schnitt parallel zu einer Mantellinie ergibt eine
Parabel.
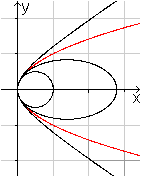
Rechts die vier Linien in der bekannten Darstellung in
einem Koordinatensystem. |
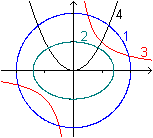 |
Scheitelgleichungen
der Kegelschnitte
|
Die Scheitelgleichung für Kegelschnitte lautet:
y²=2px+(epsilon²-1)x²
Es ergeben sich
> der Kreis für epsilon = 0
> die Ellipse für epsilon = 0,8
> die Parabel für epsilon = 1
> die Hyperbel für epsilon = 1,2. |
Quadratische
Gleichung mit zwei Variablen
...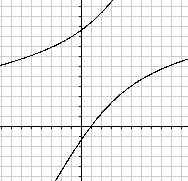 ... ...
|
Alle Kegelschnitte erfasst man auch durch die Gleichung
Ax²+Bxy+Cy²+Dx+Ey+F=0.
Eine Hyperbel liegt vor, wenn im wesentlichen 4AC-B²<0
ist (3).
Die nebenstehende Hyperbel ist der Graph der Relation
4x²+24xy+11y²+144x-92y-140=0.
Es ist 4AC-B²=4*4*11-24²=-400<0
Offensichtlich bewirkt der Term mit xy eine Neigung der
Symmetrieachsen.
Quelle: (2) Aufgabe 991e |
Hyperbel im Internet
top
Deutsch
Wikipedia
Hyperbel
(Mathematik), Hyperboloid,
Dreisatz,
Proportional,
Antiproportionalität
Englisch
Gary S. Stoudt (Convergence MAA)
Can
You Really Derive Conic Formulae from a Cone?
Eric W. Weisstein (MathWorld)
Hyperbola,
Confocal
Hyperbolas, Confocal
Conics, Rectangular
Hyperbola
Ferner: Stammler
Hyperbola, Feuerbach
Hyperbola, Yff
Hyperbola, Jerabek
Hyperbola, Hyperbola
Inverse Curve, Hyperbola
Pedal Curve
Xah Lee
Hyperbola
Wikipedia
Hyperbola,
Hyperbolic
sector,
Hyperbolic
angle,
Hyperbolic
function,
Hyperboloid,
Rule
of three (mathematics), Proportionality
(mathematics)
Französisch
Robert FERRÉOL (mathcurve)
Hyperbole
Referenzen top
(1) Otto Zoll: Mathematisches Lehr- und Arbeitsbuch für
höhere Lehranstalten, Oberstufe, Braunschweig 1940
(2) Autorengemeinschaft: Algebra und Geometrie
für Ingenieure, Frankfurt/M Zürich 1966 [ISBN 978-3-87144-107-3]
(3) I.N.Bronstein, K.A.Semendjajew: Taschenbuch der Mathematik,
Leipzig 1987
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2007 Jürgen Köller
top |
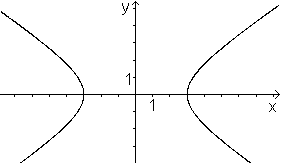 ...
... ...
...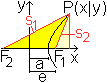 ...
...
 ...
...

 ...
... ...
... ...
...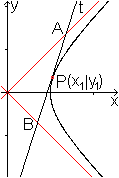 ...
...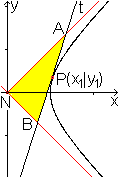 ...
... ...
... ...
...

 ...
...
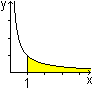

 ...
...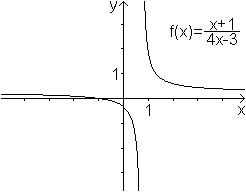 ...
... ...
...
 ...
... ...
...

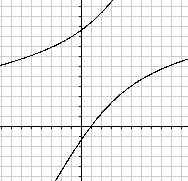 ...
...