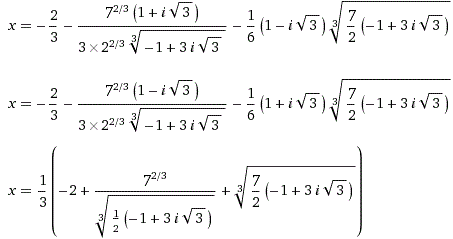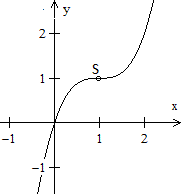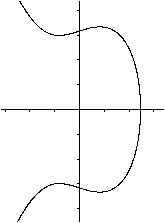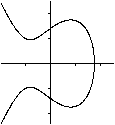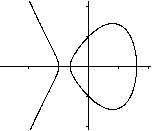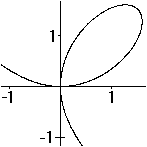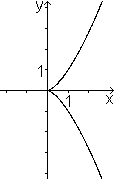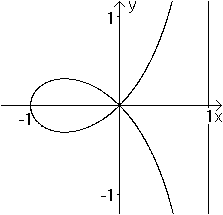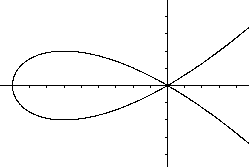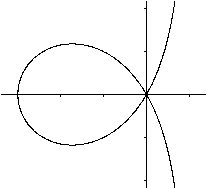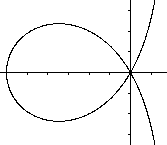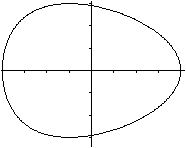|
Was ist eine kubische Parabel?
... ... |
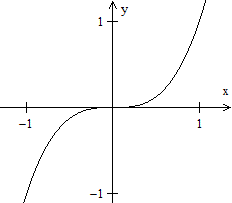Die kubische Parabel ist der Graph der Funktion mit f(x)
= x³.
In Analogie zur (quadratischen) Normalparabel mit q(x)
= x² könnte man die Kurve genauer kubische Normalparabel nennen. |
... ... |
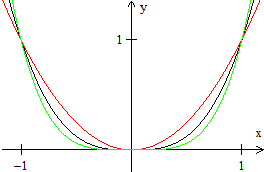Die kubische Normalparabel reiht sich zwischen quadratischer
Normalparabel und dem Graphen zu y=x4
ein.
Die Funktionsterme sind x2,
|x|3 und x4. |
... ... |
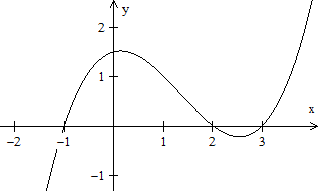Die kubische Parabel im weiteren Sinne ist der Graph
der ganzrationalen Funktion mit
f(x) = ax³+bx²+cx+d.
Man fordert a ungleich 0, damit die dritte Potenz nicht wegfällt.
Die Vorzahlen a, b, c und d stehen für reelle Zahlen.
Der größtmögliche Definitionsbereich
ist D=|R, der Wertebereich ist dann auch W=|R.
Als ein Beispiel steht links ein Graph mit dem Funktionsterm
f(x) = (1/4)(x+1)(x-2)(x-3) = (1/4)(x³-4x²+x+6)
= (1/4)x³-x²+(1/4)x+3/2.
|
Diskussion
der Beispielfunktion top
Für eine Kurvendiskussion benötigt man die
ersten drei Ableitungen.
f(x) = (1/4)x³-x²+(1/4)x+3/2
f '(x) = (3/4)x²-2x+1/4
f ''(x) = (3/2)x-2
f '''(x) = 3/2
Die Stammfunktion ist F(x) = (1/16)x4-(1/3)x3+(1/8)x2+(3/2)x+C.
Es gilt F'(x)=f(x).
Nullstellen
Es gilt f(x) = 0 oder (1/4)x³-x²+(1/4)x+3/2
= 0.
Es ist kein großes Problem, die Gleichung zu lösen,
da der Funktionsterm ursprünglich in der Produktform f(x) = (1/4)(x+1)(x-2)(x-3)
gegeben war. Die Nullstellen sind x1 = -1, x2
= 2 und x3 = 3.
Der y-Achsen-Abschnitt ist f(0) = 3/2.
Extremstellen
Es gilt f'(x)=0.
(3/4)x²-2x+1/4=0 führt zu x²-8/3x+1/3
= 0 oder x4 = 4/3+(1/3)sqrt(13) und x5
= 4/3-(1/3)sqrt(13).
Angenäherte Zahlen sind x4 = 2,535 und
x5 = 0,131.
Es gilt f ''(x4) = f ''(2,535) = 1,5*2,535
-2 > 0 und f ''(x5) = f ''(0,131) = 1,5*0,131 -2 <0.
Damit ist x4 eine Minimalstelle und x5
ist eine Maximalstelle.
Wendestelle
Es gilt f ''(x) =0.
(3/2)x-2 = 0 führt zu x6 = 4/3.
Da f '''(x) = 3/2 , also ungleich 0, ist, ist x6
= 4/3 eine Wendestelle.
Verhalten
"im Unendlichen"
Geht x gegen Unendlich, so geht auch f(x) gegen Unendlich.
Geht x gegen - Unendlich, so geht auch f(x) gegen - Unendlich.
Eine
Flächenberechnung
... ... |
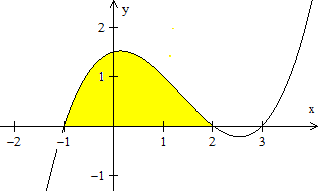Für die gelbe Fläche gilt
|
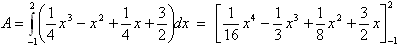
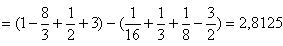
Graph der Funktion
|
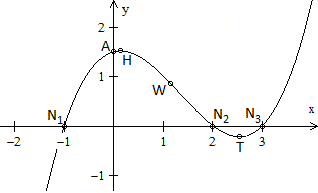
Die Graphen der Funktion, ihrer
Ableitungen und der Stammfunktion für C=0
|
f(x)
f '(x)
f ''(x)
F(x)
............................ |
Für die folgenden Überlegungen benötigt
man die Ableitungen der allgemeinen kubischen Funktion.
f(x) = ax³+bx²+cx+d (a nicht
gleich 0).
f '(x) = 3ax²+2bx+c
f ''(x) = 6ax+2b
f '''(x) = 6a
Punktsymmetrie
der kubischen Parabel top
Quadratische Parabel
... ... |
Die quadratische Parabel ist achsensymmetrisch bezüglich
der Vertikalen durch den Scheitelpunkt. |
Kubische
Parabel
In Analogie gilt die Aussage: Die kubische Parabel ist
punktsymmetrisch bezüglich des Wendepunktes.
Dazu folgen Überlegungen in vier Schritten.
1
... ... |
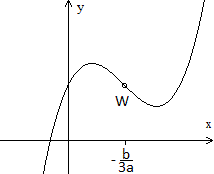Für den Wendepunkt muss gelten: f ''(x) = 0 und
f '''(x) ungleich 0.
Das führt zu 6ax+2b = 0 oder x=-b/(3a). Die zweite
Bedingung ist erfüllt.
Ergebnis: Die Wendestelle liegt bei x= -b/(3a). |
2
Es gilt der Satz: Der Graph einer Funktion ist punktsymmetrisch
bezüglich des Nullpunkts, wenn für alle x gilt f(x) = -f(-x).
... ... |
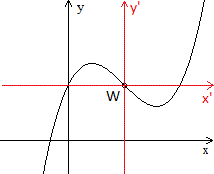Um diesen Satz anwenden zu können, wird das Koordinatensystem
so verschoben, dass der Wendepunkt Nullpunkt eines neuen x'-y'-Koordinatensystems
wird.
Dazu setzt man x = [x'-b/(3a)] in den allgemeinen Funktionsterm
f(x) = ax³+bx²+cx+d ein
.
Wie sich dann gleich zeigen wird, fällt dann der quadratische
Term weg. |
3
y = a[x'-b/(3a)]³+b[x'-b/(3a)]²+c[x'-b/(3a)]+d
= a{x'³-3x'²[b/(3a)]+3x'[b/(3a)]²-[b/(3a)]³}+b{x'²-2[b/(3a)]x'+[b/(3a)]²}+cx'-c[b/(3a)]+d
= ax'³-bx'²+(3ab²)/(9a²)x²-b³/(27a³)+bx'²-[(2b²)/(3a)]x'+b²/(9a²)+cx'-(bc)/(3a)+d
= ax'³+[(3b²)/(9a)-(2b²)/(3a)+c]x'+[-b³/(27a²)+b³/(9a²)-(bc)/(3a)+d]
= ax'³+[(3ac-b²)/(3a)]x'+[(2b³-9abc+27a²d)/(27a²)]
Der freie Term (2b³-9abc+27a²d)/(27a²)
ist gerade f [-b/(3a)], also die Ordinate des Wendepunktes im x-y-Koordinatensystem.
4
Damit hat die Parabel im x'-y'-Koordinatensystem die
Darstellung y' = ax'³+[(3ac-b²)/(3a)]x'.
Da nur die ungeraden Exponenten 1 und 3 im Funktionsterm
vorkommen, gilt f(x) = -f(-x). Der Graph ist somit punktsymmetrisch bzgl.
des neuen Nullpunkts und der Graph der gegebenen Funktion punktsymmetrisch
bzgl. des Wendepunkts.
Nullstellen
kubischer Parabeln top
Lösen durch Probieren
Das soll am Beispiel f(x)=x³-x²-3x+3 erklärt
werden.
Man berechnet f(x) für verschiedene Zahlen x und
hofft, dass f(x)=0 wird. Gesteuert wird das durch die Aussage, dass x ein
Teiler von 3 sein muss. Das sind hier die Zahlen -3, -1, 1, 3.
Setzt man z.B. x=1, so gilt f(1)=1-1-3+3 = 0. Also ist
x=1 eine Nullstelle.
Durch die Polynomdivision (x³-x²-3x+3):(x-1)
gelangt man zu x²-3 und zur quadratischen Gleichung x²-3=0.
Die Lösungen sind also x1=1, x2=sqrt(3)
und x3=-sqrt(3).
Diese Methode gelingt nur, wenn es mindestens eine ganzzahlige
Lösung gibt.
Vorbemerkung
Es geht darum, die allgemeine Gleichung ax³+bx²+cx+d
= 0 zu lösen.
An dieser Stelle sollten eigentlich die Herleitung der
Lösungsformeln von Cardano und die Überlegungen zum "Casus irreducilus"
stehen. Das sind nämlich die Standardlösungen kubischer Gleichungen.
Bei meinen Recherchen im Internet stellte ich fest, dass ich mir das schenken
kann ;-). Im Internet findet man eine Reihe ausführlicher Herleitungen.
Ich nenne
> den Aufsatz von Max Krause (URL unten).
> den Aufsatz bei Matroids Matheplanet (URL unten).
Lösung der quadratischen
Gleichung
Ein besseres Verständnis für die Bestimmung
der Nullstellen erhält man, wenn man sich die Lösung der allgemeinen
quadratischen Gleichung ax²+bx+c=0 vergegenwärtigt und auf die
kubische Gleichung überträgt.
1.Schritt:
Man dividiert beide Seiten der Gleichung durch die Vorzahl
von x² und erhält die Normalform x²+px+q = 0 mit p=b/a und
q=c/a.
2.Schritt:
Nach der p-q-Formel ist x1 = -p/2+sqrt(p²/4-q)
und x2 = -p/2-sqrt(p²/4-q). Dabei ist D = p²/4-q =
(p²-4q)/4 = (b²-4ac)/(4a²) die Diskriminante.
Man bezeichnet oft auch den einfacheren Term im Zähler,
nämlich p²-4q oder b²-4ac als Diskriminante.
... ... |
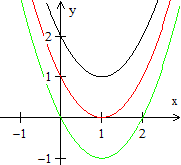Die Rechnung muss man so interpretieren.
Es gibt für die quadratische Funktion drei Fälle
bezüglich der Nullstellen.
1. Fall: D=0
Es gibt nur eine Nullstelle. |
2. Fall: D>0
Es gibt zwei Nullstellen. |
3. Fall: D<0
Es gibt keine Nullstelle. |
Beispiele:
| Für f(x)=(x-1)²
ist D=0. |
Für f(x)=(x-1)²-1
ist D=1>0. |
Für f(x)=(x-1)²+1 ist D=-1<0. |
|
Lösung
der kubischen Gleichung
... ... |
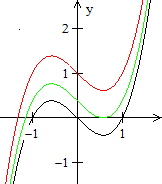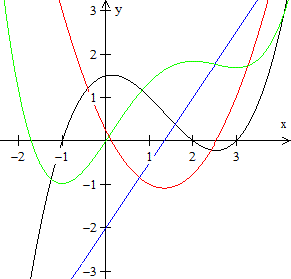
Stellt man kubische Funktionen graphisch dar, so ergeben
sich auch drei Fälle.
1. Fall: Es gibt drei Nullstellen (schwarze Kurve).
2. Fall: Es gibt zwei Nullstellen (grüne Kurve).
Dabei ist eine Stelle eine doppelte Nullstelle.
3. Fall: Es gibt eine Nullstelle (rote Kurve).
Die Funktionsterme sind übrigens x(x+1)(x-1), x(x+1)(x-1)+1
und x(x+1)(x-1)+(2/9)sqrt(3). |
... ... |
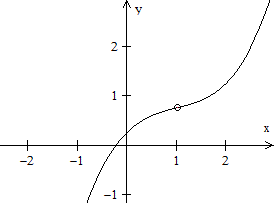Man sollte die Graphen ohne Extremwerte nicht vergessen,
z.B. den zu f(x) = (1/4)(x³-3x²+4x+2).
Er ist monoton steigend.
Verschiebt man ihn längs der y-Achse, so gibt es
immer genau einen Schnittpunkt mit der x-Achse.
Wie im 3.Fall oben gibt es genau eine Nullstelle. |
Wie bei der quadratischen
Gleichung gibt es eine Diskriminante, die es erlaubt, die drei Fälle
zu unterscheiden.
Die Diskriminante zur kubischen Gleichung ax³+bx²+cx+d
= 0 ist im wesentlichen D = q²+4p³ mit p = 3ac-b² und q
= 2b³-9abc+27a²d.
Fall 1: Ist D>0, so gibt es eine reelle Lösung.
Fall 2: Ist D=0, so gibt es zwei reelle Lösungen,
wobei eine Lösung eine doppelte Nullstelle ist.
Fall 3: Ist D<0, so gibt es drei reelle Lösungen.
Es ist heute kein Problem,
kubische Gleichungen angenähert durch Dezimalzahlen zu lösen.
Es gibt im Internet zahlreiche Applets unter dem Namen "cubic equation
solver". Ich habe den von wolframalpha (URL unten) für die folgenden
drei der vier typischen Funktionen verwendet.
Beispiel
1: Eine reelle Nullstelle
Die Funktion sei f mit f(x)=(1/8)(x³-x²+x+1).
Die Diskriminante zu x³-x²+x+1 = 0 ist D =
q²+4p³ = (2b³-9ab+27a²d)²+4(3ac-b²)³
= 34²-4*2³ >0.
Da D>0 ist, gibt es nur eine reelle Nullstelle.
... ... |
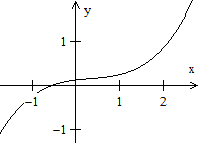Statt der Gleichung (1/8)(x³-x²+x+1) = 0 kann
man auch x³-x²+x+1 = 0 lösen.
Die Berechnung überlasse ich besser dem "cubic equation
solver".
| Exakt: |
 |
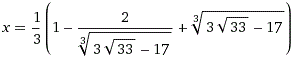Gerundet x = - 0,54369 |
Auch wenn man den Graphen
in y-Richtung verschiebt, bleibt es bei einer Nullstelle. Das gilt nicht
für die nächsten Beispiele.
Beispiel
2: Eine reelle Nullstelle
Die Funktion sei f mit f(x)=x³+2x²+x-1.
Die Diskriminante ist D = q²+4p³ = (2b³-9abc+27a²d)²+4(3ac-b²)³
= (-29)²+4(-1)³ >0.
Da D>0 ist, gibt es nur eine reelle Nullstelle.
... ... |
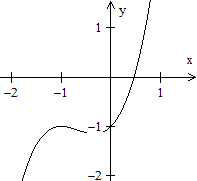Die Berechnung überlasse ich wieder besser dem "cubic
equation solver".
Angenähert: 0,46557
| Exakt: |
 |
|
|
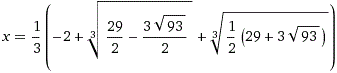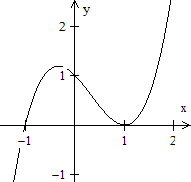
Beispiel 3:
Zwei
reelle Nullstellen
Die Funktion sei f mit f(x)=x³-x²-x+1.
... ... |
Die Diskriminante ist D = q²+4p³ = (2b³-9abc+27a²d)²+4(3ac-b²)³
= 16²+4*(-4)³ = 0.
Da D=0 ist, gibt es zwei reelle Nullstellen.
Es gilt f(x)=x³-x²-x+1 =(x-1)²(x+1).
Die Nullstellen sind also x1=-1 und x2=1. |
Beispiel
4: Drei reelle Nullstellen
Die Funktion sei f mit f(x)=x³+2x²-x-1.
Die
Diskriminante ist D = q²+4p³ = (2b³-9abc+27a²d)²+4(3ac-b²)³
= 7²+4(-7)³ <0.
Da D<0 ist, gibt es drei reelle Nullstellen. Angenähert
sind das x1=-2,2470, x2=-0,55496, x3=0,80194.
... ... |
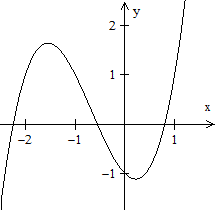Der "cubic equation solver" gibt auch die folgenden
genauen Lösungen an:
 |
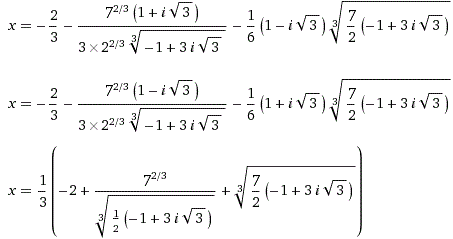Es fällt auf, dass die Terme noch die imaginäre
Zahl i=sqrt(-1) enthalten. Merkwürdigerweise bedeuten die Terme aber
reelle Zahlen.
Um sie zu bestimmen, müsste man noch cos(phi)=(-q)/[2*sqrt(-p³)]
einführen (siehe z.B. Ende des Aufsatzes von Alf Krause, URL unten).
Das leistet das Programm "cubic equation solver" nicht.
Extremstellen
kubischer Parabeln top
Für eine Extremstelle muss gelten: f '(x) = 0 und
f ''(x) ungleich 0.
f '(x) = 0 führt zu 3ax²+2bx+c =0 oder
x²+(2b/3a)x+c/(3a)=0.
Die Lösungen sind x1 = -b/(3a)+sqrt[b²/(9a²)-c/(3a)]
und x2 = -b/(3a)-sqrt[b²/(9a²)-c/(3a)].
Umgeformt x1 = [1/(3a)][-b+sqrt(b²-3ac)]
und x2 = (1/(3a)[-b-sqrt(b²-3ac)].
Für die zweite Ableitung gilt f ''(x1)
= 6ax1+2b = -2b+2sqrt(b²-3ac)+2b = 2sqrt(b²-3ac)>0
und f ''(x2) = -2sqrt(b²-3ac)<0.
Ergebnisse:
> Die beiden Nullstellen sind reell, wenn die Diskriminante
D = b²-3ac>0 ist.
> An der Stelle x1 = (1/(3a)[-b+sqrt(b²-3ac)]
liegt ein Minimum.
> An der Stelle x2 = (1/(3a)[-b-sqrt(b²-3ac)]
liegt ein Maximum.
Zwei typische Beispiele
| f(x) = (1/4)x³-x²-(1/4)x+3/2
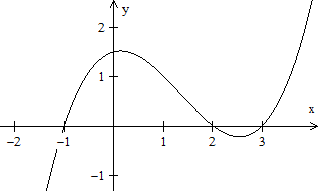x1 = 4/3+(1/3)sqrt(13) und x2
= 4/3-(1/3)sqrt(13) |
f(x) = -(1/4)x³+x²+(1/4)x-3/2
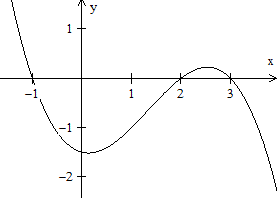x1 = 4/3+(1/3)sqrt(13) und x2
= 4/3-(1/3)sqrt(13) |
Wendestelle
kubischer Parabeln top
Oben wurde schon nachgewiesen, dass der Wendepunkt Symmetriezentrum
der punktsymmetrischen kubischen Parabel ist.
Für eine Wendestelle muss gelten: f ''(x) = 0 und
f '''(x) ungleich 0.
f ''(x) = 0 führt zu 6ax+2b = 0 oder zu der Lösung
x = -b/(3a).
Da die dritte Ableitung f '''(x) = 6a für alle x-Werte
ungleich 0 ist, liegt wirklich eine Wendestelle vor.
Die Steigung im Wendepunkt ist f '(x) = 3ax²+2bx+c
= (3ab²)/(9a²) -(2b²)/(3a)+c = c-b²/3a = (3ac-b²)/(3a).
Sattelpunkt
Ein besonderer Fall liegt vor, wenn die Steigung f '(x)
= 0 ist. Das heißt 3ac-b² = 0 oder D=0.
Dann heißt der Wendepunkt mit waagerechte Tangente
Sattelpunkt.
Ergebnisse:
> An der Stelle x = -b/(3a) liegt die einzige Wendestelle.
> Ein Sattelpunkt liegt vor, wenn 3ac-b² = 0 ist.
Zwei
typische Beispiele
| f(x) = (1/4)(x³-3x²+4x+1)
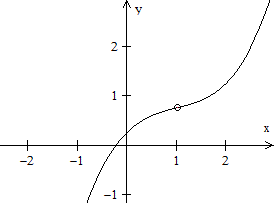Wendestelle in x= 1 mit der Steigung 1/4 |
f(x)=(x-1)³-1 = x³-3x²+3x.
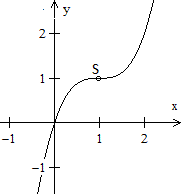Sattelpunkt in x=1 |
Funktion suchen top
Eine Anwendung linearer Gleichungssysteme ist das Suchen
von Funktionen dritten Grades. Man gibt Eigenschaften einer kubischen Parabel
vor und soll dann ihre Funktionsgleichung finden. Dazu ein Beispiel.
Gegeben sei eine kubische Parabel mit der Nullstelle
x1=-1. Eine zweite Nullstelle sei x=1 mit der Steigung 0. Sie
schneide die y-Achse in y=1.
Lösung
Der Ansatz ist f(x) = ax³+bx²+cx+d. Dann ist
f '(x) = 3ax²+2bx+c.
Es gilt
f(1) = 0 oder a+b+c+d =0
f '(1) =0 oder 3a+2b+c = 0
f(-1) = 0 oder -a+b-c+d = 0
f(0) = 1 oder d=1.
Das führt zu den drei Gleichungen
(I) a+b+c=-1,
(II) 3a+2b+c = 0,
(III) -a+b-c = -1. |
(II)+(III) ergibt 2a+3b = -1.
(I)-(II) ergibt -2a-b = -1. |
Dann ist b=-1, a=1 und weiter c = -3a-2b = -1. |
Ergebnis: Die Funktionsgleichung ist f(x) = x³-x²-x+1.
Normalform
der kubischen Funktion top
Oben wurde gezeigt, dass die kubische Funktionsgleichung
durch eine Koordinatenverschiebung auf die Form y' = ax'³+[(3ac-b²)/(3a)]x'
gebracht werden kann. Normiert man sie noch mit a=1, so erhält man
die einfache Form f(x) = x³+kx. Das ist die Normalform.
An ihr lassen sich einfacher wie oben Eigenschaften der
kubischen Parabel ablesen.
Z.B. folgt aus der ersten Ableitung f '(x) = 3x²+k,
dass eine kubische Parabel zwei Extrempunkte hat, wenn k=-1 ist. Es gibt
keinen Extrempunkt, wenn k=1 ist.
Kurven
dritten Grades auf meiner Homepage top
Auf verschieden Seiten meiner Homepage findet man Kurven
dritten Grades. Sie werden durch die folgende Gleichung beschrieben.
f(x) = a1y³+a2y²x+a3yx²+a4x³+a5y²+a6yx+a7x²+a8y+a9x+a10
strophoide.htm
Gerade Strophoide
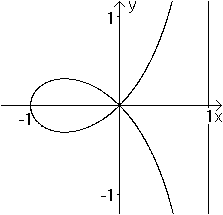
y²(1-x)-x²(1+x)=0 |
Tschirnhausen-Kubik
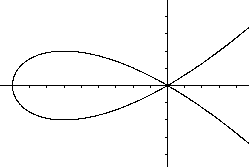
27ay²=x²(9a-x) mit a=-1 |
Konchoide von de Sluze
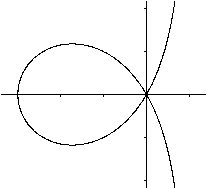
(x-1)(x²+y²)-a²x²=0 mit a=1 |
Trisectrix des Maclaurin
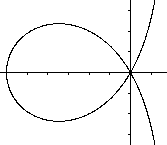
2x(x²+y²)+4(3x²-y²) |
glockenkurve.htm
Versiera der Maria Agnesi
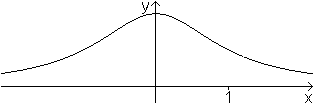
y=1/(x²+1)
|
Chonchoide von de Sluze
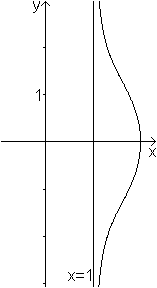
(x-1)(x²+y²)=x² |
Fermat-Kubik
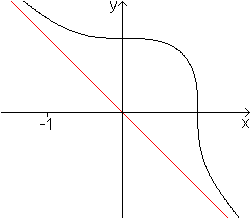
x³+y³=1 |
Ausgangsfunktion: f(x) = x(x+1)(x-1)
|
Ausgangsfunktion: f(x) = (1/4)x(x²+1)
|
Referenzentop
(1) W.Gellert (Herausgeber u.a.): Kleine Enzyklopädie
Mathematik, Leipzig 1986
(2) I.N.Bronstein, K.A.Semendjajew: Taschenbuch der Mathematik,
Leipzig 1987
Kubische
Parabeln im Internet top
Deutsch
Arndt Brünner
Nullstellen
(Lösungen) von Polynomen bestimmen (Applet)
Jörg Meyer
DIE
RÄUMLICHE PARABEL MIT DEM ALLGEMEINEN PUNKT (t,t²,t³)
Jutta Gut
Spitzen,
Schlingen, Ostereier - Kurven dritten Grades
Martin_Infinite (Matroids Matheplanet)
Die
kubische Gleichung
Wikipedia
Kubische
Gleichung, Polynom,
Ganzrationale
Funktion, Potenzfunktion,
Elliptische
Kurve
Englisch
Math Open Reference
Cubic
Function Explorer (Graphing tool)
Richard Parris (Freeware-Programm WINPLOT)
Die offizielle Webseite ist geschlossen. Download des
deutschen Programms z.B. bei heise
Wikipedia
Cubic
function, Polynomial,
Polynomial,
Power
function,
Elliptic
curve,
Cubic
plane curve,
Tschirnhausen
cubic, Twisted
cubic
wolframalpha.com
Cubic
equation solver
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2014 Jürgen Köller
top |
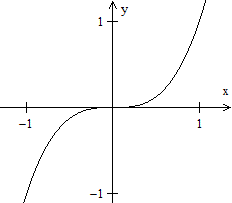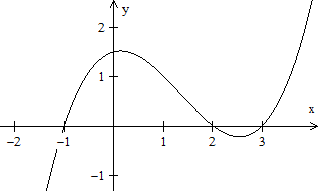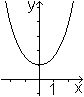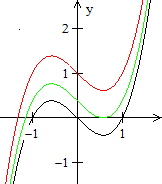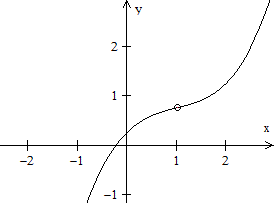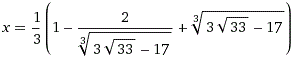
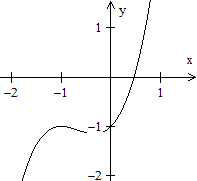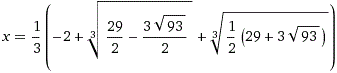
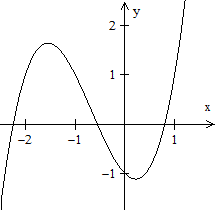