|
Was ist der Bascetta-Stern?
... ... ... |
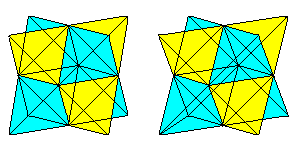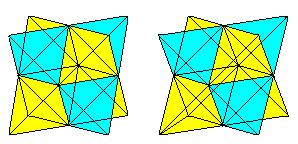
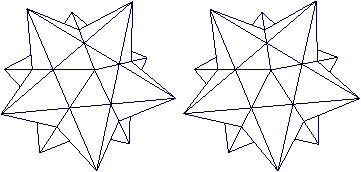
Der Bascetta-Stern ist ein dreidimensionaler Stern, der
aus 30 Modulen zusammengesteckt wird.
Die Module werden aus Quadraten gefaltet.
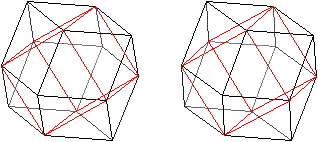
Mathematisch gesehen ist er ein Ikosaeder, auf dessen
Seitenflächen 20 Dreieckspyramiden stehen. |
Der Name geht auf den Erfinder des Moduls und des Sterns,
den Italiener Paolo Bascetta, zurück.
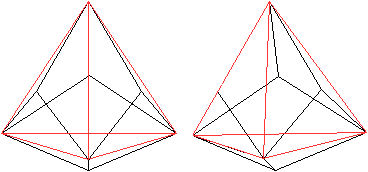
Vergleich
mit dem Großen Sterndodekaeder top
Das Große
Sterndodekaeder hat den gleichen Aufbau. Es ist auch ein Ikosaeder
mit geraden Dreieckspyramiden als Krönung, allerdings sind die Zacken
spitzer.
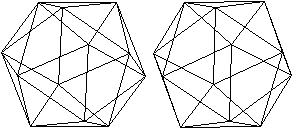
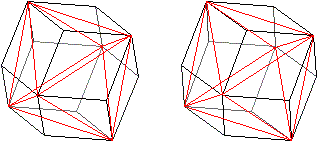
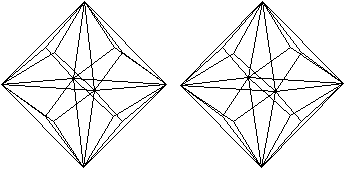
Ikosaeder
|
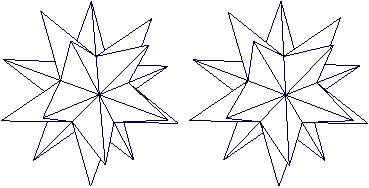
|
...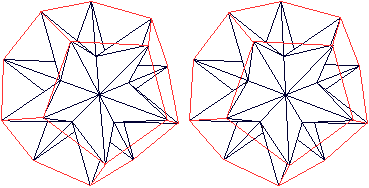 ... ... |
Die Bezeichnung Dodekaeder erklärt sich dadurch,
dass ein Pentagondodekaeder entsteht, wenn man die Spitzen miteinander
verbindet. |
Die Bildpaare werden mit dem 3D-Blick dreidimensional.
... ... ... |
Der Bascetta -Stern ist verwandt mit dem Sonobe-Stern,
bei dem es sich auch um ein bekröntes Ikosaeder handelt und der auch
aus 30 Modulen zusammengesteckt wird. |
Falten
eines Moduls top
Material
... ... ... |
Man benötigt für den Stern 30 Quadrate aus
Papier.
Da bieten sich die Notizzettel 9cm x 9cm an, die man in
jedem Schreibwarengeschäft kaufen kann. |
11
Schritte
01
...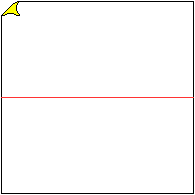 ... ... |
Halbiere das Quadrat mit einer Talfaltung.
Es ist günstig, dass man für diese Knickfaltung
und die folgenden nicht nur mit dem Finger über den Knick geht, sondern
z.B. mit einer umgekehrten Schere. |
02
...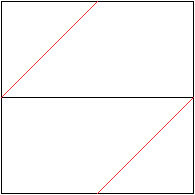 ... ... |
Falte an den roten Linien.
 |
03
...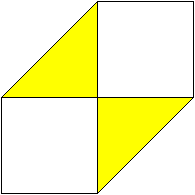 ... ... |
Das müsste dann so aussehen.
 |
04
...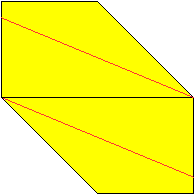 ... ... |
Drehe das Papier um und falte an den roten Linien.
 |
05
...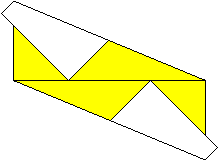 |
Das müsste dann so aussehen.
 |
06
...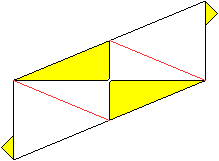 ... ... |
Drehe das Papier um und falte an den roten Linien.
 |
07
... ... ... |
Das müsste dann so aussehen.
 |
08
... ... ... |
Drehe das Papier um und falte an den roten Linien.
 |
09
... ... ... |
Das müsste dann so aussehen.
Falte an der roten Linie.
 |
10
...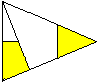 ..................... ..................... |
Das müsste dann so aussehen.
 |
11
...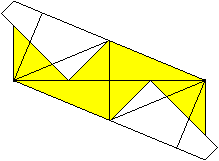 ... ... |
Entfalte das Dreieck mehrmals bis du wieder auf die Figur
05 gelangst. |
...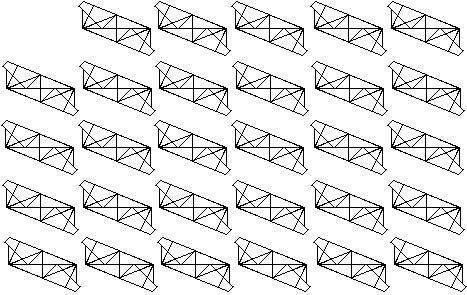 ... ... |
Da muss man durch.
Falte das Modul noch 29 x. |
...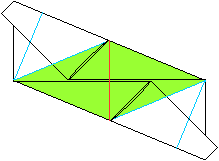 ... ... |
Es sei schon einmal angemerkt, dass jedes Modul zu zwei
Seitenflächen nebeneinander liegender Zacken beiträgt. |
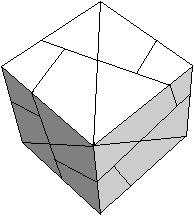
Zusammenfügen
zu einer Zacke top
...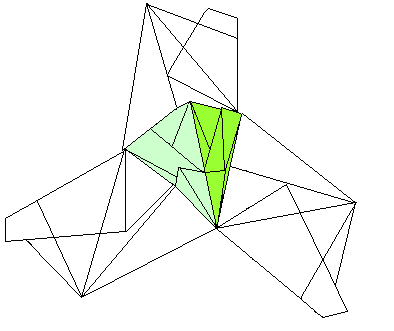 . . |
Drei Module steckt man zu einer Zacke zusammen. |
Und
das geht so.
...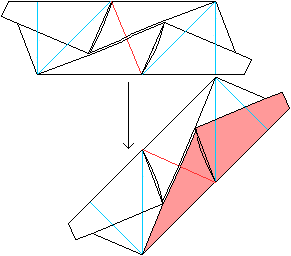 ... ... |
Stecke ein Modul in die (rosa) Tasche eines zweiten Moduls. |
...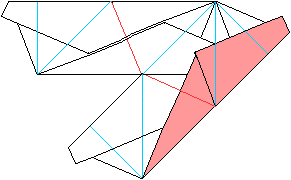 ... ... |
Das müsste dann so aussehen. |
...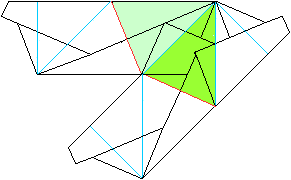 ... ... |
Das sind schon einmal zwei Seitenflächen einer Zacke.
Die obere Seitenfläche wird nach hinten weg geklappt.
Ein drittes Modul umfasst die beiden ersten und wird fixiert.
Die erste Zacke ist fertig. |
Zusammenbau des
Sterns top
An die erste Zacke werden nacheinander
Module, die jeweils eine weitere Zacke bilden, angefügt, bis der Stern
sich endlich schließt.
... ... ... |
Es ist in dem entstehenden Durcheinander eine große
Hilfe, wenn man sich das erzeugende Ikosaeder vorstellt:
An jedem Eckpunkt treffen fünf Dreiecke zusammen.
Für den Stern heißt das, dass immer
fünf Zacken einen Kranz bilden. |
Etwas Mathematik top
...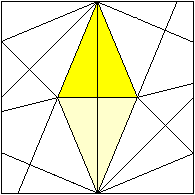 ... ... |
Entfaltet man das Modul, so erkennt man zwei Seitenflächen
von Zacken als gleichschenklige Dreiecke.
Der Winkel an der Spitze eines Dreiecks beträgt wegen
des Faltvorgangs 22,5°.
Die Höhe des Dreiecks ist die halbe Seitenlänge
des Quadrats. |
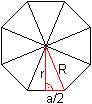
Der Winkel 22,5° tritt
auch im Grunddreieck des regelmäßigen
Achtecks auf.
... ... ...
|
Deshalb kann man die folgenden Formeln übernehmen.
Ist die Grundseite a gegeben, dann gilt
für die Höhe im Dreieck r = (1/2)[sqrt(2)+1]a
(gerundet r = 1,207a)
und für den Schenkel R = (1/2)sqrt[4+2sqrt(2)]a
(gerundet R = 1,307a). |
Auf drei Fragen
soll eingegangen werden.
1. Frage
Die Quadratfläche Aq
des Moduls wird nur zu einem kleinen Teil genutzt. Wie viel Prozent sind
das?
Antwort
Die beiden gleichschenkligen Dreiecke
haben zusammen den Flächeninhalt 2A = ar.
Das Quadrat des Moduls hat die
Fläche Aq = 4r².
Dann gilt (2A)/Aq =
(ar)/(4r²) = a/(4r) = 1/[2(sqrt(2)+1)] = (1/2)[sqrt(2)-1] = 0,207
= 20,7%.
Ergebnis
Etwa 20% der Fläche des Ausgangsquadrats
werden genutzt.
2.
Frage
Wie groß ist die Höhe
H einer Zacke?
Antwort
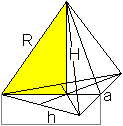 |
Nach dem Satz des Pythagoras gilt
H² = (1/4)[4+2sqrt(2)]a²-[(2/3)(1/2)sqrt(3)]²a²
= [1+(1/2)sqrt(2)-1/3]a² = [2/3+(1/2)sqrt(2)]a²
= (1/36)[24+18sqrt(2)]a²
Dann ist H = (1/6)sqrt[24+18sqrt(2)]a (gerundet H = 1,172a) |
Ergebnis
Die Höhe einer Zacke beträgt H = (1/6)sqrt[24+18sqrt(2)]a
(gerundet 1,172a).
Die Höhe der Zacke des
Großen
Sterndodekaeders beträgt nach der Webseite von de.wikipedia
k = (1/6)[3sqrt(3)+sqrt(15)] = 1,516a, ist also größer
als die Zacke des Bascetta-Sterns.
3.
Frage
Wie groß ist der Stern?
Damit ist die Entfernung e der Spitzen zweier gegenüber
liegender Zacken gemeint.
Antwort
> Der Abstand gegenüberliegender Seitenflächen
des Ikosaeders ist d=(1/6)[3sqrt(3)+sqrt(15)]a =1,152a.
> Die Höhe einer Zacke ist H = (1/6)sqrt[24+18sqrt(2)]a
= 1,172a
Dann ist e = 2H+d = (1/3)sqrt[24+18sqrt(2)]a+(1/6)[3sqrt(3)+sqrt(15)]a
(gerundet e = 3,496a).
Es ist günstig, die Entfernung e auf die Seitenlänge
2r des Ausgangsquadrates zu beziehen.
Es gilt r = 1,207a oder a = 0,829r. Dann ist e = 3,496a
= 3,496*0,829r = 2,898r = 1,450(2r).
Mit 2r = 9cm ist e = 13,04cm.
Ergebnisse
Ist die Seitenlänge des Ausgangsquadrates 9cm, so
wird der Stern 13,04 cm groß.
Das Verhältnis e/(2r) ist 1,45. Der Stern ist etwa
50% größer als die Seitenlänge des Quadrats.
Weitere
Körper aus den Modulen top
Rudolf Kunstmann, der die Anregung zu dieser Webseite
gab, hat sich offenbar intensiv mit Körpern aus den Bascetta-Modulen
nebst Varianten beschäftigt. Mit seinem Einverständnis zeige
ich eine kleine Auswahl seiner Sterne.
Sterntetraeder
Stern
zum Kuboktaeder
Stern zum Kleinen Rhombenkuboktaeder
Stern
zum abgeschrägten Würfel
Körper
aus anderen Modulen top
Auf meiner Webseite Körper
flechten verwende ich andere Module, um einen Würfel zu bauen.
Modulares Origami oder (englisch) modular Origami
ist ein weites Gebiet, zu dem man in Literatur und Internet viel findet.
Bekrönte Polyeder
top
Bekrönte Polyeder (oder sollte ich schreiben gekrönte
oder gar gehörnte Polyeder?) sind konvexe Polyeder, auf dessen
Seitenflächen gerade Pyramiden stehen. Im Englischen heißen
sie so schön stellated polyhedra.
Körper dieser Art, die auf meiner Homepage zu finden
sind, habe ich einmal zusammengestellt.
Bekröntes
Tetraeder
Hypertetraeder
Bekröntes
Oktaeder
 ... ...
Rhombendodekaeder
Bekrönter
Würfel
Bekröntes
Ikosaeder und bekröntes Pentagondodekaeder
Bekröntes
Rhombendodekaeder
Bekröntes
Kleines Rhombenkuboktaeder
...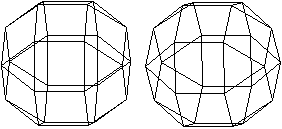 ..... ..... |
Bekrönt man ein kleines
Rhombenkuboktaeder, so entsteht ein Stern aus 18 quadratischen Zacken
und acht dreieckigen.
Das ist die Form des bekannten Herrnhuter Stern. |
... |
Das ist der Herrnhuter Stern, gebaut aus einem Bausatz
(12/2013). |
Es gibt jetzt (05/2022) eine
weitere Webseite zu einem bekrönten Ikosaeder aus 20 Quadraten, dem
Kusudama-Stern.
Vergleich
dreier Sterne
|
a=9,0cm
|
Sonobe-Stern
|
Bascetta-Stern
|
Kusudama-Stern
|
|
2A/Aq
|
12,7%
|
20,0%
|
26,8%
|
|
H
|
0,29a = 2,6cm
|
0,49a = 4,4cm
|
0,70a = 6,3cm
|
|
e
|
1,04a = 9,4 cm
|
1,45a = 13,1cm
|
1,97a = 17,7cm
|
|
Sonobe Star
|
Bascetta Star
|
Kusudama Star
|
|

|
|
Bascetta-Stern
im Internet top
Deutsch
Annerose Gemeinhardt
Bascetta
Stern (.pdf-Datei)
Paolo
Bascetta ist bei Facebook.
Stephanie Meschke
3d-Stern,
Sonobe-Stern
(.pdf Dateien)
Wikipedia
Bascetta-Stern,
Sternkörper,
Herrnhuter
Stern,
Weihnachtsstern
(Symbol)
Englisch
Jim Plank
Jim
Plank's Origami Page (Modular)
Jo Nakashima
Origami
Bascetta Star (Video)
Origami-Resource-Center.com
Sonobe
Stellated Octahedron (12 units)
Wikipedia
Sonobe,
Moravian
star,
Star polyhedron,
Polyhedral
compound, Modular
origami, Mitsonobu
Sonobe
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2012 Jürgen Köller
top |

 ...
...
 ...
...

 ...
... ...
... ...
... ...
... ...
... ...
... ...
...
 ...
... ...
... ...
... ...
... .....................
..................... ...
... ...
... ...
... .
. ...
... ...
... ...
... ...
... ...
...












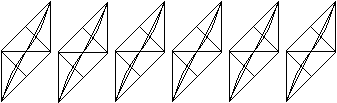


 .....
.....

