Sonobe-Stern
Inhalt dieser Seite
Was ist der Sonobe-Stern?
Falten des Sonobe-Moduls
Bau des Sonobe-Sterns
Weitere Körper		 Etwas Mathematik
Variante des Sonobe-Moduls
Sonobe-Stern im Internet
.
Zur Hauptseite    "Mathematische Basteleien"

Was ist Sonobe-Stern?
...... Der Sonobe-Stern ist ein dreidimensionaler Stern, der aus 30 Modulen zusammengesteckt wird. 

Die Module werden aus Quadraten gefaltet.

Mathematisch gesehen ist er ein Ikosaeder, auf dessen Seitenflächen 20 dreiseitige Pyramiden stehen.

Der Name geht auf den den japanischen Origami-Enthusiasten Mitsunobu Sonobe zurück.

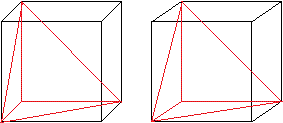...... Die Zacken sind genauer rechtwinklige dreiseitige Pyramiden. 
Sie treten z.B. bei einem Würfel an einer Ecke auf. 
Bei einer rechtwinkligen Pyramide treffen an der Spitze drei kongruente rechtwinklig-gleichschenklige  Dreiecke aufeinander. Die Grundfläche ist ein gleichseitiges Dreieck.

......
Der Sonobe-Stern ist verwandt mit dem Bascetta-Stern, bei dem es sich auch um ein bekröntes Ikosaeder handelt und der auch aus 30 Modulen zusammengesteckt wird. 

Falten des Sonobe-Moduls       top
Material
...... Man benötigt für den Stern 30 Quadrate aus Papier.

Da bieten sich die Notizzettel 9cm x 9cm an, die man z.B. in Schreibwarengeschäften kaufen kann.

Neun Schritte
1
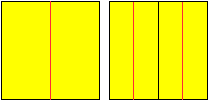...... Teile das quadratische Blatt durch dreimaliges Falten in vier gleiche Längsstreifen.

2
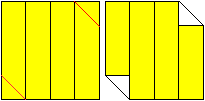...... Falte an den roten Linien und du erhältst die rechte Figur.
3
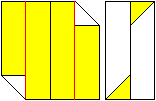...... Falte an den roten Linien und du erhältst die rechte Figur.
4
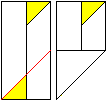...... Falte an der roten Linie und du erhältst die rechte Figur.
5
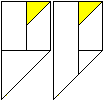...... Mache die Faltung rückgängig und stecke das rechte untere Dreieck unter den linken Längsstreifen.
Das müsste dann so aussehen wie in der rechten Figur.
6
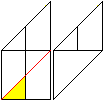... Drehe das Blatt um 180° und falte an der roten Linie. Du erhältst die rechte Figur.
7
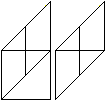... Mache die Faltung rückgängig und stecke das rechte untere Dreieck unter den linken Längsstreifen.
Du erhälst die rechte Figur. 
8
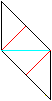
...... Drehe die Figur um.
Falte an den roten Linien und an der blauen Linie.
Entfalte wieder.
9
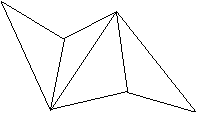... Das ist das Sonobe-Modul.

Bau des Sonobe-Sterns top
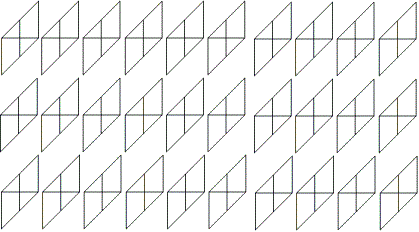...... Für den Sonobe-Stern benötigt man 30 Module.

Keine Angst, das Modul ist einfach zu falten.

......
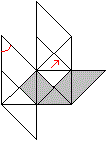Man steckt zuerst drei Module ineinander und formt eine Würfelecke, 
indem man die rot gekennzeichnete Spitze in eine Tasche schiebt.
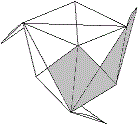...... Das ist der Blick auf die Würfelecke.
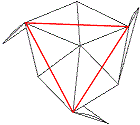...... Man faltet an den roten Linien und formt so eine rechtwinklige Pyramide mit einem gleichseitigen Dreieck als Grundfläche.
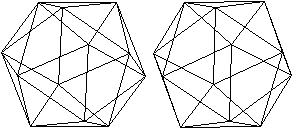
An die erste Zacke werden nacheinander die Module angefügt, bis der Stern sich endlich schließt. 
...... Es ist in dem entstehenden Durcheinander eine große Hilfe, wenn man sich das erzeugende Ikosaeder vorstellt: An jedem Eckpunkt treffen fünf Dreiecke zusammen. 

Für den Stern heißt das, dass immer fünf Zacken einen Kranz bilden.
...... Das erkennt man auch auf dem Foto des fertigen Sterns.

Klasse VAB 2S der Justus-von-Liebig-Schule in Mannheim, 2015

Weitere Körper   top
Bau eines Oktaeder-Sterns
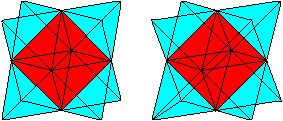...... Der Oktaeder-Stern entsteht, wenn man auf die acht Seitenflächen eines Oktaeders Tetraeder setzt.

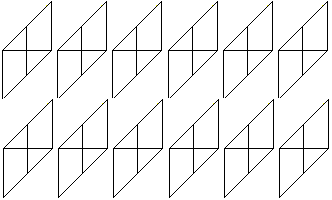...... Für eine Variante des Oktaeder-Sterns benötigt man 12 Module.

Aus den Tetraedern werden rechtwinklige dreiseitige Pyramiden. 
...... Das ist der Stern.

Er wird wie der Sonobe-Stern zusammengesteckt. 

Man muss nur darauf achten, dass nicht fünf Zacken, sondern vier Zacken einen Kranz bilden.
Bau eines Sonobe-Würfels
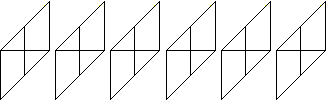...... Für einen Würfel braucht man sechs Module.
......
Man steckt zuerst drei Module ineinander und formt eine Würfelecke, 
indem man die rot gekennzeichnete Spitze in eine Tasche schiebt.
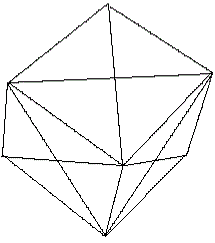
...... Das ist der Blick auf eine Würfelecke.

Man fügt nacheinander die drei übrigen Module hinzu und gelangt schließlich zum Sonobe-Würfel.
......
Bau eines bekrönten Kuboktaeders
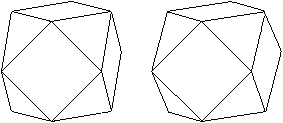...... Das Kuboktaeder ist ein archimedischer Körper, der von acht gleichseitigen Dreiecken und sechs Quadraten gebildet wird. Die Sonobe-Module gestatten es, es zu bekrönen. 
...... Baut man diesen Körper aus 24 Modulen nach, so ist das Ergebnis enttäuschend. Er ähnelt einem Würfel, da die quadratischen Pyramiden sehr flach sind.
Spielereien mit Würfeln
... Zwei Würfel durchdringen sich

Würfel mit Doppelpyramide Huckepack

Doppelwürfel

Etwas Mathematik top
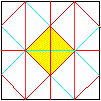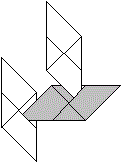
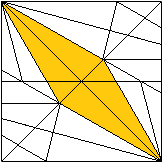
... Entfaltet man das Sonobe-Modul, entsteht ein Muster aus gleichschenklig-rechtwinkligen Dreiecken. 
Das gelb gefärbte Dreieck entspricht der Seitenfläche einer rechtwinkligen Pyramide.
Jedes Modul ist an der Bildung dreier Zacken beteiligt. 

Zwei Fragen interessieren. 
1 Die Fläche eines Moduls wird nur zu einem kleinen Teil für eine Zacke genutzt. Es liegen Schichten übereinander.
Wie groß ist die Oberfläche O2 des Sonobe-Sterns im Verhältnis zur Gesamtfläche O1 der 30 Ausgangsquadrate?
Rechnung
Es sei a die Länge der Quadratseite, dann ist die Seitenlänge des Grunddreiecks einer Zacke (1/2)a. 

Die Gesamtfläche aller Blätter O1 = 30a².

Die Seitenfläche einer rechtwinkligen Pyramide ist (1/16)a².
Die Summe aller Seitenflächen oder die Oberfläche des Sterns ist dann O2 = 20*3*(1/16)a² = (1/4)*15a².
Das Verhältnis O2:O1 ist [(1/4)*15a²]:[30a²] = 1/8 = 0,125 = 12,5 %.
Ergebnis
Nur zu 12,5 % wird das Papier genutzt.

2 Wie groß wird der Sonobe-Stern, wenn das Ausgangsquadrat die Seitenlänge a hat. 
Die Größe des Sterns soll durch die Entfernung e zweier gegenüber liegender Spitzen angegeben werden.
Rechnung
Die Entfernung ist die Summe zweier Höhen H der rechtwinkligen Pyramiden und dem Abstand d gegenüber liegender Seitenflächen des Ikosaeders, e = 2H+d.
Auf meiner Webseite dreiseitige Pyramide findet man H=(1/3)sqrt(3)*(1/2)a.
Auf meiner Webseite Bascetta-Stern findet man d=(1/6)[3sqrt(3)+sqrt(15)](1/2)a.

Das heißt e = (1/3)sqrt(3)a+(1/6)[3sqrt(3)+sqrt(15)](1/2)a = [(5/12)sqrt(3)+(1/12)sqrt(15)]a  = (1/12)[5sqrt(3)+sqrt(15)]a
oder gerundet e = 1,044a.
Ergebnis
Ist a die Seitenlänge des quadratischen Blattes Papier, so ist der Sonobe-Stern e = 1,044a groß.
Ist a= 9 cm, so ist e = 9,40 cm.

Variante des Sonobe-Moduls     top
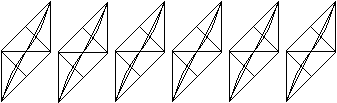...... Ich kenne noch eine Variante des Sonobe-Moduls, bei der eine zusätzliche Faltung nötig ist. Das Modul hat den Vorteil, dass es stabiler ist. Drei Module bilden eine Bipyramide, sechs einen Würfel. - Näheres findet man über die beiden Links.


Beaded Origami Ornament

Sonobe-Würfel
Es gibt jetzt (05/2022) eine weitere Webseite zu einem bekrönten Ikosaeder aus 20 Quadraten, dem Kusudama-Stern. 
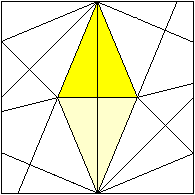
Vergleich dreier Sterne
a=9,0cm
Sonobe-Stern
Bascetta-Stern
Kusudama-Stern
2A/Aq
12,7%
20,0%
26,8%
H
0,29a = 2,6cm
0,49a = 4,4cm
0,70a = 6,3cm
e
1,04a = 9,4 cm
1,45a = 13,1cm
1,97a = 17,7cm
Sonobe Star
Bascetta Star
Kusudama Star

Sonobe-Stern im Internet    top

German

greifswalderfalterstammtisch 
Sonobe-Modul   (mit Somawürfel)

English

Origami-Resource-Center.com
Sonobe Stellated Octahedron (12 units)

wikiHow
How to Make a Sonobe Unit

Wikipedia
Sonobe

Youtube
Origami Modular Sonobe Unit, Sonobe instructions
Youtube

DIY - Stern Oktaeder Papier   (Google Übersetzer)
Auch wenn ich die russische Kommentatorin nicht verstehen konnte, gelang der Oktaederstern auf Anhieb. Die Zacken sind  rechtwinklige dreiseitige Pyramiden. Deshalb erscheint dieser Link auf dieser Seite.
Er wird aus einem quadratischen Blatt (A4 zuschneiden!) gefaltet. 

Feedback: Emailadresse auf meiner Hauptseite

Diese Seite ist jetzt auch in Englisch vorhanden.

URL meiner Homepage:
http://www.mathematische-basteleien.de/

©  2015 Jürgen Köller 

top