|
What is a Square?
... . |
A square is a four-sided figure with four right angles
and four equal sides. |
... .... |
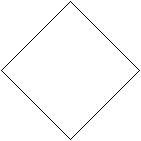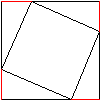
The same figure stands on one corner.
It is called a diamond to express the new position of
the square. |
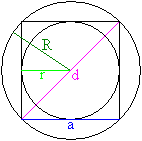
Variables of
the Square top
The square has four equal sides.
Two sides meet in one corner and
are perpendicular to each other.
... ...
|
The length of a side is a.
The square has two diagonals of
the length d=a*sqr(2).
The area is A=a², the perimeter
is U=4a.
The circumscribed circle has the radius R=sqrt(2)/2*a,
the inscribed circle the radius r=a/2. |
Only one Formula top
... |
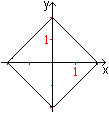It is possible to describe a square by only one
formula in a coordinate system.
|x|+|y|=2 or abs(x)+abs(y)=2
|
Square Numbers
top
You get square numbers if you multiply natural numbers
by themselves.
... ... |
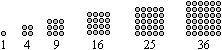The square numbers can be illustrated by squares. |
... |
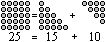Each square number is the sum of two triangular numbers.
Formula: n²=[1+2+3+...+n] + [1+2+3+...+(n-1)] |
... |
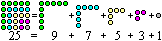Each square number n² is the sum of the n first
odd numbers.
Formula: n²=1+3+5+...+(2*n-1) |
... |
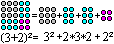You can divide a square into two smaller squares and
two equal rectangles.
There is the first binomial theorem (a+b)²=a²+2*a*b+b². |
... ... |
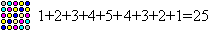You can divide a square into strips in a diagonal direction.
There is 1+2+3+...+n+...3+2+1=n².
 |
Divide a Square
in Half top
There are many possibilities to
halve the area of a square. Here are five.
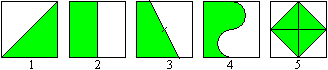To 1 and 2: The common way is dividing the square by a diagonal
or a median. So you can fold a square sheet of paper.
To 3: Each straight line going through the centre of
a square cuts it in two congruent trapeziums.
To 4: You can also use other lines like half circles
instead of straight lines.
To 5: The figure in the middle consists of four congruent
triangles, the whole figure of 8 ones. So the halving is clear. If
the start square has the area 2, green square has the area 1 and the length
sqrt(2). The importance of this figure is the fact that the outer square
has a rational, the inner one an irrational length.
Square inside
a Square top
... .... |
If you measure a line (red) starting in a corner and
going in one direction you get four points. If you connect them you get
a square.
Proof: The four triangles are congruent because of the
theorem side/angle/side. The angle is the right angle in the middle. Thus
the hypotenuses are equal and they are the sides of the figure. Its angles
are 90°. |
Square and Circle
top
 |
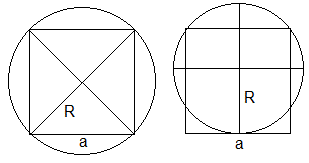In the drawing on the right, a circle goes through all
four corners of a square.
This is the circumcircle with R=(1/2)sqrt(2)a or approximately
0.7a.
In the left drawing a circle goes through two corners
and touches one side.
According to the geometric mean theorem, the radius is
R=(5/8)a or about 0.6a.
|
Sequence of Squares
top
... ... |
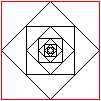The red square has the side length a and thus the area
a².
One the other side there is the sum of all inner squares:
A= a²/2 + a²/4+a²/8+a²/16+... = a²(1/2+1/4+1/8+1/16+...).
The series in brackets is geometric. It has the limit
1. |
Result: The sum of the areas of the inner squares approaches
the area of the whole square.
The binomial and the Pythagorean
theorems use squares.
You find more on my page Illustrations
of Formulas.
Tiling the Square
top
It is easy to divide a square in equal squares. It is
difficult to find different squares which can do that.
... ... |
You need at least 21 different squares which form a square
(Duijvestijn 1962, 1978).
Solution:
112² = 50²+42²+37²+35²+33²+29²+27²+25²+24²+19²+18²+17²+16²+15²+11²+9²+8²+7²+6²+4²+2² |
Many mathematicians (and their computers) worked on that
problem (Book 2). You find more on Erich Friedman's web site (URL below).
An Infinite
Geometric Series top
... |
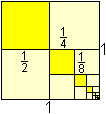The geometric progression 1/4+1/16+1/64+ ... has the
limit 1/3.
Proof: s=a[1/(1-r)]=(1/4)[1/(1-(1/4)]=1/3
There is a remarkable picture on the left.
Found at bei http://en.wikipedia.org/wiki/The_Quadrature_of_the_Parabola |
Largest
and Smallest Rectangles top
The square is a special rectangle. You can see that in
the following solutions of extremum problems.
Problem 1) Which rectangle of equal perimeters has the
largest area?
Problem 2) Which rectangle of equal areas has the smallest
perimeter?
Problem 3) Which rectangle of an equilateral triangle
has the largest area?
Problem 4) Which rectangle inside a square has the largest
area?
Problem 5) Which rectangle inside a circle has
the largest area?
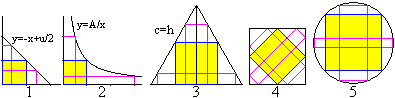In all cases a square is the searched rectangle.
You find the largest square inside a cube on my cube
page.
Writing Digits top
Matrix of squares
... ....
|
The pixels used for writing letters of fonts form a small
matrix square, which you can only see with sufficient magnification.
You use a matrix 9x14 for the picture of the digit 2
in the font "Times New Roman"of Winword. |
.. ....
|
... ... |
If you double a square, you get a form, which is able
to show all ten digits.
This is well known from the calculator. |
.. ....
|
Solomon's
ring
... .... |
In an old legend Lucas tells that a square with diagonals
was engraved in one of Solomon's rings.
The ten digits are hidden here [Book 1]. |
.. ....
|
Keyboard of
a calculator
... ... |
You can also take the keyboard of a calculator as an
example. The numbers 1 to 9 are on square keys. Altogether they form a
3x3 square. It is strange that the numbers go from right to left and from
the bottom to the top. The numbers on the keyboard of a telephone run like
our writing.
I remember that people tried to find a standardized order
of the keyboard for telephone and calculator. That went wrong. The first
cheap calculators came from the Far East and they took their order.
Some nostalgia: I still have a calculator from 1971 (Quelle
"Privileg"), which has been working until now (2004). The price was 300
DM (about 150 Euro). It used 220V for glow lamps for showing the numbers.
It didn't know the rule "multiplying first, adding second" and didn't show
the front zeros. |
Looking back this calculator was a big help and saved much
time ;-).
Optical Illusions
top
You see: The squares on the left are different in their
side lengths, those on the right in their areas.
You already supposed: The squares have the same measurements.
You see: Four four-sided figures
lie in front of a sequence of circles, squares, or straight lines. The
sides look bent.
You already supposed: There are congruent squares.
You see: Both grids have grey spots at the crossing
points.
You already supposed: The grey spots are imagination.
An arrangement of four 3/4 circles
... |
There is no square drawn, in spite of that you see it. |
Polyominos top
You can arrange squares for complex
figures. You demand that two squares always touch in one side.
The figures are counted up to 28-ominos. Look at the last
line.
This is a possible
way to the Pentominos.
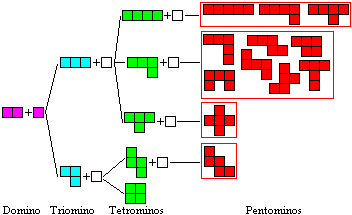
You find more on my pages Domino
Puzzle,
Pentominos und Hexominos.
If you also admit 3d-figures, you
get monoids.
... ... |
You give three squares for example. You can built eight
3d-monoids except the two triominos. |
You find more on my page Rubik's
Magic. There are many figures of eight squares.
There is a systematic investigation of the monoids on
Jorge L. Mireles Jasso's web site (URL below).
Games and Squares top
If you look at the most common games under square views,
you are successful. Nearly all games use squares in the board, the playing
field, or the peg.
I only list all the games which I describe on other places
of my homepage:
Domino Puzzle, Froebel
Star, 15Puzzle, Fortune
Teller, Magic Square, Peg
Solitaire
Squares on the
Internet top
German
Wikipedia
Quadrat
English
Eric W. Weisstein (MathWorld)
Square,
Square
Packing,
Perfect
Square Dissection
Erich Friedman
Erich's
packing center
Kevin L. Gong
counting
polyominoes
Kevin L. Gong
counting
polyominoes
Wikipedia
Square
References top
(1) Walter Lietzmann: Lustiges und Merkwürdiges
von Zahlen und Formen, Göttingen 1969
(2) Friedrich L. Bauer: Einladung zur Mathematik, Deutsches
Museum, München 1999
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
2004 Jürgen Köller
top |
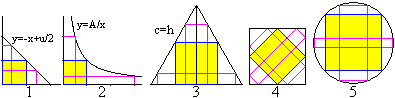
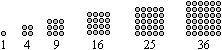