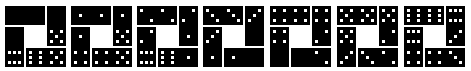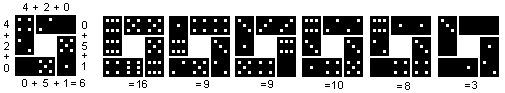|
What is Domino?
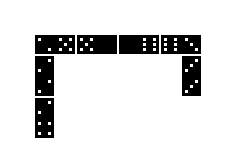 |
Domino is a famous game with domino pieces (shorter
dominos). Two or more players must alternately lay fitting pieces. The
winner is the person who gets rid of all his pieces first.
Here you see a picture of the first phase of the play. |
I won't go into details now. I shall describe puzzles with
dominos and then only with all its 28 pieces.
Domino Pieces
top
You need eight sequences of seven squares for the pieces
(down left). Altogether there are 56 squares. They show the numbers 0 to
6. The numbers are represented by patterns you find on dice. An empty square
takes the place of the number 0.
Two squares form a domino (above on the right). So you get
1+2+3+4+5+6+7=28 dominos.
Figures from Dominostop
Laying figures is a popular activity with dominos. Dominos
with the same number of points must meet like with the normal domino game.
- You usually limit to symmetrical patterns.
1st example:
... |
You can easily make a square framework 15x15 from all
dominos. |
2nd and 3rd examples: Symmetrical
figures with axis and centre point
top
You should lay the crossings first. There you need 3 squares
with the same number of points. Therefore you must use dominos with the
same number of points also for another crossing, because there are 6*2
squares altogether.
4th example: A symmetrical figure
with one axis
5th example: Symmetrical figures
with a centre point (Book 2 or book 3)
... ... ... |
This is a well-known figure, which you can form with
all the 28 dominos.
You get more patterns, if you reflect the figure, or,
this is more interesting, if you permutate the numbers of points on the
dominos. You can replace the squares (0,1,2,3,4,5,6) by the squares (3,5,1,0,6,2,4)
for example. |
6th example: Variation of
the third example
... |
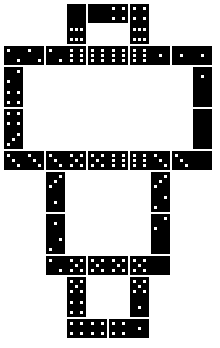
Valerio Bianconi from Italy sent me a solution of a new
figure. |
Quadrilles
top
... ... ... |
Quadrilles go back to the French mathematician
Edouard Lucas (1842-1891). Those are compact figures with all 28 dominos.
2x2squares with the same numbers of points are included in. Here
is an example. |
Seven Squares
top
1st problem:
You can lay seven square frames with all the 28 dominos.
Dominos with the same number of points meet.
2nd problem:
You can lay seven square frames with all the 28 dominos,
so that the sums of the numbers of points are the same at all four sides
(book 1).
The simple square frame 15x15 from the top also has the
feature of the same sum at all four sides. The sum is (1+2+3+4+5+6)*8/4
= 44.
Making pairs
top
 |
You give a 7-8-matrix with the numbers 0 to 6, each number
eight times. These are the squares, which the dominos have.
The problem is to assemble two squares lying underneath
the other or side by side. |
Tip: You should find the dominos with
the same number ("doublets") first.
This
is a solution.

You can invent this kind of puzzle yourself.
Dominos on the
Internet top
Englisch
James Masters (tradgames.org.uk)
Dominoes
Teun Spaans
Domino
Plaza
Wikipedia
Dominoes
Deutsch
Otto Janko
Domino-Puzzles
Wikipedia
Domino
(Spiel)
Polnisch
Lamiglówki Mix
Domino
Russisch
Leonid Mochalov [PUZZLES of LEONID MOCHALOV]
DOMINO
SOLITAIRE, Puzzles
with Dominoes (translated to English)
References
top
(1) Walter Sperling: Auf du und du mit Zahlen, Rüschlikon-Zürich
1955
(2) Pieter van Delft, Jack Botermans: Denkspiele der
Welt, München 1980
(3) Karl-Heinz Koch: ...lege Spiele, Köln 1987 (dumont
taschenbuch1480)
(4) Martin Gardner: Mathematischer Zirkus, Frankfurt
a.M. 1988
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
http://www.mathematische-basteleien.de/
©
2000 Jürgen Köller
top |






 ...
...
 ...
...