|
What is Rubik's Magic? top
... ... |
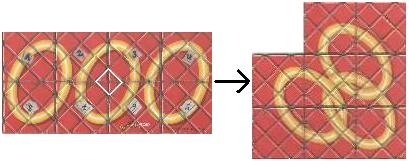Rubik's Magic is a folding game for one person.
A rectangle of 4x2 squares is to be changed to a six-cornered polygon
in heart shape by a sequence of foldings.
At the same time three separate rings change into three linked rings
on the reverse side. |
... ... |
The first Magic of Matchbox from the 1980s is black and has the same
rings. They are more beautiful because of the rainbow colours.
The black Magic rectangle stands on its head compared with the red one.
|
Description top
.. .... |
When you buy Rubik's Magic, you get it as a 4x2-rectangle with the
three rings. After several random foldings some squares lie on each other.
If you stretch Magic you find strange three-dimensional configurations.
Sometimes squares even penetrate each other. |
... ... |
.. .... |
If you put a rectangle on its head, it looks the same. If you take
into account the writing "Rubik's Magic", you can say: Magic stands upright,
if the words stand upright. The black Magic stands upright, if the words
stand upside down. |
... ... |
The reverse side of Magic has disordered squares.
There is one unique square: It has three arcs. Here it is marked yellow.
If you have solved Magic, this square goes into the centre. |
If you play with Magic and you want to control your movings, you can look
at the three-arcs-square (Book 3).
I prefer numbering the squares (Similar to book 2).
... ... |
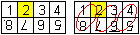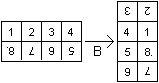
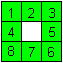
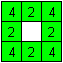
I suggest numbering the squares as shown at the drawing on the left.
Then there is a ring with eight squares, where the numbers stand upright. |
... ... |
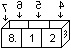The centre diamond
... ... |
This is important to understand the following sequences:
The 4x2-rectangle has a diamond formed by groves on four squares on
both sides.
If there are strings in it, it is drawn as shown on the right. |
... ... |
Sequences top
If you have mixed the Magic up, you must try to find any 4x2 rectangle.
If you succeeded, you should try the following sequences.
Ring
|
You quickly find out: You can open each rectangle to a ring. |
Changing the rows
(Sequence A)
This sequence has the effect that two lines interchange. The writing
"Rubik's Magic" stands horizontally as before.
If you repeat the sequences you return to the start pattern. The sequence
has the order 2. - The moves are reversible.
Turning the squares
(Sequence B)
The squares are ordered in another way at the same
time. The writing "Rubik's Magic" stands horizontally before and
vertically after making the moves.
If you repeat the sequences you return to the start pattern. The sequence
has the order 2. - The moves are reversible.
Transformation
By the way: The right 2x2 square doesn't move during this procedure.
All Patterns of Eight
Squares top
... ... |
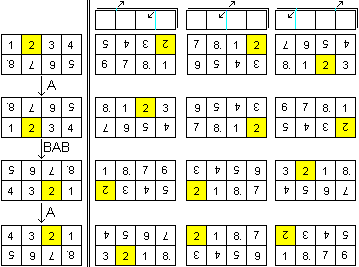How many patterns can you make with the squares?
First observation: The sequence of the squares 1 to 8 is kept at every
pattern.
There are four main patterns (left row), which turn into each other
by the given sequences A and BAB.
You can find three more to every main pattern by using the main squares
and the sequences below. |
There are 16 patterns of the 4x2 rectangle.
... ...
|
If you perform B at any 4x2 rectangle, you get different 2x4 rectangles.
Thus there must also be 16 rectangles of this kind.
|
Result: There are 32 patterns of 8 squares altogether.
A Solution top
First Step
|
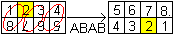
Change the basic rectangle to a rectangle with 1 in the right corner
at the second row. |
Second Step
|
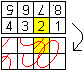
Turn the rectangle as shown on the left. Use the tansformation. |
Transformation
A shorter Solution
... |
... |
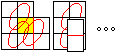Use a "mirror" version of the transformation for the heart shaped form.
You get the rectangle with the three rings by the sequences B and C1.
The reverse path is a solution. |
The Mechanism of Folding top
The first impression is that every piece has two hinges like the Jacob's
ladder toy. This is partly right. The mechanism is more complicated however.
If you lay two squares on top of each other, then a new hinge appears
at the right angle to the old hinge. |
... ... |
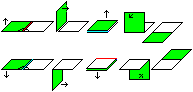Where the hinge is depends on folding up or down. In the drawing strings
are on the top in front.
The Labyrinth of Strings top
... ... |
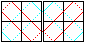Two adjacent squares are connected with strings, actually by two rings
of fishing line. You see them running in grooves partly in front or behind
the squares. If you lay two squares on top of each other, then strings
jump into empty grooves of the opposite square. |
The following description refers to the
ring with the ordered squares.
... ...
|
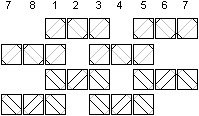The eight squares are connected by 2x8 strings.
One pair of rings goes through three squares. |
There are four strings in the grooves of squares 1,3,5, and 7, and there
are two strings in the grooves of the squares 2,4,6, and 8. The squares
are not of the same kind. If a string gets snarled up in one place (it
can happen!), you can cut one string in a groove, which has two strings,
and remove it. You can fold Magic in spite of that, in fact it is even
better. But don't cut the strings without having to do so. Better safe
than sorry.
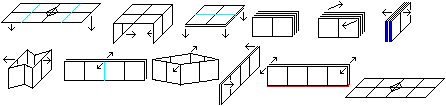
Shapes top
Double square-figures
... ... |
There are also the plane shapes on the left, which you can form with
4+4 squares. The T-form is missing.
If you stretch these shapes you find different 3D configurations. "L"
especially is productive. |
Though the sequence 1 to 8 is kept, strange shapes will develop, because
the squares penetrate (also several times) each other.
Cube
Folding the cube is a special challenge.
... ..
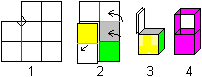Be careful!.
|
1 Start with the heart-like shape. Fold at the red lines.
2 Spread out the figure uand turn it at the same time. Watch at valleys
and mountains.The two squares above stay above. The three right squares
turn in direction of the arrows.
3 A cube arises.
4 You can lift the square at the top and you get a basket. |
 |
... ... |
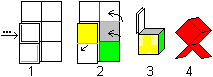The cube is nicer, if it stands on two squares.
The dark blue lines give the position of the hinges.
But the way to figure 1 is long... (Book 3) |
Symmetric Cubic Shapes
There are many shapes, which you can find by accident. I restrict myself
to symmetrical shapes, the squares of which are perpendicular to each other
and which have no double walls because of their multitude and their "beauty".
I ordered the shapes from two points of view:
(1) The colour indicates the smallest rectangular solid (on the left)
you can lay round the shape ("wrapping solid").
(2) The number below the shape is the number of the squares the solid
and the shape have in common.
Did I find all shapes?
Polyominoids top
You call figures of connected squares lying in cubic lattices polyominoids
.
Jorge L. Mireles Jasso worked on these figures. He offers a program
on the internet, which can find, show and count polyominoids (URL see below).
I used this program for figures with eight squares because of Magic. You
get the large number of 207265 figures, which are ordered by the
form of the wrapping rectangular solid.
You can find much fewer shapes with Magic. There
is a considerable reduction. You can explain that by square 3, which is
in place of one of the eight squares.
1st reduction:
|
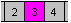
Each square has exactly two neighbour squares. |
This means the sequence of the squares is kept.
2nd reduction:
... ... |
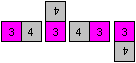In Magic there are only four places for a neighbour square.
Square 4 "rolls" around square 3. |
... ... |
Theoretically there are 16 possibilities for laying square number 4 to
square number 3. If you turn number 4, you even get 32 cases.
Impossible Figures top
... ...
|
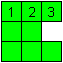It is easy to understand that this figure can't be solved with Magic.
There is no chain. Square 3 has no second neighbour.
 |
The next case is difficult to investigate.
Rule:
Go around the figure in a closed line. Start at a square and go back
to it. Calculate a sum step by step. Start with nought.
>If you leave a square having four strings and go to the right,
add 1. If you go to the left, subtract 1.
>If you leave a square having two strings and go to the right,
subtract 1. If you go to the left, add 1.
>If you go straight, the sum doesn't change.
If the sum is 0 in the end, the figure is possible with the 4x2-Magic.
... ...
|
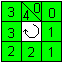Here the sum is 4 (-4 respectively)
|
Rubik's Magic Master Edition
top
. ..
|
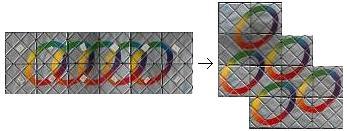There is a version of Magic with 12 squares in black or grey. You can
transfer moves, but there are also new ones. The figures are more complicated.
You can find a solution of the problem on the left in Christian Eggermont's
Homepage. He has the black Magic. You must turn the grey Magic at the beginning,
so that the writing is upside down. |
Purchase of Rubik's Magic
top
In Germany you can buy Rubik's Magic in every good toy shop.
You pay about 10€ (2004).
Copyright Jumbo International, Amsterdam. "Rubik's Cube is a trademark
of Seven Towns Ltd. used under licence".
Rubik's Magic on the
Internet top
German
Ronald Bieber
Lösung
Wikipedia
Rubik's
Magic
English
Christian Eggermont
Rubik's
Magic
Courtney McFarren (Mathematica)
Rubik's
Magic I
Rubik's
Magic II
http://www.rubiks.com/
Rubik's
Magic Puzzle
Jaap Scherphuis
Rubik's Magic Main
Page
Jorge L. Mireles Jasso
The
Minoids Applet
Maarten Vermaak
Folding
Puzzles
Rubik
on-line
Wikipedia
Rubik's Magic
Spanish
Javier Santos
Rubik's
Magic
References top
(1) Christoph Bandelow: Rubik's magische Ringe, Niedernhausen/Ts. 1986
(2) Ashwin Belur, Blair Whitaker: Rubik's Magic, München 1986
(3) James G. Nourse: Simple Solutions to Rubik's Magic, New York 1986
(4) Wolfgang Glebe: Mathematische Spielereien, Wissenschaftsmagazin
der TU Berlin Heft 10, 1991, Seite 94ff.
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
http://www.mathematische-basteleien.de/
©
2000 Jürgen Köller
top |
...
...