What is the 15 Puzzle?
.. 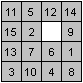 .. .. |
The fifteen puzzle has 15 pieces, which are numbered
from 1 to 15 and which lay in a square frame.
You cannot take away the pieces; you slide them by using
a free square. At the beginning the 15 numbers are mixed (left). You must
order the numbers by sliding (right). |
..  .. .. |
Solution of the
Puzzle top
 |
You don't need special advice to find a solution. Everybody,
who has some patience, can arrange the pieces in the right order.
To get to know the puzzle and to practice, it is best
to build a model. You can move the numbers easily. The pieces don't get
stuck while moving.
You draw a 4x4 square freehand on a piece of cardboard,
cut out 15 suitable cards from paper, label them and lay them on the squares
(left). |
.... .. ..
|
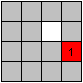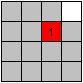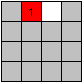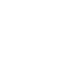
The usual method is moving the numbers from 1 to 15 one
after the other, line after line.
You must not destroy a line. You must keep the order of
the numbers at least. |
... ... ...
|
You start with moving 1 to the left-hand corner above.
Therefore you must make a gap in front of the 1, so that
1 can go forward. You quickly notice, that it is good to take other numbers
with you, too. |
Then the next numbers follow...
... ... ...
|
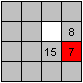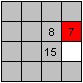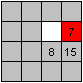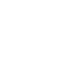
This is a main move, the circle: A number is going around
in a 2x2 square.
Here you can see, how 7 is going to its right place.
If 7 is going around the other way, 8 is also on the right
place. |
... ... ...
|
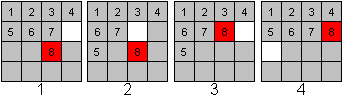
Sometimes you don't have a 2x2 square for moving a piece
(1).
You can see with 8 how to move the incomplete line to
the left and down and then 8 up in a 2x2 square (2,3,4). |
... ... ...
|
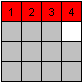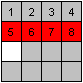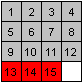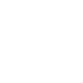
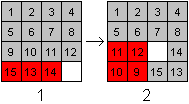
If you have solved the third line, sometimes the fourth
line is also solved and you are finished.
Otherwise the numbers of the last line aren't in the right
order (1).
It is helpful to compress the third line into a 2x2 square
(2). Then it is easy to order the last three numbers 13,14 15. |
...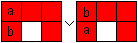 ... ... |
The solution is more systematical, if you know how to
move the pieces inside a 2x3 rectangle.
You always can succeed in moving any two numbers (here
a and b) to the left, also changed (book 09). |
Programs top
...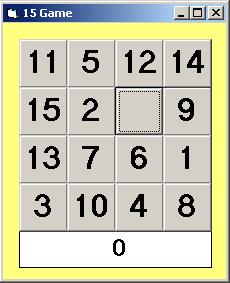 ... ... |
If you have solved the puzzle, your next problem can
be to order it with as few moves as possible.
I have written a small program in Visual Basic V3, which
simulates and counts the moves.
The pieces are already mixed from the start.
You can download the program.
You need Vbrun300.dll. |
There are many programs of the 15 puzzle on the net, especially
one made by Karl Hörnell. You can play them online or offline.
You can also download programs to find out as few moves
as possible. I used Ken'ichiro Takahashi 's program (thanks, URL below)
to solve the pattern on this website. You need at least 59 moves: 9, 1,
6, 9, 1, 14, 12, 1, 2, 15, 11, 5, 1, 2, 15, 7, 9, 4, 10, 3, 13, 9, 3, 10,
8, 6, 14, 15, 4, 3, 7, 11, 5, 1, 2, 4, 3, 8, 6, 14, 15, 12, 4, 3, 8, 6,
14, 15, 12, 8, 6, 7, 11, 6, 7, 11, 10, 14, 15.
The problem of counting the moves of a solution with as
few moves as possible is difficult (12). Today it is known that you can
solve the 15 puzzle with at least 80 moves (12). Thus computers can manage
the huge number of cases.
Some Mathematics
top
Look at a 2x2 square for the sake of simplicity.
Only three pieces are used. The free square is always
at the bottom right-hand corner.
... ... ... |
There are three possibilities under these circumstances
to alter the position of a piece by sliding. You can write them as 123,
312 and 231. |
... ... ... |
You can make 3! = 6 changings (permutations) with three
numbers. There are still the possibilities 132, 213 and 321. They bring
you to the positions of the pieces on the left, which don't appear in the
puzzle. |
How do the permutations differ?
You form all the pairs within the permutations, where
the bigger number is in front of the smaller one (inversions).
top
| permutations:
123
312
231 |
all pairs:
12 13 23
31 32 12
23 21 31 |
inversions:
no pair
2 pairs: 31 32
2 pairs: 21 31 |
These permutations are called even, because the number
of pairs is even.
(The even permutations make the alternate subgroup with
the order 3 of the symmetric group. The basic set must have an order.)
The other permutations are odd:
| permutations:
132
213
321 |
all pairs:
13 12 32
21 23 13
32 31 21 |
inversions:
1 pair: 32
1 pair: 21
3 pairs: 32 31 21 |
top
You can transfer these facts to the 4x4 square.
There are 15 pieces, so you have 15! = 1 307 674 368
000 permutations. Only half of them are even and will appear as positions.
If you also count the empty square, you have 16! = 20
922 789 888 000 possibilities.
Sliding Block Puzzles
top
..... ..... .....
|
I found an insoluble 15puzzle in Italy, where the numbers
14 und 15 are changed.
This puzzle is insoluble. The permutation (1,2,...,13,15,14)
is odd because of the pair (15,14). You can't change it by sliding to the
even permutation (1,2,...,13,14,15). |
I thought that this was intented for making the puzzle insoluble.
Now in August 2004 Martin Beckenkamp sent me an email that a 15puzzle is
installed at his handy [England: mobile (phone), USA: cell (phone) ;-)]
and shows "solved", if the numbers have this order
01 02 03 __
04 05 06 07
08 09 10 11
12 13 14 15
You can reach this order with the Italian puzzle above, where
14 and 15 are changed.
Most 15 puzzles, which you
can buy nowadays, have picture pieces instead of numbers. You must find
the completed picture.
Two examples follow: Ads of Mc Donald's and Kaiser Bier.
 .............. ..............
Hint: You can take off the
tiles with some power. You must slightly lift the middle pieces at the
beginning.
The Eight Puzzle top
...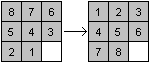 .... .... |
Problem:
Order the numbers going backwards
to the normal order 1 to 8 with a free place on the bottom right. |
Henry Ernest Dudeney invented this
problem. He needed 36 moves. Martin Gardner asked readers of the American
magazine "Scientific American" for solving the puzzle in less steps.
He got many solutions.
... ... ...
|
... ... ...
|
... ... ... |
Result: You only need 30 moves. - There are 10 solutions.
Two solutions (on the left and in the centre) form a pair and are reverse.
You recognize this, if the moves run backwards (on the right). |
... ... ...
|
The corresponding 15 puzzle is insoluble.
But if 1 and 2 change their places, it is soluble. You
need at least 70 moves (Ken'ichiro Takahashi): 2, 5, 9, 13, 14, 10, 11,
7, 3, 1, 6, 11, 10, 15, 7 ,3, 1, 6, 5, 9, 13, 14, 15, 7, 3, 1, 6, 5, 9,
13, 14, 15, 12, 8, 4, 14, 15, 12, 8, 4, 12, 8, 7, 3, 1, 6, 5, 9, 13, 15,
14, 2, 15, 14, 2, 12, 8, 2, 11, 10, 2, 7, 3, 2, 6, 5, 9, 13, 14, 15. |
Sliding
Block Puzzles with Different Tiles top
...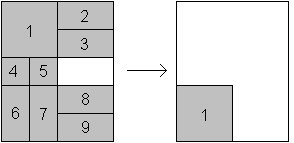 ... ... |
Many puzzles followed the 15 puzzle
in the19th century. You also had to move pieces, but pieces with different
sizes.
You must transport the left top
corner square to the left bottom corner.
You need at least 59 moves (solution
in book 07). |
This sliding block puzzle is called
Dad's Puzzle.
Tower of Babylon
(German: Zauberturm) top
 The "Tower of Babylon" is one of the many puzzles that followed
Rubik's cube. In principle it is a sliding puzzle.
The "Tower of Babylon" is one of the many puzzles that followed
Rubik's cube. In principle it is a sliding puzzle.
You must order 36 balls, so that
there are 6 balls with the same colour in a column and ordered by shades.
You can easily move them horizontally. They are fastened in a ring. Moving
vertically is only possible with a trick: You can push a ball at the bottom
to the middle (left arrow), so it disappears. Then the balls move down
and form a gap at the top (right arrow). If you hold the tower horizontally,
you can move the gap to another place. This is enough to solve the puzzle.
This is a stupid work because of the many balls.
My tower has a screw at the top,
so that I can easily put the tower into pieces and arrange the balls properly
;-). It's a pity I have lost the ball-bearing between the slices :-(.
The 15
Puzzle on the Internet top
German
Gerd Müller
Schiebepuzzle
interaktiv
tan-gram
boss
Wikipedia
15-Puzzle
English
Alexander Bogomolny (cut-the-knot)
Sam
Loyd's Fifteen, History,
Lucky7,
Happy8,
Slider
Don Taylor
The
14-15 Puzzle
Ed Pegg Jr. (MAA online)
sliding-block
Puzzles
Harry Broeders
15puzzle
Herbert Kociemba
Fifteen
Puzzle Optimal Solver
Jaap Scherphuis
14-15
puzzle / Boss puzzle
Jerry Slocum & Dic Sonneveld
The 15 Puzzle
Karl Hörnell's Applet Center
The
15 Puzzle
Nick Baxter
Sliding
Block Home Page
Ken'ichiro Takahashi (takaken)
15Puzzle
Optimal Solver
Wikipedia
Fifteen
puzzle,
Sliding
puzzle
References top
(00) ermann Schubert: Mathematische Mußestunden,
Walter de Gruyter Verlag Berlin 1941 (1.Auflage 1897)
(01) W.Ahrens: Mathematische Unterhaltungen und Spiele,
Leipzig 1918
(02) G.Kowalewski: Mathematica delectans, Band 1 , Leipzig
1921
(03) G.Kowalewski: Alte und neue Spiele, Leipzig 1930
(Nachdruck: Martin Sändig, Walluf 1978 (ISBN
3-500-19830-9)
(04) Martin Gardner: Mathematical Puzzles & Diversions,
New York 1959
(05) Walter Lietzmann: Lustiges und Merkwürdiges
von Zahlen und Formen, Göttingen 1961
(06) Bruno Kerst: Mathematische Spiele, Berlin 1933 (Nachdruck:
Martin Sändig, Wiesbaden 1968)
(07) Martin Gardner: Mathematisches Labyrinth, Braunschweig
1979 (ISBN 3-528-08402-2)
(08) Michael Mrowka: Zauberturm, Teufelstonne und Magische
Pyramide, Niedernhausen/Ts.1981 (ISBN 3-8068-0606-3)
(09) Monika Dewess und Günter Dewess: Summa Summarum,
Thun; Frankfurt am Main, 1986 (ISBN 3-87144-898-2)
(10) Johannes Lehmann (Hrsg.): Rechnen und Raten , Köln
1986 (ISBN 3-7614-0930-3).
(11) L. Edward Hordern: Sliding Piece Puzzles, 249pp,
hb, Oxford, England, 1993, Oxford University Press
(12) F. R. W. Karlemo and P. R. J. Östergård
: On sliding block puzzles, Journal of Combinatorial Mathematics and Combinatorial
Computing 34 (2000), 97-107
(13) Jerry Slocum & Dic Sonneveld: The 15 Puzzle,
Slocum Puzzle Foundation, 257 South Palm Drive, Beverly Hills, CA 90212,
2006
Thank you Gail from Oregon Coast for supporting me
in my translation.
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
2000 Jürgen Köller
top |