|
Was ist ein Quader?
... ... |
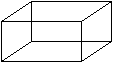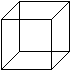
Ein Quader ist ein Körper, der von drei passenden Paaren von
Rechtecken gebildet wird.
Aneinander stoßende Rechtecke stehen senkrecht aufeinander. |
Das ist der gleiche Quader in 3D-Sicht.
Besondere Quader top
Besondere Quader haben auf meiner Homepage eigene Seiten.
Beim quadratischen Prisma sind zwei Seitenflächen Quadrate. Beim
Würfel sind alle Seitenflächen Quadrate.
Beschreibung top
Seitenflächen
... ... |
Die drei Paare von Rechtecken zeigen sich, wenn man den Quader in der
Ebene ausbreitet.
Die Figur ist das Netz des Quaders. |
... ... |
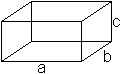Je zwei Rechtecke sind kongruent, so dass nur drei Rechtecke zu beschreiben
sind.
Bezeichnet man die Kanten des Quaders mit a (Länge), b (Breite)
und c (Höhe), so haben die drei Rechtecke die Maße a*b, a*c
und b*c. |
Da Räume oft quaderförmig sind,
bezeichnet man die Flächen eines Quaders auch mit Grundfläche,
Deckfläche, Seitenfläche rechts, Seitenfläche links, Vorderfläche
und Rückfläche.
Kanten
| ...... |
Es gibt 12 Kanten. Vier Kanten haben jeweils dieselbe Länge.
Drei Kanten bilden die Ecke des Quaders und stehen paarweise aufeinander
senkrecht.
Addiert man die Kantenlängen, so ergibt sich die Kantensumme s=4a+4b+4c. |
Eckpunkte
| ...... |
Es gibt 8 Eckpunkte.
Die eulersche Formel für konvexe Körper, f+e=k+2,
wird erfüllt.
Mit f=6, e=8 und k=12 gilt f+e=6+8=14=12+2=k+2. |
Diagonalen
Es gibt 12 Flächendiagonalen. Jeweils vier Diagonalen sind gleich
lang.
Es gibt 4 Raumdiagonalen, die sich in einem Punkt schneiden. Sie sind
gleich lang.
Symmetrie
Der Schnittpunkt der Raumdiagonalen ist der Mittelpunkt
des Quaders und sein Symmetriezentrum.
Es gibt drei Symmetrie-Ebenen und drei Symmetrie-Achsen.
Form
Das Verhältnis der drei Kanten, nämlich a : b :
c, ist geeignet, die Form eines Quaders zu beschreiben.
So hat der auf dieser Seite meist verwendete Quader die Form a:b:c
= 4:3:2 oder a:b:c = 2:1,5:1.
Größen des Quaders top
Der Quader wird i.a. durch die Länge a, die Breite b und die Höhe
c bestimmt.
Daraus lassen sich weitere Größen berechnen.
Volumen V
... ... |
... ... |
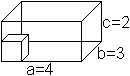
Das Volumen eines Quaders bestimmt man im Anfangsunterricht Geometrie,
indem man einen Einheitswürfel vorgibt und feststellt, wie viele in
den Quader passen. |
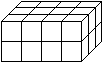
Mit den angegebenen Daten baut man eine Stange aus 4 Würfeln, legt
sie zweimal dahinter und setzt die so entstandene untere Schicht darauf.
Das ergibt V=4*3*2 Einheitswürfel.
Die bekannte Volumenformel V=a*b*c ist nur ein raffiniertes Zählen.
Hier ist V=a*b*c=4cm*3cm*2cm=24cm³.
Oberfläche O
| ... |
Es gilt O=2ab+2ac+2bc.
 |
Diagonalen
... ... |
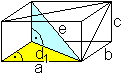Es gibt drei verschiedene Flächendiagonalen.
Nach den Satz des Pythagoras gilt d1=sqrt(a²+b²).
Entsprechend gilt d2=sqrt(a²+c²) und d3=sqrt(b²+c²).
Die Raumdiagonale hat die Länge e=sqrt(d1²+c²)=sqrt(a²+b²+c²). |
Radius der Umkugel
Der Schnittpunkt der Raumdiagonalen hat von den Eckpunkten des Quaders
eine Entfernung, die gleich der halben Länge der Raumdiagonalen ist.
Es gilt also für den Radius der Umkugel R=(1/2)sqrt(a²+b²+c²).
Innenleben eines Quaders top
Mittenkörper
... ... |
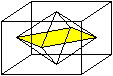Verbindet man die Mittelpunkte der Seitenflächen miteinander,
so entsteht eine Bipyramide.
Die gemeinsame Grundfläche der beiden Pyramiden ist eine Raute.
Ist die Grundfläche des Quaders ein Quadrat, so entsteht eine
quadratische,
gerade Bipyramide. |
Eckpyramiden
... ...
|
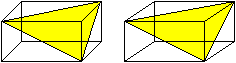
Drei Kanten treffen sich in einem Eckpunkt. Verbindet man die freien
Endpunkte dieser Kanten miteinander, so entsteht eine dreiseitige Pyramide.
Die Seitenflächen sind rechtwinklige Dreiecke, und die drei Flächendiagonalen
bilden die Grundfläche. |
Es entsteht an jedem Eckpunkt eine kongruente Pyramide.
... ...
|
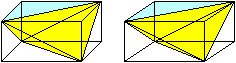
Zwei Pyramiden, die eine Flächendiagonale gemeinsam haben, lassen
unter sich zwei Pyramiden. So wird der Quader in vier kongruente
Pyramiden aufgeteilt. |
... ... |
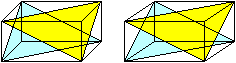Zwei Pyramiden, die zwei gegenüberliegende Ecken besetzen, lassen
zwischen sich eine Art Antiprisma. |
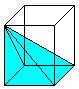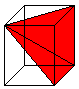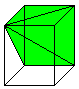
Drei Pyramiden
|
In einem Quader liegen nebeneinander drei volumengleiche, schiefe Pyramiden. |
24 Dreiecke
... ... |
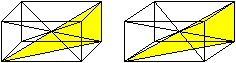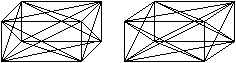
Die Raumdiagonale, eine Flächendiagonale und eine Kante bilden
ein rechtwinkliges Dreieck. Zu jeder Raumdiagonalen gibt es sechs Dreiecke
dieser Art, also gibt es im Quader insgesamt 24 Dreiecke. |
Sechs Rechteck-Pyramiden
... ... |
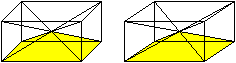Die Seitenfläche des Quaders und sein durch die Raumdiagonalen
festgelegter Mittelpunkt bilden eine Pyramide. Es gibt sechs Pyramiden
dieser Art.
Sie haben das gleiche Volumen. |
Sechs dreiseitige
Pyramiden
... ... |
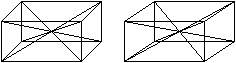
Es gibt sechs schiefe, dreiseitige Pyramiden mit einem halben Rechteck
als Grundfläche und einer Quaderkante als Höhe.
Alle sechs Pyramiden haben das gleiche Volumen.
|
Eine gerade Rechteck-Pyramide
... ... |
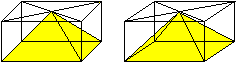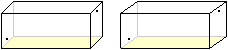
Errichtet man auf der Grundfläche eine gerade Rechteck-Pyramide
und zeichnet die Flächendiagonale der Deckfläche ein, so entstehen
um sie herum vier schiefe Rechteck-Pyramiden. Zwei gegenüberliegende
Pyramiden füllen jeweils ein Drittel des Quaders aus, die gerade Pyramide
auf der Grundfläche das letzte Drittel. |
Pythagoräischer Quader
top
Rechtecke bestehen aus zwei kongruenten, rechtwinkligen Dreiecken.
Es gibt das Problem, einen Quader zu finden, bei dem die soeben beschriebenen
Dreiecke pythagoräisch sind. Das heißt, dass neben den Kanten
des Quaders auch die Flächendiagonalen ganzzahlig sind.
Das Gleichungssystem a²+b²=x², a²+c²=y²
und b²+c²=z² ist also in ganzen Zahlen zu lösen.
In Buch (2) wird eine Lösung von Euler angegeben mit a=240, b=117
und c=44. Das führt zu d1=267, d2=244 und d3=125.
Diese Quader heißen im Englischen folglich Euler Bricks.
Bis heute ist nicht bekannt, ob es auch
ein Zahlentripel gibt, für das zusätzlich die Raumdiagonale e=sqrt(a²+b²+c²)
ganzzahlig ist. (Hier ist e²=73225 oder e=270,6 angenähert.)
Ein solcher Quader würde pythagoräischer Quader heißen.
Es ist leicht, Quader mit ganzzahligen
Kanten zu finden, bei denen nur die Raumdiagonale e= sqrt(a²+b²+c²)
eine ganze Zahl ist.
Bei The On-Line Encyclopedia of Integer Sequences findet man
natürliche Zahlen, die sich als Summe von drei Quadratzahlen >0 schreiben
lassen. Das sind unter 100 die folgenden Zahlen.
3, 6, 9, 11, 12, 14, 17, 18, 19, 21, 22,
24, 26, 27, 29, 30, 33, 34, 35, 36, 38, 41,
42, 43, 44, 45, 46, 48, 49, 50, 51, 53, 54,
56, 57, 59, 61, 62, 65, 66, 67, 68, 69, 70, 72, 73, 74, 75, 76, 77, 78,
81,
82, 83, 84, 86, 88, 89, 90, 91, 93, 94, 96, 97, 98, 99, ...
Darunter sind auch die Quadratzahlen 9, 36, 49 und 81.
Da z.B. 9=1+4+4=1²+2²+2² gilt, hat ein Quader mit a=1,
b=2 und c=2 eine ganzzahlige Diagonale, nämlich e=3.
Puzzles mit Quadern top
Quader bauen
| ...... |
Der Quader 4×3×2 besteht aus 24 Würfeln. Welche Quader
kann man aus ihnen noch bauen?
Es geht dabei um die Zerlegung der Zahl 24 in drei Faktoren:
24=1*1*24=1*2*12=1*3*8=1*4*6=2*2*6=2*3*4. Es gibt also 6 Quader. |
Statt der Einzelwürfel gibt man auch Körper aus mehreren Würfeln
vor, z.B. Tetrawürfel oder Pentominos (s.u.).
Pack Puzzles
... ... |
Es geht dabei darum, in eine Kiste mehrere Holzstücke zu packen,
die sie genau ausfüllen.
In diesem Falle sind es 8 voneinander verschiedene Holzquader.
Puzzles dieser Art können sehr anspruchsvoll sein. |
In Buch (1) werden folgende Pack-Puzzles
beschrieben.
> Der geteilte Block von T.H.O'Beirne
> Das Conway-Packproblem
> Die Haselgrove-Kiste
> Der chinesische Quader
Parallelepiped top
Ersetzt man beim Quader die Rechtecke durch Parallelogramme, entsteht
ein neuer Körper, das Parallelepiped.
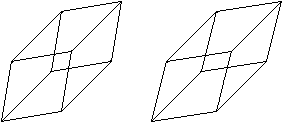
Der Kalkspat kann diese Form annehmen, deshalb heißt der Körper
auch Spat.
... ... |
Das hat mich in vielen Souvenir Shops in den USA begeistert.
Neben dem üblichen Touristenzeug gab es lehrreiche und preiswerte
Mitbringsel aus den Naturwissenschaften und der Geologie. Diesen Kalkspat
kaufte ich 1996 für einen Dollar in Ruby's Inn am Eingang zum Brice
Canyon.
Der Stein hat sich bis heute (2010) nicht verändert. |
Quader um uns top
Hier ist eine kleine, persönliche Auswahl.
A4-Blatt Druckerpapier 80g/m²
Streichholzschachtel
9-V-Block
250g abgepackte Butter
Backstein, Normalformat (NF) - Deutschland
20'-Standardcontainer, außen
Bramme auf der Schurenbachhalde in Altenessen
UN Hauptgebäude in New York |
210mm × 297mm × 0,1mm
5,0cm × 3,5cm × 1,5cm
48,5 mm × 26,2 mm × 17 mm
10cm × 7,5cm × 3,4cm (gemessen)
24,0cm × 11,5cm × 7,1cm
6,1m × 2,4m × 2,6m
14,5m × 4,2m × 13,5cm (67 Tonnen schwer)
91m × 22m × 154m (geschätzt nach google map, o.G.) |
6,23cm³
26,2cm³
216cm³
255cm³
1,96dm³
38 m³
822m³
sinnlos |
Quelle der meisten Daten: Wikipedia
Auch an anderen Stellen meiner Webseite
kommen Quader vor.
Fliege-Spinne-Problem
Quader aus Pentawürfel
... ... |
Es gibt etliche Quader, die man aus allen 12 Pentomino-Steinen bauen
kann.
Mehr findet man unter Quader
aus Pentawürfeln. |
Quader aus Tetrawürfeln
... ... |
Es gibt etliche Quader, die man aus allen 12 Tetrawürfeln bauen
kann.
Mehr findet man unter Quader
aus Tetrawürfeln. |
Kasten
... ... |
Einen oben offenen Kasten
bastelt man aus einem quadratischen Blatt Papier. |
Quader im Internet top
Deutsch
Susanne Prediger
Quader
bauen aus 24 Würfeln – Kinder auf dem Weg zur Volumenformel
(.pdf Datei)
mathepower.com
Quader
Wikipedia
Quader, Parallelepiped,
Rhomboeder
Englisch
Danail Obreschkow, Nick Jones, Neil Johnson (University of Oxford)
Broken Symmetry
and the Magic of Irregular Dice
Eric W. Weisstein
Cuboid, Hyperrectangle,
Euler
Brick,
Perfect
Cuboid, Parallelepiped
Fred Curtis
Primitive
Euler Bricks
Gijs Korthals Altes
Paper
Model of a Rectangular Prism, Paper
Model of a Oblique Rhombic Prism
Parallelepiped,
Rob Stegmann (Rob's Puzzle Page)
3-D
Packing Puzzles with Identical or Similar Pieces
The On-Line Encyclopedia
of Integer Sequences
Numbers that are the sum of 3 nonzero squares: A000408
Wikipedia
Cuboid, Euler
brick, Parallelepiped,
Unit
block
Referenzen top
(1) Pieter van Delft, Jack Botermans: Denkspiele der Welt, München
1998 ISBN 3-88034-87-0]
(2) David E. Hayes and Tatiana Shubin (Editors): Mathematical Adventures
for Students and Amateurs (Google book)
Das Kapitel Pythagorean
Cuboids (page 61/ 62) steht im Internet zur Verfügung.
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
http://www.mathematische-basteleien.de/
©
2010 Jürgen Köller
top |
...