Was ist eine Potenzzahl?
Zahlenbeispiel
Im Englischen heißen die Potenzzahlen Perfect Powers und im Deutschen auch - vielleicht in Anlehnung an die englische Bezeichnung - Perfekte Potenzen. Auf dieser Webseite habe ich das zusammengestellt, was ich zu Potenzzahlen interessant fand. Die Potenzzahlen bis 1000 top
Zu der Anzahl A=41 bis 1000 gelangt man auch über die Potenzen mit einer Primzahl als Hochzahl.
Addiert man die Potenzen, so gelangt man zu der zu großen Summe 42. Das liegt daran, dass man die Potenzen 8^2 = 4^3 und 27^2 = 9^3 doppelt gezählt hat. Also ist die Summe 40. Berücksichtigt man noch die Eins, erhält man die Anzahl 41, was zu zeigen war. Hinter dieser Methode steht das Einschluss-Ausschluss-Verfahren, eine Methode aus der Mengenlehre. Für zwei Mengen heißt die Formel: Danach ist die Anzahl der Potenzen bis 1000 ohne Eins A(2)+A(3)+A(5)+A(7)-A(2*3) = 30+9+2+1-2 = 40. Näheres zum Prinzip von Inklusion und Exklusion findet man auf der Seite von de.wikipedia (URL unten). (Anmerkung von Torsten Sillke) Für die Anzahl der Potenzzahlen bis 10^n gibt OEIS unter http://oeis.org/A070428 an: 1, 4, 13, 41, 125, 367, 1111, 3395, 10491, 32670, ... Umwandlungen top
Von der Potenzzahl zur Potenz Das wird am Beispiel 1.157.625 erklärt. > Man zerlegt die Zahl in Primfaktoren, wobei die Teilbarkeitsregeln hilfreich sind, 1157625 = 33*53*73. Es gilt nach einem Potenzgesetz 33*53*73= (3*5*7)3 und somit ist 1.157.625 = 1053. > Steht ein Taschenrechner zur Verfügung, so kann man die Hoffnung haben, dass die Hochzahl klein ist. Man gibt in den TR [1157625 yx (1/n)] (n=2,3,4,...) ein und stellt bei dieser Zahl erfreut fest, dass schon [1157625 yx (1/3)] eine Potenzzahl ist, nämlich 105. Besondere Potenzen
top
Dazu kommen noch (bis 1000) die 17*10-2 = 168 Primzahlen
selbst mit der Hochzahl 1.
Das bedeutet, dass bis 1000 16,8% der Zahlen Primzahlen sind und 19,3% Primzahlpotenzen. Quadratzahlen haben die Hochzahl 2.
Kubikzahlen haben die Hochzahl 3.
Mehr auf meiner Webseite Kubikzahlen Zweierpotenzen haben die Grundzahl 2.
Große Zahlen top
Als Beispiel einer großen Zahl habe ich nicht zufällig die Zahl 10^100 ausgewählt. Der amerikanische Mathematiker Edward Kasner prägte für sie 1920 den Namen Googol, der populär geworden ist und der es zu einer eigenen Wikipedia-Seite gebracht hat (URL unten). Nach der Seite https://en.wikipedia.org/wiki/Google_(verb)#Etymology ist daraus nicht der Name der Suchmaschine Google hervorgegangen, was eigentlich naheliegend wäre. Dr. Francis Googol, great-great-great-grandson of Francis Drake, in Buch (1) geht (natürlich) auf die Zahl Googol zurück. Man benennt große Zahlen mit Tausend, Million, Milliarde, Billion und Billiarde. Dabei ist jede dieser Zahlen um den Faktor 1000 größer als die vorherige. Man hat nicht das Bedürfnis, sich auf noch größere Zahlen einzulassen, einfach, weil sie unanschaulich werden und weil sie im praktischen Leben kaum vorkommen. Immerhin hat 1 Billiarde nach der Eins schon 15 Nullen. Meinetwegen, man hat sich Namen für noch größere Zahlen überlegt. Auf der Webseite Zahlennamen von Wikipedia (URL unten) wird ein Schema mit Namen noch größerer Zahlen vorgestellt. Die größte Zahl auf der Webseite ist 1 Duzentilliarden = 10^1203. Dummerweise gibt es in der englischsprachigen Welt für große Zahlen andere Namen. Im Amerikanischen (genauer in U.S., English Canada, Australia, and modern British) heißt die Reihe Thousand, Million, Billion, Trillion und Quadrillion. Mir gefällt, dass man einer nicht näher definierten, sehr großen Fantasiezahl den Namen eine Zillion gegeben hat. Potenzen
mit dem Taschenrechner top
Größere Zahlen als 9.999.999.999 werden im Rechner auch angezeigt, dann aber in der Exponentialform oder wissenschaftlichen Form und dann oft gerundet. Berechnet man eine Potenz mit [10 yx 99 =], so wird das Ergebnis mit der Eins vorne und den folgenden 99 Nullen dargestellt als 1.99, zu verstehen als 1099. Gibt man [10 yx 100 =] ein, so erscheint im Display Error. Die Zahl ist für den Taschenrechner zu groß. Der Exponent darf nur ein- oder zweistellig sein. In der wissenschaftlichen Darstellung werden Zahlen durch eine Dezimalzahl (oder Mantisse) und einen Exponenten angegeben. Soll z.B. die Zahl 1234 in der wissenschaftlichen Form angezeigt werden, drückt man [2nd SCI 1234 =]. Dann erscheint 1.234 03, zu verstehen als 1,234*103. - Die übliche Darstellung wird reaktiviert mit 2nd FLO. Will man eine Zahl, die in der wissenschaftlichen Form vorliegt, eingeben, tippt man nacheinander die Mantisse, und den Exponenten ein, getrennt von der Taste EE. Für die Eingabe von 1,234*103 drückt man [1.234 EE 3]. Mit [2nd FLO] gelangt man in die übliche Darstellung. Die Mantisse ist eine Dezimalzahl und kann bis zu 9 Dezimalen
haben. Will man die Zahl 1.123456789 03 auf 2 Stellen genau
angeben, gibt man noch [2nd Fix 2] ein. Es erscheint 1123.46.
Große Primzahlen
top
Potenzen
als Stufenzahlen top
Zweierpotenzen als Stufenzahlen Man kann z.B. die Zahl 39=3*10+9 auch im Zweiersystem darstellen. Dazu zerlegt man sie in eine Summe aus Zweierpotenzen (39 = 1+2+4+32) und kennzeichnet die vorkommenden Zweierpotenzen in einer Tabelle durch eine Eins.
Die Zweierpotenzen heißen Stufenzahlen so wie die Zehnerpotenzen im Dezimalsystem. Mehr auf meiner Seite Zweiersystem Teilmengen
einer Menge top
Gegeben ist die Menge M = {a,b,c,d} aus vier Elementen.
Verallgemeinerung Satz: Eine Menge von n Elementen hat 2n Teilmengen. Beweis dieser Aussage durch vollständige Induktion
Bemerkung
zu den Potenzen a^1 und a^0 top
Setzt man a=0, so gilt 01= 0 und 00 = 0. Somit haben zwei Potenzen mit gleicher Grundzahl denselben gleichen Wert 0. Man löst diesen Widerspruch auf, indem man 01= 0 festlegt und 00 nicht definiert. So zeigt auch der TI-30Xa Solar nach Eingabe von [0 yx 0=] im Display Error.
Sucht man bei Google mit "x hoch x grenzwert", gelangt man zu mehreren Beweisen zu lim(x^x) = 1 für x gegen +0. Summe von Potenzen
top
Geometrische Reihe Die Summe sn = a + aq + aq² + aq³ + ...+ aqn-1 ist bekannt als geometrische Reihe. Dabei stehen die Variablen a und q für relle Zahlen, q sollte nicht gleich Null sein. Die Summe fasst man zusammen zu sn = a(1-qn)/(1-q). Beispiel: 20+21+22+20 + ...+210=2*(1-29)(-1) = 511 Mehr auf meiner Webseite Geometrische Folgen und Reihen Summen mit gleichen Hochzahlen Es geht um die Summen 1k+2k+3k+...+nk. Dabei ist k eine natürliche Zahl. Für k = 1 ergeben sich die Dreieckszahlen 11+21+31+...+n1 = 1+2+3+...+n = (1/2)n(n+1) = (1/2)n2+(1/2)n. Mehr auf meiner Webseite Dreieckszahlen. Für k=2 ergibt sich die Summe der Quadratzahlen 12+22+32+...+n2 = (1/6)(n+1)(2n+1) = (1/3)n3+(1/2)n2+(1/6)n. Man benötigt die Formel bei der Berechnung der Fläche unter der Parabel nach der Streifenmethode. Die Formel wird nach der Methode der vollständigen Induktion bewiesen werden. Beweis Die Formel gilt für n=1: 1² = (/1/2)*1*(1+1) Angenommen, sie gilt für n: 12+22+32+...+n2 = (1/6)n(n+1)(2n+1) Dann ist zu zeigen, dass sie auch für n+1 gilt. D.h. 12+22+32+...+n2+(n+1)2= (1/6)(n+1)(n+2)[2(n+1)+1]. Es ist also <=> (1/6)[n(n+1)(2n+1)+6(n+1)²] = (1/6)(n+1)(n+2)(2n+3) |*6 <=> [n(n+1)(2n+1)+6(n+1)²] = (n+1)(n+2)(2n+3) <=> n(2n²+n+2n+1)+6n²+12n+6 = (n+1)(2n²+3n+4n+6) <=> 2n³+3n²+n+6n²+12n+6 = 2n³+7n²++6n+2n²+3n+4n+6 <=> 2n³+9n²+13n+6 = 2n³+9n²+13n²+6 Mehr auf meiner Webseite Parabel/Flächenproblem Mehr auf meiner Webseite Kubikzahlen/Folgen und Reihen. Dort findet man einen Beweis der Formel. Die faulhabersche Formel ist eine Verallgenmeinerung und gibt die Summe der ersten Potenzen durch ein Polynom an. Die Formel lautet 1k+2k+3k+...+nk = Pk+1(n). Dabei ist Pk+1(n) ein Polynom in n. Die Koeffizienten enthalten die Bernoullizahlen. Mehr auf der Wikipedia-Seite "Faulhabersche Formel" (URL unten) Vier-Quadrate-Satz Die Behauptung ist: "Jede natürliche Zahl kann als Summe von vier Quadratzahlen geschrieben werden." Es gibt nicht unbedingt nur eine Darstellung. Zahlenbeispiele: 54 = 2^2+3^2+4^2+5^2, 13 = 3^2+2^2+1^2+0^2, 13 = 1^2+2^2+2^2+2^2 Der Satz wurde 1770 von Lagrange bewiesen. Wikipedia: https://de.wikipedia.org/wiki/Vier-Quadrate-Satz https://en.wikipedia.org/wiki/Lagrange%27s_four-square_theorem Waringsche Problem Zu jeder natürlichen Zahl gibt es einen Exponenten k, so dass sie als Summe von g k-ten Potenzen dargestellt werden kann. Dabei soll g minimal ist. Speziell gilt: Jede Zahl ist die Summe von vier Quadratzahlen (Vier-Quadrate-Satz) Jede Zahl ist die Summe von höchstens 9 Kubikzahlen. Jede Zahl ist die Summe von höchstens 19 Biquadraten Der Satz ist gelöst. https://de.wikipedia.org/wiki/Waringsches_Problem https://en.wikipedia.org/wiki/Waring's_problem Pythagoreisches Tripel Die Gleichung x2+y2 = z2 hat für natürliche Zahlen x,y,z unendlich viele Lösungen. Beispiel: (x,y,z) = (3,4,5) https://de.wikipedia.org/wiki/Pythagoreisches_Tripel https://en.wikipedia.org/wiki/Pythagorean_triple Mehr auch auf meiner Webseite Darstellung pythagoräischer Zahlen Großer Fermatscher Satz (Englisch: Fermat's last Theorem) Die Gleichung xn+yn = zn hat für natürliche Zahlen x, y, z für jedes n>2 keine Lösung. https://de.wikipedia.org/wiki/Gro%C3%9Fer_Fermatscher_Satz https://en.m.wikipedia.org/wiki/Fermat%27s_Last_Theorem Jacobi–Madden equation Die Gleichng a4+b4+c4+d4 = (a+b+c+d)4 hat unendlich viele Lösungen. Beispiel: 353^4 = 30^4 + 120^4 + 272^4 + 315^4. https://en.m.wikipedia.org/wiki/Jacobi%E2%80%93Madden_equation
Zahlenspielereien top Eine Gleichung
Catalansche Vermutung Die Gleichung xp-yq =1 in ganzen Zahlen wird nur gelöst durch 32-23 =1. 666 Es gibt auch Darstellungen in Potenzen der bekannten Zahl 666 der Zahlenmystik.
(1) Mehr auf meiner Webseite Römische
Ziffern
Apocalyptic Number Die Zahl 2^157 ist eine apokalyptische Zahl, denn sie enthält die Ziffernfolge 666. Potenzen und Quersumme
Näheres auf meiner Webseite Quersumme Potenzzahlen im Internet top Deutsch HELMUT RICHTER, BERNHARD SCHIEKEL
K. P. RYBAKOWSKI
M. Rheinländer (Universität Konstanz)
Wikipedia
Englisch Eric W. Weisstein (MathWorld)
Jean-Charles Meyrignac
OEIS (The On-Line Encyclopedia of Integer Sequences)
Wikipedia
Referenzen top
URL meiner Homepage:
© Februar 2017 Jürgen Köller |
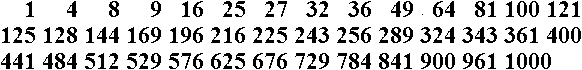 ...
... ...
... ...
... ...
...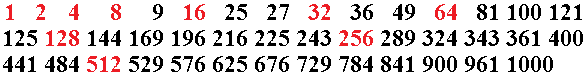 ...
... ...
...
 ...
...