|
Was sind Dreieckszahlen?
Das sind die ersten 100 Dreieckszahlen:
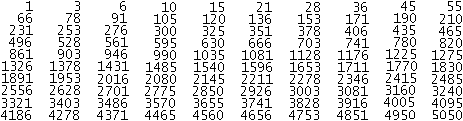
Die Folge der Dreieckszahlen entsteht aus den natürlichen
Zahlen.
Man gibt 1 vor und addiert nacheinander die nachfolgende
Zahl:
1
1+2=3
(1+2)+3=6
(1+2+3)+4=10
(1+2+3+4)+5=15
...
Der Name Dreieckszahl erklärt
sich aus der folgenden graphischen Darstellung.
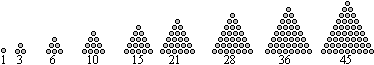
Formeln top
Die allgemeine Darstellung einer Dreieckzahl ist dn=
1 + 2 + 3 + 4 +...+ (n-2) + (n-1) + n,
wobei n eine natürliche Zahl ist.
Diese Summe kann man mit dn=
n * (n + 1) / 2 zusammenfassen.
Beweis:
dn= 1
+ 2 + 3 + ...+ (n-2) + (n-1) + n
dn= n
+ (n-1) + (n-2) +... + 3 + 2 + 1
------------------------------------------
Die Terme auf beiden Seiten werden addiert.
Dabei werden die rechten Terme
paarweise zu (n + 1) zusammengefasst. Es gibt n Terme.
2dn=n * (n+1)
dn= n * (n + 1) / 2, w.z.b.w.
Es gilt die Rekursionsformel d1=1
und dn+1= dn+ n
Besondere Dreieckszahlen
top
Gerade und ungerade Dreieckszahlen
... ... ... |
Man sieht:
Die geraden Dreieckszahlen in Rot und die ungeraden in
Schwarz bilden in der normalen Reihenfolge Paare. |
Die kleinsten Quadratzahlen
1=1²
d8=36=6²
d49=1225=35²
d288=41616=204²
d1681=1413721=1198²
d9800=480024900=6930²
d57121=1631432881=40391²
...
|
Die kleinsten Palindrome
d10=55
d11=66
d18==171
d34=595
d36=666
d77=3003
d109, d132, d173 , d363,
...
|
Vollkommene Zahlen
Eine Zahl, deren Summe ihrer Teiler
(kleiner als die Zahl selbst) gleich der Zahl ist, heißt vollkommene
Zahl.
Die ersten vollkommenen Zahlen
sind 6, 28 und 496. Sie sind Dreieckszahlen wie jede vollkommene
Zahl.
Die Zahl 666
Die Summe aus sechs der sieben römischen Ziffern
ist D+C+L+X+V+I=666. Das Zeichen M fehlt.
Man kann auch schreiben: DCLXVI=666.
666 ist die größte Dreieckszahl,
die man aus gleichen Ziffern bilden kann. Das ist bewiesen (1, Seite 98).
666 ist eine Smith-Zahl. Das heißt:
Die Quersumme [6+6+6] ist gleich der Summe der Ziffern aller Primteiler
[2+3+3+(3+7)]
(1, page 200).
Die Zahl 666 geriet ins Zwielicht,
weil sie in der Bibel als "Zahl des Tieres" bezeichnet wird:
Hier ist Weisheit! Wer Verstand hat, der überlege
die Zahl des Tieres; denn es ist eines Menschen Zahl, und seine Zahl ist
sechshundertsechsundsechzig
(Offenbarung des Johannes 13,18 in Luthers
Übersetzung).
In der Interpretation der Bibelausleger ist die Zahl
des Tieres eine "böse Zahl" und wird auch als Zahl des Biestes (Number
of the Beast), als Satanszahl oder als Zahl des Antichristen bezeichnet.
Folglich hat man 666 in den Namen der Kaiser Nero und
Diokletian gesucht und gefunden, denn sie haben in ihrer Zeit die Christen
verfolgt.
Zur Zeit der Religionskriege im 16.Jahrhundert wurde
666 mit dem Namen Luthers verbunden, im Gegenzug auch mit dem des Papstes.
Das Beispiel des Papstes verfolgt das Prinzip der Chronogramme.
Der Papst wird bezeichnet mit VICARIUS FILII DEI (Stellvertreter
des Sohnes Gottes). Addiert man darin die Werte der römischen Ziffern,
so ergibt sich 666 (VICARIVS FILII DEI).
Im Internet wird man nach Eingabe des Suchwortes 666 überschwemmt
mit Informationen, wenn man denn will.
Paare zählen
top
Gibt man z.B. 5 Objekte vor wie die Buchstaben a,b,c,d
und e, so kann man nach der Anzahl der Paare fragen, die man aus ihnen
bilden kann.
In diesem Falle sind das die zehn Paare ab, ac, ad, ae,
bc, bd, be, cd, ce und de. Die Anzahl ist die Dreieckszahl 1+2+3+4.
Dieser Sachverhalt hat viele Anwendungen. Hier vier Beispiele:
Dominosteine
Gegeben sind je 8 gleiche Quadrate mit den Augen 0,1,2,3,4,5
und 6. Sie werden zu Paaren zusammengestellt.
 Es gibt 7+6+5++4+3+2+1=28 Steine. Das ist eine Dreieckszahl.
Es gibt 7+6+5++4+3+2+1=28 Steine. Das ist eine Dreieckszahl.
...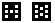 ... ...
|
Es gibt auch Dominospiele mit 36 oder 45 Steinen, wenn
man Quadrate mit 7 und 8 Augen hinzufügt. |
Jeder mit jedem
...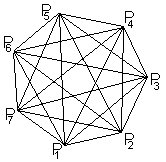 ... ... |
Verbindet man n Punkte mit allen möglichen geraden
Linien, so ergeben sich 1+2+3+...+(n-1) Strecken.
Links ein Beispiel für n=7. |
Hände
schütteln
Bei einer Gesellschaft mit n Personen schüttelt
jeder jedem die Hand.
Ergebnis: Man gibt sich [1+2+3+...+(n-1)]- mal die Hand.
Prost
Jeder stößt mit jedem mit einem Glas Sekt
an.
Anzahl
der Rechtecke im nxn-Quadrat
... ... ...
|
Im 3x3-Quadrat links gibt es 36 Rechtecke, davon sind
14 Rechtecke sogar quadratisch. |
Begründung für ein nxn-Quadrat:
Jedes Rechteck wird aus Paaren zweier Vertikalen und
zweier Horizontalen gebildet.
Es gibt n+1Vertikale, aus denen man n(n+1)/2 Paare bilden
kann. n+1 Horizontale haben auch n(n+1)/2 Paare.
Insgesamt gibt es [n(n+1)/2]² Kombinationen.
Setzt man n=3, ergibt sich 36.
Man kann leicht auf die Anzahl von Quadern im Würfel
und sogar in einem Quader verallgemeinern.
(Andreas Künkenrenken, danke für die Zuschrift.)
Gaußsche
Summenformel top
Vom bedeutenden Mathematiker Karl Friedrich Gauß
(1777-1855) erzählt man sich die folgende Geschichte:
Er sollte als Schüler in der Schule die Zahlen von
1 bis 100 zusammenzählen. Der Lehrer nahm an, dass er damit eine Weile
beschäftigt war. Schon nach kurzer Zeit fand er die Summe 5050.
Erklärung:
Statt stur die Zahlen von 1 bis 100 der Reihe nach zu
addieren, bildete er Zahlenpaare mit denselben Summenwerten und konnte
multiplizieren:
1+2+3+4+...+50+51+...+99+100
= (1+100) + (2+99) + ... + (50+51)
= 50*101
= 5050
[(3), Seite 22f.]

Lage im Pascalschen
Dreieck
top
...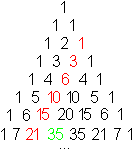 ... ...
|
Wie so oft in der Zahlentheorie bietet auch hier das
Pascaldreieck
einen Beitrag:
Die rot gekennzeichneten Zahlen sind Dreieckszahlen.
Man kann im Dreieck auch die Summe der Dreieckszahlen
ablesen.
Beispiel: 1+3+6+10+15=35 |
Damit lassen sich die Dreieckszahlen auch als Binomialkoeffizienten
darstellen.

Figurenzahlen
top
Die Dreieckszahlen können verallgemeinert werden.
Man erweitert auf Vierecke, Fünfecke usw.
Dreieckszahlen
Quadratzahlen
Fünfeckszahlen
Sechseckszahlen
Siebeneckszahlen
Achteckszahlen
...
|
n*(n+1)/2
n²
n*(3n-1)/2
n*(4n-2)/2
n*(5n-3)/2
n*(3n-2)
...
|
1 3 6 10 15 21 28...
1 4 9 16 25 36 49...
1 5 12 22 35 51 70...
1 6 15 28 45 66 91...
1 7 18 34 55 81 112...
1 8 21 40 65 96 133...
...
|
Eine Spielerei ist es herauszufinden, welche Dreieckszahlen
in den neuen Zahlenfolgen vorkommen.
Man kann in einer Verallgemeinerung
der Dimension 2 (Dreieckszahlen) auf höhere Dimensionen ausdehnen:
Dreieckszahlen
Tetraederzahlen
Hypertetraederzahlen
...
|
n*(n+1)/2
n*(n+1)*(n+2)/6
n*(n+1)*(n+2)*(n+3)/24
...
|
1 3 6 10 15 21...
1 4 10 20 35 56...
1 5 15 35 70 126...
...
|
Auch hier stellt sich die Frage, welche Dreieckszahlen sich
in höheren Dimensionen wiederholen.
Es gilt der Satz: Die Summe
zweier aufeinanderfolgender Dreieckszahlen ist eine Quadratzahl.
Zum Beweis rechnet man dn + dn+1
aus und erhält (n+1)².
Auch die Darstellung mit Dreiecken oben bestätigt
diese Aussage.
Zahlenfiguren
top
Die folgende Spielerei findet man auf meiner Seite Fakultäten.
5
7 9
7 1 2
6 0 2 0
7 4 7 3 6
7 9 8 5 8 7
9 7 3 4 2 3 1
5 7 8 1 0 9 1 0
5 4 1 2 3 5 7 2 4
4 7 3 1 6 2 5 9 5 8
7 4 5 8 6 5 0 4 9 7 1
6 3 9 0 1 7 9 6 9 3
8 9 2 0 5 6 2 5 6
1 8 4 5 3 4 2 4
9 7 4 5 9 4 0
4 8 0 0 0 0
0 0 0 0 0
0 0 0 0
0 0 0
0 0
0
|
Die Zahl 81! hat 121 Ziffern.
Diese Anzahl ist die Summe der Dreieckszahlen d10+d11=55+66.
Deshalb kann man eine Figur aus zwei Dreiecken bilden. |
8 2 4 7 6 5
0 5 9 2 0 8 2
4 7 0 6 6 6 7 2
3 1 7 0 3 0 6 7 8
5 4 9 6 2 5 2 1 8 6
2 5 8 5 5 1 3 4 5 4 3
7 4 9 2 9 2 2 1 2 3
1 3 4 3 8 8 9 5 5
7 7 4 9 7 6 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0
|
Die Zahl 65! hat 91 Ziffern.
Aus ihnen bildet man ein Sechseck.
Es gilt (d10+d11)- 2*d5=55+66-2*15=91 |
Dreieckszahlen
im Internet top
Deutsch
blogger.de
153
Jutta Gut
Figurierte
Zahlen - die Arithmetik der Spielsteinchen
Wikipedia
Dreieckszahl,
Zentrierte
Dreieckszahl, Polygonalzahl,
Sechshundertsechsundsechzig,
Hundertdreiundfünfzig,
Gaußsche
Summenformel
Englisch
Alexander Bogomolny (cut-the-knot)
There
exist triangular numbers that are also square
Bit-Player
Versions
of the Gauss Schoolroom Anecdote
Eric W. Weisstein (MathWorld)
Triangular
Number (Figurate
Number, Heptagonal
Triangular Number, Octagonal
Triangular Number,
Pentagonal
Triangular Number, Pronic
Number, Square
Triangular Number)
Mathpages.com
Square
Triangular Numbers
Patrick De Geest (World of Numbers)
Palindromic
Triangulars
Peter Macinnis
Enquiring
into triangular numbers
Shyam Sunder Gupta
Fascinating
Triangular Numbers
Wikipedia
Triangular
number, Centered
triangular number, Polygonal
number, 153
(number), 666
(number)
Referenzen top
(1) Martin Gardner: Die magischen Zahlen des Dr. Matrix,
Frankfurt am Main 1987 [ISBN 3-8105-0713-X]
(2) Jan Gullberg: Mathematics - From the Birth of Numbers,
New York / London (1997) [ISBN 0-393-04002-X]
(3) Walter Lietzmann: Lustiges und Merkwürdiges
von Zahlen und Formen, Göttingen 1969
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2003 Jürgen Köller
top |
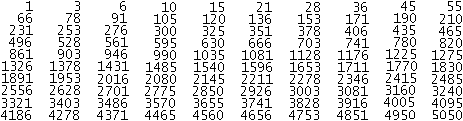
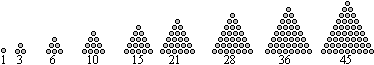

 ...
... ...
...
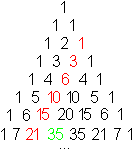 ...
...